(Note on movies: movies are best viewed by advancing one frame at a time using the right or left arrows on the keyboard or movie progress bar. Internet Explorer may not be able to do this and/or it may hide the progress bar. If so, you can double click the movie and it will play, but you will not be able to view frame by frame.)
(Note on presentation: this article is not "light reading" and is meant to be an important contribution to the research literature on spin generation in tennis [literature that is usually not available without paying a download fee from a scientific journal or organization]. Nonetheless, features have been added throughout to make for easier, more engaging, and fun(?) exploration. All the math can be made to disappear with a click of a button and many movies have been added that say it all with pictures. However, just is case this is not your cup of tea, here is a less rigorous presentation of spin and string movement.)
Abstract
Experiments were conducted to compare the spin generated by 16 different tennis strings, using both clamped and hand-held racquets. The ball was incident with backspin at speeds around 23 m/s (51 mph), at an angle of incidence of 40° away from the normal. It was found that (a) the outgoing ball spin is more sensitive to small changes in incoming ball parameters than it is to small changes in string properties, (b) polyester strings generate more spin than nylon strings and (c) the outgoing ball spin decreases by about 30% when the racquet is hand-held. Results are also presented for a few, selected strings where the ball was incident without spin on both clamped and hand-held racquets.
I. INTRODUCTION
Tennis players have claimed for many years, on the basis of their own on-court experience, that some tennis strings generate more spin than others. However, there is only limited information available to quantify the effect. In 2006, the ITF (International Tennis Federation) conducted tests on a number of strings, and found that polyester strings tend to generate slightly more spin than nylon strings.1 A larger sample of strings was tested by the ITF in 20072, showing that the rebound spin can vary from about 1100 rpm to about 1900 rpm when the ball is incident on a clamped racquet at 25 m/s, at 40° to the normal and with 4000 rpm of backspin. We describe in this paper a similar set of measurements to those reported by the ITF, and include additional information on (a) the sensitivity of such measurements to small variations in the incident ball speed, spin and angle, (b) differences that arise when the string tension is varied and when the racquet is hand-held, and (c) some interesting results when the ball is incident without spin or off-axis.
Ideally, an experiment to measure ball spin off a racquet would be conducted under actual playing conditions. However, there is normally a wide variation in the incoming ball speed, spin and angle, as well as a wide variation in racquet head speed and trajectory under actual playing conditions. As a result, differences in ball spin due to different racquet strings would almost certainly be masked by these other variations. It is for that reason that reliable measurements of differences in ball spin need to be undertaken under controlled conditions where the incoming ball parameters are held relatively constant, and where the racquet head speed is held constant. In fact, there is no need to swing the racquet at all, since impacts of this type can be studied in a reference frame where the racquet head is initially at rest. For example, the ITF chose to clamp the racquet head to a rigid frame for convenience, in order to determine the variation in rebound spin from different strings.
Our own experiments were conducted using both clamped and hand-held racquets, the most extensive set of data being obtained with clamped racquets. We attempted to keep the incoming ball speed, spin and angle all constant, but the ball launcher we chose to use was not specifically designed for this purpose, with the result that variations in the incoming ball parameters tended to mask small differences in outgoing ball spin off different strings. Consequently, additional experiments were undertaken to measure changes in outgoing ball spin as functions of the incoming ball parameters. The data from the additional experiments were then used, in conjunction with a theoretical model of the bounce process, to normalize all outgoing ball spin data to the same incoming ball parameters.
II. EXPERIMENTAL DETAILS
Sixteen different strings were tested in this experiment, 15 of them strung in 15 nominally identical Head Extreme Pro Mid Plus racquets. The 15 strings were strung at specified tensions (either 52 lb or 62 lb) a few days before the tests. The 16th string (nylon) was mounted in a similar size racquet head and was strung about four years before testing. The latter string was tested to determine whether an "old" string performed any better or worse than a "new" string in terms of the outgoing ball spin. The string tension in each racquet was measured a few hours before the tests commenced, using an ERT 700 dynamic string tester. The strings are listed in Table 1, and were all 16 gauge. The ERT reading is lower than the nominal tension at which the racquets were strung, since string tension drops quickly immediately after a racquet is strung and then slowly over the next few days.3
The strings were tested by assembling apparatus on a tennis court for convenience, and so that high speed filming, at 300 fps or 600 fps, could be conducted in sunlight. Each racquet was clamped, in turn, in a vertical orientation to a 10 kg aluminum frame mounted on the court, as shown in Fig. 1. Balls were projected from a Tennis Tutor ball machine in a horizontal direction to impact the center of the strings at a speed of 23 ± 2 m/s and at an angle of incidence of 41 ± 2° to the normal. The balls were projected with backspin, mostly at spin rates in the range 400 ± 20 rad/s, although balls were occasionally projected at spins as low as 350 rad/s and as high as 450 rad/s. The data from the high and low backspin balls could have been discarded, but were analysed and included in the final data set using the normalization procedure described in Section IV.

Fig. 1. Arrangement used to film the bounce of a ball incident at 40° on a clamped racquet. The racquet was mounted vertically (clamped as shown or hand-held) and the ball was projected horizontally to impact the center of the strings.
Each bounce was filmed by mounting a Casio EX-F1 video camera on an extension arm attached to a tripod so that the camera pointed vertically downward to a point about 20 cm in front of the strings. In that manner, the camera viewed the trajectory of the incoming and outgoing ball in the horizontal plane, at right angles to that plane. The bounce was filmed at 300 fps with an exposure time set to 1/4000 sec to minimize blurring of the image of the ball in each frame.
A line was drawn around the equator of each ball, and each ball was fed by hand into the ball machine so that the line could be viewed by the camera in order to measure the change in rotation angle from one frame to the next. Six new Slazenger hardcourt balls were used to fire six balls at intervals of about 2 sec onto each racquet before turning the camera off while mounting the next racquet.
A distance scale was mounted on the court and used to monitor distances, but the scale was also filmed when it was raised to the same height as the ball plane so that the distance travelled by the ball could be related to distances measured using the scale on the court. A calibration shot of the raised scale was taken whenever the camera was zoomed to a different distance, for example when changing the angle of incidence or when changing the ball speed.
Several of the racquets were impacted more than six times to improve the statistics and to gather data over a wider range of incoming ball parameters. The largest data sets were obtained using strings 3 and 7. For those strings, an additional six impacts was recorded at each of several different incident angles varying from 0 to 60 degrees. The same two strings, as well as string 15, were also chosen to measure the outgoing ball spin when the racquets were hand held in the same position and orientation as the clamped racquets.
III. BALL BOUNCE MODEL
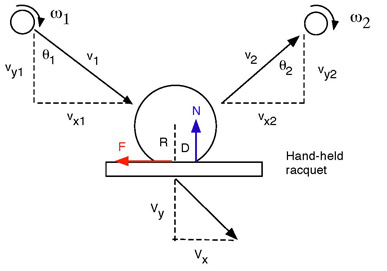
Fig. 2. Parameters used to describe the bounce of a tennis ball off a hand-held racquet. For most experiments, the ball was projected with backspin (i.e., with ω1 < 0).
The geometry of the bounce of a tennis ball off the strings of a hand-held racquet is shown in Fig. 2. A ball of mass m and radius R is incident obliquely at angle θ1 and speed v1 on a racquet that is initially at rest. The ball is shown as being incident with topspin, at angular velocity ω1. As a result of the collision, the racquet head will recoil, with velocity components Vx and Vy at the impact point, as indicated in Fig. 2, and the ball bounces at speed v2, at an angle θ2 and with spin ω2. It is assumed that the ball impacts in the middle of the strings and that the racquet does not rotate about its long axis. The same geometry can be used to model cases where the racquet is incident at finite speed, since the resulting ball speeds can be determined simply by changing the reference frame. In effect, the following calculations describe the result of such a collision in a reference frame where the racquet is initially at rest.
Two forces act on the ball, taken to be equal and opposite the forces acting on the racquet. We ignore the force of gravity and the force of the hand at the handle end of the racquet, since they are both much smaller than the impact force of the ball on the racquet, at least during the impact. A friction force, F, acts on the ball in the negative x direction, and a normal reaction force, N, acts on the ball in the positive y direction. The normal reaction force is assumed to act at a distance D ahead of the center of the ball. D is a quantity that can be estimated from experimental data when the bounce is filmed to determine the change in spin and velocity of the ball.

The time integral of the friction force is given by
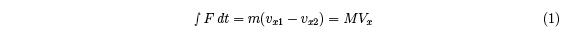
where M is the effective mass of the racquet at the impact point. M is typically about half
the actual racquet mass for an impact in the middle of the strings.3 The time integral of the
normal reaction force is given by
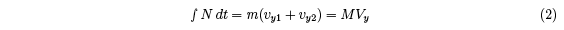
where vy1 and Vy are taken as positive numbers for convenience, even though the ball is
incident in the negative y direction, and the racquet recoils in the negative y direction. The
coefficient of restitution (COR) in the y direction is defined by
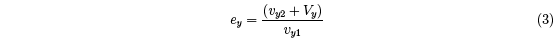
It is useful to define an apparent coefficient of restitution, eA = vy2/vy1, ignoring recoil of
the racquet. eA is related to ey by
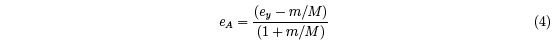
which is easily derived from Eq. (2). For a clamped racquet, where M is effectively infinite,
eA = ey ≈ 0.75 at incident ball speeds around 25 to 35 m/s. For a hand-held racquet, ey is
about 0.75 and eA is typically about 0.40, both for an impact in the middle of the strings.
In an analogous fashion, we can define a coefficient of restitution, ex, in the x direction,
by considering the tangential velocity of the contact point on the ball, given by vx – Rω. We
define ex in terms of the relative speed of the contact point and the racquet, by the ratio
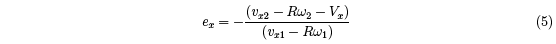
ex is a measure of the elastic energy stored and returned to the ball as a result of tangential
distortion of the ball and the strings. In the same way, ey is a measure of the elastic energy
stored and returned to the ball as a result of distortion of the ball and the strings in the y
direction.3-6
The ball changes spin during the bounce at a rate given by FR – ND = Icmdω/dt where
Icm = αmR2 is the moment of inertia of the ball about an axis through its center of mass.
For a tennis ball, α= 0.55.3 Hence,

Equation (6) provides a simplified expression for the change in angular velocity of the ball,
in that R, D and α are all assumed to remain constant during the bounce. In fact, the ball
squashes significantly during the bounce, in which case R will decrease to a value less than
that assumed in the following calculations, where we take R = 0.033 m. As a result, the term
FR overestimates the actual torque due to F and the true value of D will be over-estimated
by assuming that R remains constant. Since the time variation of R and Icm are unknown,
D can be regarded as a single parameter that combines the two non-ideal effects due to (a)
the change in ball radius and (b) the shift in the line of action of N during the bounce.
From Eqs. (1) to (6) we find that
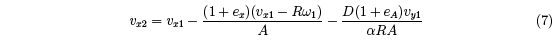
where A = 1 + m ⁄M + 1⁄α . We also find that
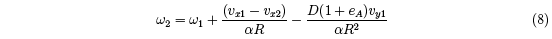
Since Vx is not easy to measure, it is useful to define a more easily measured quantity,
eT , that ignores recoil of the racquet and that represents an apparent tangential coefficient
of restitution.7 We define eT by the relation
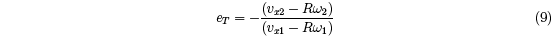
For a hand-held tennis racquet eT is typically about 0.01. For a clamped racquet, eT =
ex ≈ 0.1. Small variations in D and in ex (or eT ) are the primary causes of the differences
observed between different strings in the spin imparted to the ball. Those differences can
occur randomly from one bounce to the next on any given string, and can vary in a systematic
manner from one string to the next.
Alternative expressions for vx2 and ω2, based on the definition of eT , can be derived from
Eqs. (1)-(6), giving
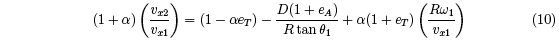
and
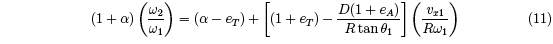
The rebound speed and spin depends not only on the elastic properties of the string and
the ball, as specified by the three parameters eT, D and eA, but also on the three parameters
v1, θ1 (or vx1 = v1 sinθ1 and vy1 = v1 cosθ1) and ω1 describing the incident ball. Equations
(10) and (11) appear to be cumbersome, but can be simplified. For example, if we take
α = 0.55 for a tennis ball, θ1 = 40°, and eA = 0.75 , eT = 0.1 as typical values for a clamped
racquet, then
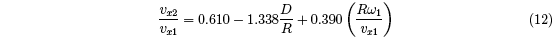
and
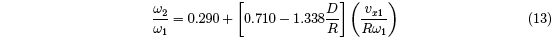
D/R was typically about 0.1 in our experiment and the main parameter affecting both the
spin and velocity ratios was the quantity Rω1/vx1. The outgoing spin of a ball therefore
depends mainly on the parameters of the incoming ball (i.e., its speed, spin and angle). The
dependence on string type and tension are smaller effects, and are not easy to measure.
Most of the rebound spin data was obtained with clamped racquets and with v1 = 23 ± 2 m/s, θ1 = 40° ± 2° and ω1 = –400 ± 30 rad/s. The primary objective was to compare spin generation by different strings, but the variation in the incoming ball parameters also affected the outgoing ball spin, and tended to mask differences between the strings. Two approaches were taken to minimize this problem. The first was to average the results of at least five bounces from each string, and to hand pick those bounces so that the average incoming ball parameters were approximately the same for each string. The second approach was to calculate eA, eT and D for each of the hand-picked bounces and then use Eq. (11) to calculate the outgoing ball spin for a standard set of incoming ball parameters.
The significance of small variations in each of the six parameters is summarized in Table 1 for the case of a clamped racquet. If v1 = 23 m/s, θ1 = 40°, ω1 = 400 rad/s, eA = 0.75, eT = 0.1 and D = 3 mm, then we find from Eqs. (10) and (11) that ω2 = +147.0 rad/s and vx2 = 2.05 m/s. The ball therefore bounces with topspin and with a large reduction in the tangential component of the ball speed (vx1 being 14.8 m/s). That is, the ball bounces almost at right angles to the string plane. If we increase the magnitude of each of the six parameters by 10%, one at a time, then the resulting changes in ω2 and vx2 are given in Table 1.
| Parameter | eA | eT | D | v1 | θ1 | ω1 |
|---|---|---|---|---|---|---|
| ω2 (rad/s) | 144.6 | 152.5 | 141.5 | 173.3 | 176.0 | 135.4 |
| % change | –0.6% | +3.7% | –3.7% | +17.9% | +19.7% | –7.9% |
| vx2 (m/s) | 1.98 | 1.95 | 1.87 | 2.77 | 2.89 | 1.54 |
| % change | –3.7% | –4.8% | –8.8% | +35.1% | +40.8% | –25.1% |
Table 1. Variations in ω2 and vx2 resulting from a 10% increase in one of the six parameters, as listed (ω1 was increased from –400 to –440 rad/s.)
It is clear from Table 1 that the outgoing spin and vx2 value (or rebound angle) are more sensitive to small changes in the parameters describing the incident ball than they are to small changes in string properties. For that reason, the parameters of the incoming and outgoing ball were carefully measured for each and every bounce, to determine eT, eA and D for each bounce, and then the outgoing spin was normalized using Eq. (11) to calculate the outgoing ball spin when v1 = 23 m/s, θ1 = 40° and ω1 = –400 rad/s. The reliability of such a procedure depends on whether eT, eA and D remain constant as the incoming ball parameters are varied. Evidence that they do, at least over a limited range of such parameters, is provided below.
IV. NORMALIZATION EXPERIMENTS
Raw, un-normalized data for string 7, showing ω2 vs θ1 for a clamped racquet, are presented in Fig. 3. The same data set was used to compile Fig. 4, where we have plotted the COR (ey), ex and D as functions of θ1 and ω1. The whole data set is plotted in (a), (b) and (c), while data obtained at θ1 = 41 ± 2 degrees are plotted in (d), (e) and (f). The COR for each bounce was calculated from Eq. (3) assuming that Vy = 0, ex was calculated from Eq. (5) assuming that Vx = 0 and D was calculated from Eqs. (1), (2) and (6).
As shown in Fig. 3, ω2 is a maximum when θ1 is about 50°. The decrease in ω2 at larger angles of incidence indicates that when θ1 > 50° the ball slides on the strings throughout the impact without gripping the strings.5,6
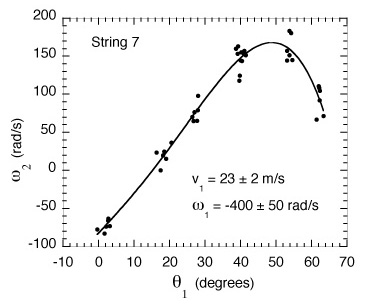
Fig. 3. Raw data for string 7 showing ω2 vs θ1 for a clamped racquet and for the range of incident ball parameters shown in the figure. The smooth curve is a best fit to the data points, each point representing a single bounce.
The movies below show the outgoing spin for balls incident at the angles indicated in Figure 3. Three observations are immediately obvious upon watching the movies: (1) the increase in spin as θ1 approaches 50 degrees, (2) the increase in ball travel on the strings as θ1 increases, and (3) how the incident -400 rad/s spin affects the rebound angle, θ2. (Note: it is easiest to see these effects if the movies are advanced frame by frame using either the left and right arrows on the keyboard or the movie progress bar.)
The manner in which the COR varied with angle of incidence was an unexpected result, although the increase in COR at high angles of incidence can be explained partly by the decrease in the normal component of the incident speed. When the normal component of the speed is reduced, distortion of the ball and the strings is reduced, leading to a smaller loss of energy in both the ball and the strings. Conversely, the normal component of the incident speed is a maximum when θ1 = 0, leading to maximum distortion of the ball and the strings and a significant reduction in the COR. The increase in COR at high angles of incidence might also be partly due to the depression formed in the string plane which would tend to deflect the ball in a direction closer to the normal. The depression will be largest at low angles of incidence, but the effect on the COR might be larger at high angles of incidence since the tangential speed of the ball is then larger.
The tangential COR, ex, is relatively constant at low angles of incidence, decreases to zero at about θ1 = 54° and is negative when θ1 > 54°. A negative value of ex implies that the ball remains in a sliding mode throughout the bounce. When ex is negative, the ratio ∫ F dt ⁄ ∫ N dt is then equal to the coefficient of sliding friction which was 0.56 ± 0.02 for string 7. For string 3, the coefficient of sliding friction was 0.64 ± 0.02.
The distance D increases with angle of incidence and is negative when the ball is incident at θ1 near zero (at least when the ball is incident with backspin, as it was). The latter result can be attributed to the fact that the front edge of the ball rotates out of the surface throughout the whole bounce, and the back edge rotates into the surface, when θ1 is positive and close to zero. As a result, the trailing edge of the ball enters the surface at a higher speed than the leading edge, so the normal reaction force is larger at the trailing edge. The same effect might be expected at all angles of incidence, but D is positive at high angles of incidence. In fact, the magnitude and sign of D appears to be related to the magnitude and sign of ω2, as can be seen by comparing Fig. 4(c) with Fig. 3. It is not obvious why this should be the case. Other effects could cause D to vary. For example, the ball moves forward in a depression formed in the string plane, so the front edge of the ball experiences a larger normal reaction force than the rear of the ball.
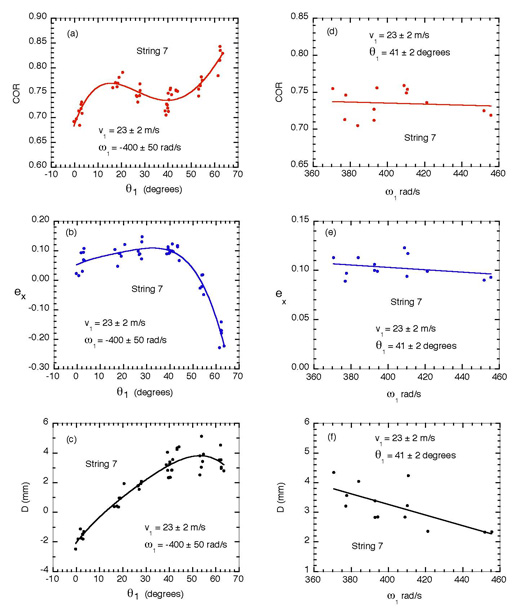
Fig. 4. Variation of COR, ex and D vs θ1 and vs ω1 for string 7, for the range of incident ball parameters shown in each figure. The angle of incidence, θ1 was varied deliberately over a wide range, while small changes in v1 and θ1 and larger changes in ω1 were caused by variations within the ball launcher. Each data point represents a single bounce. The smooth curves and lines are best fits to the data.
V. RESULTS WITH CLAMPED RACQUETS
The main significance of the results in Fig. 4, in terms of normalizing the data, is that the three string parameters ey, ex and D all remain approximately constant when v1 varies in the range 21 to 25 m/s, θ1 varies in the range 39 to 43 degrees and ω1 varies from –350 to about –430 rad/s. There are significant variations in the measured values of all three string parameters from one bounce to the next, but it is possible to measure all three parameters for any given bounce and then predict, from Eq. (11), the result that would have been obtained if v1 = 23 m/s, θ1 = 40° and ω1 = –400 rad/s for each bounce. Results for the clamped racquets are shown in Table 2, where the COR, ex and D entries are average values for each string, averaged over at least five bounces, and the ω2 entries are also averaged over the same bounces, having first normalized the measured ω2 data from each bounce in the manner described.
| String | Type | Tension | ERT | COR | ex | D (mm) | ω2 ±SD |
|---|---|---|---|---|---|---|---|
| Wilson NXT | N | 62 | 55 | 0.70 | 0.066 | 3.27 | 125 ± 11 |
| Wilson NXT | N | 52 | 46 | 0.73 | 0.041 | 3.53 | 106 ± 14 |
| Tecnifibre NRG2 | N | 62 | 53 | 0.76 | 0.056 | 2.72 | 128 ± 15 |
| Tecnifibre NRG2 | N | 52 | 46 | 0.72 | 0.063 | 2.88 | 130 ± 11 |
| Polyfibre TCS | P | 62 | 46 | 0.72 | 0.110 | 3.52 | 144 ± 8 |
| Polyfibre TCS | P | 52 | 40 | 0.71 | 0.102 | 3.63 | 138 ± 14 |
| Luxilon Alu Power | P | 62 | 55 | 0.73 | 0.102 | 3.15 | 146 ± 10 |
| Luxilon Alu Power | P | 52 | 46 | 0.78 | 0.097 | 2.05 | 162 ± 8 |
| Luxilon Original | P | 62 | 48 | 0.76 | 0.087 | 2.24 | 153 ± 12 |
| Luxilon Original | P | 52 | 46 | 0.75 | 0.098 | 2.63 | 153 ± 9 |
| Babolat Tonic Gut | G | 62 | 55 | 0.73 | 0.067 | 2.59 | 137 ± 7 |
| Babolat Tonic Gut | G | 52 | 46 | 0.78 | 0.089 | 2.52 | 149 ± 7 |
| Luxilon ALU Rough | P | 62 | 51 | 0.77 | 0.113 | 2.53 | 162 ± 8 |
| Luxilon ALU Rough | P | 52 | 40 | 0.76 | 0.121 | 2.62 | 165 ± 10 |
| RacquetFuel Control | P | 55 | 48 | 0.76 | 0.128 | 3.49 | 153 ± 13 |
| Old Nylon String | N | 58 | 42 | 0.75 | 0.065 | 3.30 | 122 ± 13 |
Table 2. Normalized data obtained for each of the 16 strings tested when the racquet head was clamped and the ball was assumed to be incident at v1 = 23 m/s, θ1 = 40° and ω1 = –400 rad/s. Tension and ERT values are in lb. Type N = nylon, P = polyester, G = natural gut. ω2 is the normalized rebound spin in rad/s.
There is no consistent variation in outgoing ball spin with string tension, but there is a clear difference with string type. The average spin for the four new nylon strings (1 to 4) was 122 rad/s, the same as the old nylon string (16). The average for the two gut strings (11 and 12) was 143 rad/s. The average spin for the nine polyester strings (5 to 15) was 153 rad/s, 25% larger than the four new nylon strings.
VI. RESULTS WITH HAND-HELD RACQUETS
Results obtained with strings 3, 7 and 15, when the racquets were hand-held, are shown in Tables 3 and 4. Table 3 gives a summary of the raw data for these strings, before normalization. Five bounces on string 3, eleven on string 7 and eight on string 15 were chosen as all having similar values of incident ball speed (22.6 ± 1 m/s), angle (40.7 ± 2° ) and spin ( –397 ± 26 rad/s), with average values for each string as shown in Table 3. Also shown in Table 3 is the average rebound spin for each string, and the standard deviation in ω2. The large standard deviation for string 3 was due to the fact that one particular bounce resulted in an abnormally low rebound spin, only 54 rad/s, since v1 and θ1 were both relatively low and ω1 was relatively large for that bounce. Nevertheless, there was nothing unusual about the values of eA, eT or D for that bounce and it was included in the data set and normalized together with four other bounces on that string. As a result, the standard deviation in the normalized spin for that string was significantly smaller, as indicated in Table 4.
| String | v1 | θ1 | ω1 | eA | eT | D (mm) | ω2 ±SD |
|---|---|---|---|---|---|---|---|
| Tecnifibre NRG2 | 22.6 | 39.3 | –392 | 0.39 | –0.006 | 3.28 | 90.5 ±22 |
| Luxilon ALU Power | 22.5 | 39.7 | –398 | 0.38 | –0.011 | 2.17 | 102 ±9 |
| RacquetFuel Control | 22.1 | 41.0 | –383 | 0.39 | –0.009 | 2.83 | 104 ±9 |
Table 3. Raw data results for hand-held racquets, averaged over five or more bounces.
Table 3 suggests that string 15 generates slightly more spin than string 7 and significantly more spin than String 3. However, the result for string 15 was obtained at a slightly larger average value of θ1 and a slightly smaller average value of ω1 than the other strings. When the results were normalized to the same incoming ball parameters for all three strings, as indicated in Table 4, then string 7 was found to generate more spin (on average) than string 15.
| String | v1 | θ1 | ω1 | eA | eT | D (mm) | ω2 ±SD |
|---|---|---|---|---|---|---|---|
| Tecnifibre NRG2 | 23 | 40 | –400 | 0.39 | –0.006 | 3.28 | 96 ±11 |
| Luxilon ALU Power | 23 | 40 | –400 | 0.38 | –0.011 | 2.17 | 110 ±9 |
| RacquetFuel Control | 23 | 40 | –400 | 0.39 | –0.009 | 2.83 | 101 ±7 |
Table 4. Normalized data for hand-held racquets
The results in Table 4 can be compared directly with those in Table 2 since the outgoing ball spin has been normalized to the same incoming ball parameters. The outgoing ball spin for the hand-held racquets decreased by 25% for strings 3 and 7, and by 34% for string 15, when compared with the corresponding clamped racquet results. This difference can be seen by comparing the following two movies of racquet 7 hand-held vs clamped.
The reduction in ball spin is not surprising, given that the normal force on the ball is reduced when the racquet is hand-held in a stationary position, resulting in a smaller rebound speed in the y direction, and a larger rebound angle. It is more surprising that, of the three hand-held racquets, string 15 generated the largest spin when the racquets were clamped, whereas string 7 generated more spin when the racquets were hand-held.
Of the three racquets, string 15 had the largest value of ex when the racquet was clamped, indicating greater energy storage and recovery due to motion of the string parallel to the string plane. However, it also had the largest value of D, an effect that tends to inhibit spin generation. It may be that string 15 performs best, in terms of spin generation, when the force on the string is relatively large. Experiments related to this possibility are described in the following section.
VII. MEASUREMENTS CONCERNING STRING MOTION
Figure 5 shows the tangential force acting on a string during a 40 ms impact. A 1 kg steel ball was attached to a single string in a fully strung racquet, by a length of flexible wire. The racquet was clamped to a frame with the strings in a vertical plane, and the steel ball was dropped vertically through a height of 10 cm to apply an impulsive force to the string. The magnitude of the force was about 100 N, similar in magnitude to the tangential force acting on the strings when impacted by a 23 m/s tennis ball in the previous experiments. An accelerometer mounted on the ball provided an output voltage proportional to the force on the ball and the string. The impact duration was longer than the usual 5 ms impact of a tennis ball on the strings. It is clear from the accelerometer signal that the string motion is "jerky," a result that implies that the string moves freely for a short distance, then gets stuck by static friction on overlapping strings and then slips again as a result of the increasing force. The behavior of the string for a 5 ms impact was not measured using this technique, but the result from the 40 ms impact suggests that the behavior of a string during a 5 ms impact could be quite erratic.
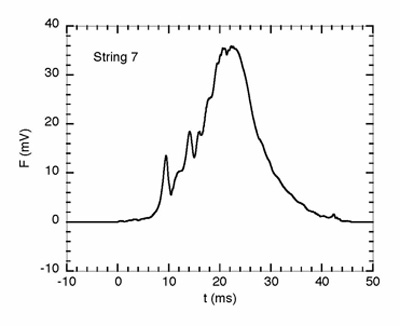
Fig. 5. Tangential force applied to a string, as measured by an accelerometer attached to a 1 kg steel ball.
The movie below shows the jerkiness of string motion in another way. The drop-down menu also has choices for the jerkiness of a nylon strings and the impact and string movement for most of the strings in our experiment. It is most revealing if you play the movies one frame at a time with the arrow keys on your keyboard or the movie's progress bar (Internet Explorer may not do this).
Motion of the strings in the tangential direction was filmed at 600 fps using a hand-held racquet when a ball impacted at an angle of incidence of 40°. Typical results are shown in Figs. 6 and 7. Some string types deflected more than others, but all strings were found to return to their original position as soon as the ball bounced off the strings. Strings near the leading edge of the ball deflected more than strings at the trailing edge when the ball was incident without spin, as shown in Fig. 6. When the ball was incident with backspin, at about –400 rad/s, strings near the trailing edge of the ball deflected more than strings near the leading edge, as shown in Fig. 7. These results provide qualitative support to our interpretation that elastic energy can be stored and returned within the string plane during the bounce and that the normal reaction force (and hence the friction force) is larger on one side of the ball than the other, depending on the direction of rotation of the ball.

Fig. 6. Impact on string 7 recorded at 600 fps for a ball incident without spin, at θ1 = 40°, v1 = 30 m/s. The racquet was hand-held and the ball was incident from right to left. The fourth vertical string from the left is displaced to the left at 3.3 ms and returns to its original position by 6.7 ms.

Fig. 7. Impact on string 7 recorded at 600 fps for a ball incident with backspin at ω1 = –400 rad/s, θ1 = 40° and v1 = 23 m/s. The racquet was hand held and the ball was incident from right to left. The ball bounced almost at right angles to the string plane, so there was very little right to left motion of the ball from 6.7 ms to 10 ms. The string displaced at the trailing edge of the ball returns to its original position by 6.7 ms.
VIII. BALL INCIDENT WITHOUT SPIN
Effects of changing the speed or spin of the incident ball were not studied in detail, but additional measurements were made with strings 3 and 7 when the incident spin was reduced to zero and when the incident speed was increased from 22 ± 1 m/s to 36 ± 0.4 m/s. For this set of measurements, the racquets were clamped and θ1 = 38.5° ± 0.6°. The results, normalized to an incident angle θ1 = 40°, are shown in Table 5. The main point of interest is that the outgoing spin increases when the incident spin is reduced to zero and it increases when the incident ball speed is increased. In each case, string 7 generates more spin than string 3. There is a reduction in the COR at the higher incident ball speed, and a significant increase in D. The increased spin for string 7 arises mainly because of its larger value of ex, given that the values of the COR and D are about the same for both strings.
| String | Type | v1 (m/s) | ω1 | COR | ex | D (mm) | ω2 ±SD |
|---|---|---|---|---|---|---|---|
| Tecnifibre NRG2 | N | 23 | –400 | 0.76 | 0.056 | 2.72 | 128 ± 15 |
| Tecnifibre NRG2 | N | 23 | 0 | 0.82 | –0.006 | 3.31 | 224 ± 4 |
| Tecnifibre NRG2 | N | 36 | 0 | 0.73 | 0.011 | 5.81 | 293 ± 12 |
| Luxilon ALU Power | P | 23 | –400 | 0.73 | 0.102 | 3.15 | 146 ± 10 |
| Luxilon ALU Power | P | 23 | 0 | 0.81 | 0.031 | 3.23 | 237 ± 6 |
| Luxilon ALU Power | P | 36 | 0 | 0.74 | 0.063 | 5.82 | 316 ± 7 |
Table 5. Normalized data obtained for strings 3 and 7 when the racquet head was clamped and the ball was incident at θ1 = 40° and ω1 = 0. For comparison, the result at ω1 = –400 rad/s is also shown. ω2 is the normalized rebound spin in rad/s.
Additional results were obtained for string 7 when the ball was incident with zero spin at right angles to the string plane (i.e., with θ1 = 0), both when the racquet was clamped and when it was hand-held. The main point of this experiment was to measure the change in speed and rebound angle of the outgoing ball as a function of the impact position on the strings. All previous results were obtained by allowing the ball to impact in the middle of the string plane, plus or minus about 30 mm in both the vertical and horizontal directions. If a ball is incident on a hand-held racquet and impacts at a point that does not coincide with the long axis of the racquet, then the racquet rotates about its long axis. It is well known that the outgoing ball speed is reduced if the racquet rotates in this manner, but the effect on the rebound angle of the ball has not previously been measured.
Suppose that the racquet rotates through an angle of 10° while the ball is in contact with the strings. The direction of the normal reaction force on the ball will also rotate by 10° during this time. It might therefore be expected that the ball will rebound at an angle of about 10° to the incident path. In fact, it was found that the ball rebounded back along the incident path within about 1° even when the racquet rotated by about 15°. This is shown by choosing the movie selection labeled "Perpendicular Off-axis hit" on the drop-down list below. Two additional off-axis impacts incident with -400 rad/s backspin are also shown for comparison. In some cases, the rebound angle was slightly greater than 1° , but the latter result was attributed to a slight misalignment of the racquet. In those particular cases, the ball was incident at an angle of about one or two degrees rather than at right angles to the string plane.
Results for the hand-held racquet are shown in Fig. 8, d being the horizontal distance of the impact point from the middle of the string plane, the racquet being mounted in the orientation shown in Fig. 1. For a hand-held racquet, the ACOR (eA) is defined by Eq. (4).
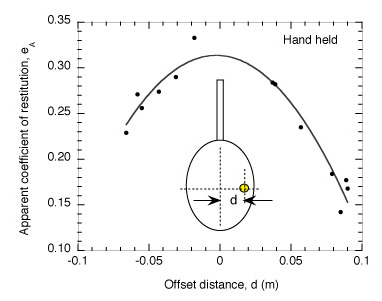
Fig. 8. Measurements of eA vs d for balls incident normally at 29.6±0.6 m/s on a hand-held racquet. Each data point corresponds to a single bounce.
IX. DISCUSSION AND CONCLUSION
The results obtained in this paper support those previously obtained by the ITF, and commonly reported by players themselves, indicating that polyester strings generate more spin than nylon strings. Most of our data were obtained using clamped racquets where we found that the outgoing spin from a selected group of polyester strings was 25% greater, on average, than a sample of four nylon strings, at least under the test conditions. Some strings generated more spin when strung at high tension, while other strings generated more spin when strung at low tension.
Results obtained with clamped racquets do not necessarily correlate well with those obtained with hand-held racquets. Insufficient data was obtained to draw firm conclusions, but the hand-held results obtained with three strings indicate that the resulting spin is about 30% smaller off a hand-held racquet than off a clamped racquet, for the same incoming ball parameters.
The mechanisms involved in spin generation were not clearly identified but appear to be associated with string movement within the string plane. Evidence was found that string movement tends to be erratic, resulting in variations in the outgoing spin from one bounce to the next.
It was found that the outgoing spin depends more sensitively on the incoming ball parameters than on string parameters themselves. For that reason, considerable care needs to be taken when comparing different strings to ensure that the incoming ball parameters are either carefully controlled or carefully measured in order to normalize the outgoing ball spin to the same incoming ball parameters.
It was found that the rebound angle off the strings, for a hand-held racquet, is not significantly affected by rotation of the racquet during the impact. The outgoing ball speed is reduced if the racquet rotates, but the rebound angle is not affected since the rotation angle of the racquet remains very small while the ball compresses, even at incident speeds as high as 30 m/s and even when the ball impacts near the outer edge of the frame.
References
1 S. Goodwill, J. Douglas, S. Miller and S. Haake, "Measuring ball spin off a tennis racket," In
Proc. of the 6th Int. Conf. on the Engineering of Sport (ed. F. Moritz and S.J.Haake), Springer,
New York (2006). Vol. 1, 379-384.
2 S. Miller, "The role of ITF Science & Technical in evaluating and regulating tennis equipment,"
In Proc. of the 3rd Int. Conf. on Tennis Science & Technology (ed. S. Miller & J. Capel-Davies),
1-19 ( 2007).
3 H. Brody, R. Cross and C. Lindsey, The Physics and Technology of Tennis, Racquet Tech
Publishing, Solana Beach (2002), 348-357.
4 R. Cross, "Measurements of the horizontal coefficient of restitution for a superball and a tennis
ball," Am. J. Phys. 70, 482-489 (2002).
5 R. Cross, "Grip-slip behaviour of a bouncing ball," Am. J. Phys. 70, 1093-1102 (2002).
6 R. Cross, "Bounce of a spinning ball near normal incidence," Am. J. Phys. 73, 914-920 (2005).
7 R. Cross and A. Nathan, "Experimental study of the gear effect in ball collisions," Am. J. Phys.
75, 658-664 (2007).
8 Goodwill, S.R. and Haake, S.J., (2004) Effect of string tension on the impact between a tennis
ball and racket, The Engineering of Sport, Research, Development and Innovation: Proceedings
of the 5th International Conference on the Engineering of Sport (ed M. Hubbard, R.D. Mehta
and J.M. Pallis), International Sports Engineering Association, 2, 3-9


