Abstract

According to intuition, belief, assumption, and marketing, there is a connection between paddle thickness, stiffness, and core material that manifests in power (shot speed). Beliefs run the gamut saying any one of these properties either increases or decreases power. But whatever is believed, it is usually quite adamant, in spite of other's equally staunch defense of the opposite. Likewise, manufacturers make seemingly contradictory claims about their paddle compared to others. Without measurement, making sense of all this is difficult. This experiment puts all these assumptions to the test.

1. Introduction

Pickleball paddles are generally composed of a honeycomb polymer interior sandwiched between two graphite or fiberglass surfaces. However, there are also some paddles that are constructed solely of graphite fiber layups with a graphite surface adhered to both sides. Much is claimed and believed about the contributions of thickness, surface compressibility, and stiffness to the enhancement of power, control, and comfort of the paddle.

These beliefs are curious given the rules restraining compressibility which leave very little room for variances in core or face construction to significantly alter measured performance results. USA Pickleball has two rules that relate to the material type and compressibility[1]:

• 2.E.6 Prohibited Surface Features and Mechanical Features.
• 2.E.1 Material. The paddle must be made of any material deemed safe and not prohibited by these rules. The paddle shall be made of rigid, non-compressible material meeting the criteria located on the USA Pickleball and IFP websites.
• 2.E.6.f Springs or spring-like material, flexible membranes or any compressible material that creates a trampoline effect.

The effect of the second rule regarding the trampoline effect of the surface material was examined in another experiment (Pickleball Spin: Why Is A Rubber Hitting Surface Illegal?)

USAP tests the compressibility regulation by applying a static load to the center of a paddle supported at its periphery. Based on the measuring procedures, the allowed deflection is ≤ 0.005 inches (0.127 mm).

In contrast, this experiment uses a dynamic procedure to test both compressibility and bending. Deformation acts like a rubber band — it stores a portion of the deformation energy as elastic energy to be returned to the impacting object. This experiment measures and tracks the flow of this deformation energy to determine its contribution to rebound velocity ("power"). The experiment will determine the impact properties of the paddle alone, ball alone, and paddle and ball together. These properties are measured and calculated in a clamped, stationary condition. These properties are then used to calculate the rebound "power potential" of balls rebounding from paddles during free, unsecured impacts.

2. Experiment

Eighty-two paddles were tested using the experimental setup shown in Figure 1. The paddle is secured at the tip, throat, and butt, and a 1.18 kg mass is dropped from 20 cm above the paddle to impact 30 cm from the butt end of the paddle.

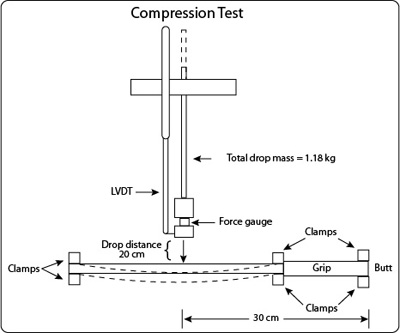
Figure 1 — Test device to measure paddle bending, compression, stiffness, impact duration, and rebound speed. Test is preformed near the middle of the paddle, 30 cm from the butt.

2.1. COR measures velocity return

The coefficient of restitution (COR, or e) is the ratio of the relative rebound speed to the relative incident speed of the two colliding objects. COR is given as

(1)      e = -(V_y2 - v_y2) / (V_y1 - v_y1)

where V_y1 and v_y1 are the incident speeds of the paddle and ball respectively, and V_y2 and v_y2 are their rebound speeds, the subscript y indicates perpendicular to the surface, subscripts 1 and 2 indicate incident and rebound, and the leading minus sign corrects for change in direction of the ball. COR gives an indication of how much energy was lost or returned by the two objects during the collision. But it is difficult to determine how much energy was lost/returned by each separately in order to determine the energy property of each object. The experiment secures the paddle such that the only change in velocity is that of the impact mass — the paddle velocity is zero before and after the collision. The COR ratio then simplifies to the rebound speed divided by the incident speed of the impact mass — e = -v_y2 / v_y1. COR has values between 0 and 1.0.

COR is the ratio of velocities and as such it is referred to as the "power potential" in sports terminology. COR squared is equal to energy return. If COR = 0.6, then energy return is (0.6)² = 0.36, or 36%. If COR is 0.6, then the perpendicular rebound speed will be 0.6 of the perpendicular incident speed.

2.2. Test requirement: direct all impact energy into the paddle

Two procedures are necessary to properly determine COR. First the paddle must be clamped and stationary to prevent any energy being converted into linear or rotational motion and thus not available to give back to the impact device (or ball). Second, the solid impact head of the drop mass must be much stiffer than the paddle. This is because the total energy of the collision will be divided inversely to the respective stiffnesses of the colliding objects. Most of the energy will go into the softer object (the ball in play or the paddle in the test apparatus). Each object will then return a portion of its energy share in proportion to its restorative abilities, as indicated by its COR. Because the impact mass head is much stiffer than the paddle, virtually all the energy is directed into the paddle and the resulting energy return is a consequence of the paddle alone.

2.3. Stiffness determines the flow of impact energy

The resistance to deformation is measured as stiffness, k. Deformation in this experiment is the combination of local surface compression and transverse bending of the paddle head between the tip and throat clamps. The latter accounts for over 99% of the total deformation. Stiffness is given as

(2)      k = F / x

where F is the average force during impact and x is the transverse displacement of the impact point and k the stiffness. Stiffness is typically measured in N/m, N/mm, or lb/in. As such, stiffness is a measure of how much force (newtons or pounds) is needed to deform the paddle 1 meter or 1 mm or 1 inch.

Stiffness will become an important tool below when we extrapolate from the clamped paddle condition to actual ball-paddle collisions on court, in which case we will need to know the individual stiffness and COR properties of the paddle and ball.

3. Results

In a clamped paddle condition, COR primarily depends on materials and structure because there is no recoil motion of the paddle to siphon away energy. Recoil speed and energy depend on the quantity and distribution of mass. We have controlled for both by clamping the paddle so it cannot move. Initially, we want only to see what effect material, thickness, and stiffness have on energy return. In other words, is the face of the paddle and the interior core construction important to power and how important? Are there other properties that are more important to final ball velocity than paddle face and core construction?

3.1. Clamped paddle results

The graphs in Figures 2 and 3 show a weak negative correlation between COR and thickness and no relationship of COR to stiffness. Not only is there little or no correlation of stiffness or thickness to COR, but there is little difference between the CORs of different paddles. This is contrary to reports from players who believe that thickness, stiffness, and power are all connected and produce large differences between paddles.

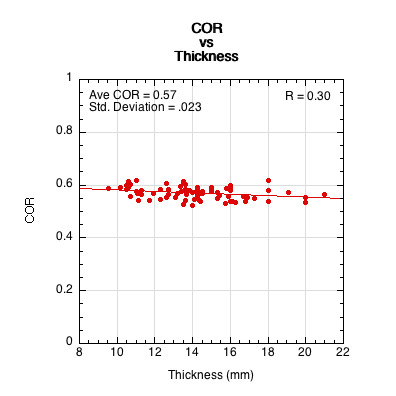
Figure 2 — There is a weak negative correlation between paddle thickness and COR for impacts near the center of a clamped paddle.

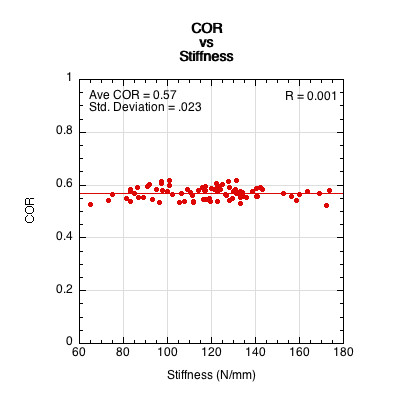
Figure 3 — There is no correlation between stiffness and COR for impacts near the center of a clamped paddle.

3.2. Ball COR Results

Next we need to know the COR and energy return of the ball alone in a clamped, stationary condition. Ball COR is actually given in the pickleball equipment rules, and we have also done ball COR and stiffness tests similar to the paddle tests described here. The rules state that a ball dropped from 78 inches onto a granite plate must bounce between 30 and 34 inches. Bounce height divided by drop height equals energy return. So, 30 / 78 = 0.385 and 34 / 78 = 0.436. COR is the square root of energy return, so COR must therefore be between √0.385 = 0.62 and √0.436 = 0.66. The COR in our experiments was 0.66, and the ball stiffness was 39 N/mm (222 lb/in). We will use those numbers in our calculations below.

3.3. Flow of Energy Between Paddle and Ball

Having determined the COR, energy return, and stiffness of the paddle and ball in the stationary, clamped condition, we can now trace the flow of energy between the clamped paddle and ball.

Energy flow begins with the total impact energy being divided between the paddle and ball in inverse proportion to their stiffnesses. Energy share of the paddle (ES_p) is equal to ball stiffness divided by the sum of paddle and ball stiffness (ES_p = k_b /(k_p + k_b ), and the ball energy share (ES_b) is equal to paddle stiffness divided by the sum of paddle and ball stiffness (ES_b = k_p /(k_p + k_b )). The energy shares of the 82 paddles are displayed in Figure 4.

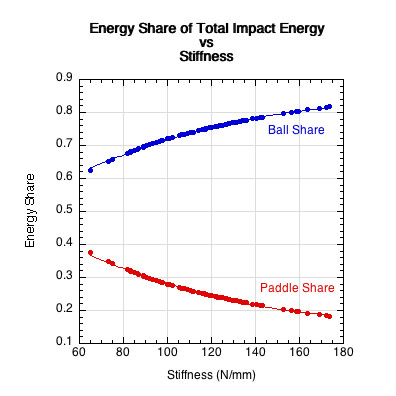
Figure 4 — Because the paddle is typically 1.2-3.2 times as stiff as the ball, up to 3 times as much energy is stored in the ball compared to the paddle.

The energy is now divided between the ball and paddle. The energy return ratio of each is equal to COR² (or e²). This is shown in Figure 5.

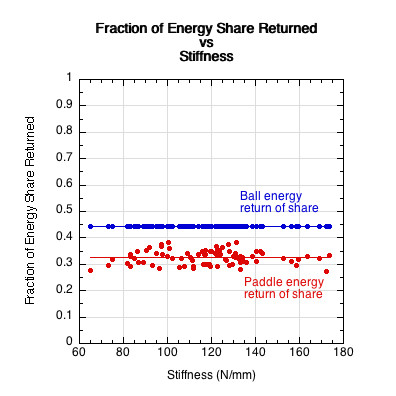
Figure 5 — The fraction of the stored energy that will be returned. Not only does the ball store more energy than the paddle, it also returns a larger fraction of that share than the paddle.

Figure 5 shows that the energy return of the ball is given as constant because the energy return of every ball must be similar by the rules (38.5-43.6%). In this experiment, the energy return was 43.5% (Selkirk Competition outdoor ball). Likewise, we could have used the average COR of all paddles to generalize the results but left the scatter to demonstrate the potential variability, minimal as it may be.

The energy returned by the paddle and the ball equals the energy return ratio (Fig. 5) times the energy share (Fig. 4). The result is shown in Figure 6.

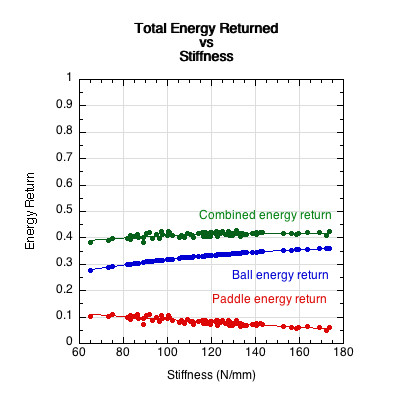
Figure 6 — The percent energy returned (Fig. 5) times the percent energy stored (Fig. 4) equals the total energy returned by the paddles and ball (Fig. 6). The sum of these energies is the total energy directed into the rebounding ball.

As paddles get stiffer they store less energy and return less. Consequently, the ball stores more and returns more, but not a great deal more. The minimum combined energy return is 37% (COR = .608) and the maximum 42% )(COR = .650). Interestingly, whereas Figure 4 showed no correlation between COR and stiffness when all the energy went into the paddle alone, COR is dependent on stiffness when the paddle shares impact energy with another softer object (combined energy return correlation: R = 0.52). In this way we see that material properties alone account for about 5% difference in rebound performance of a clamped, unmovable paddle when impacted with another less stiff object (ball). However, as we will see below, this seeming importance of paddle stiffness can be virtually neutralized depending on the amount and distribution of mass.

The results shown in Figures 4-6 are of a ball bouncing from a clamped paddle. These results describe the structural properties of the paddle — the material and architecture. These properties can now be used to predict the behavior of free, unclamped ball-paddle impacts. When the paddle is not secured and stationary, some of its energy share will be converted into motion, not elastic energy, and thus will not be available to be given back to the ball. So, in an unclamped condition, the paddle will still return energy according to its COR (fig. 5), but it will have less energy to work with. How much less depends on the amount and distribution of the mass as manifest at the impact location. This is known as the effective mass.

3.4. Effective Mass

The greater the mass the more difficult it is to lift. This resistance to motion is measured as weight. A rod with a mass on the opposite end from your hand is more difficult to swing in a circle than one without mass. This resistance to rotation about an axis is measured as moment of inertia (in racquet sports terminology, "swingweight" or "twistweight", depending on the axis). At any given impact location on the paddle, weight, swingweight, and twistweight combine into the effective mass of that impact location. This is known as the "hittingweight". It is calculated "as if" the ball impacted with a discrete point with a mass equal to the hittingweight. The hittingweight is always less than the actual weight, unless the impact is at the center of mass (balance point) of the paddle. Larger hittingweights result in less energy loss due to motion than than do smaller hittingweights. The hittingweight for a ball impacting along the center axis from tip to butt is given as

(3)      M_e = MI_cm / (I_cm + Mb²)

where M is the mass of the paddle, I_cm is the swingweight around an axis through the center of mass, and b is the distance from the impact point to the balance point.

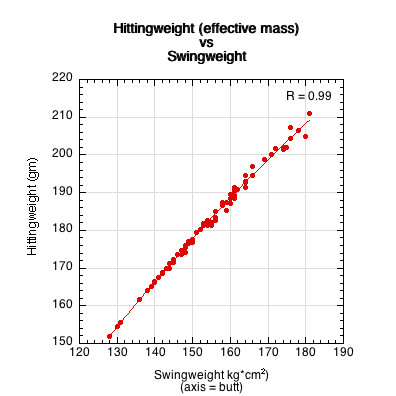
Figure 7 — Hittingweight is the effective mass of the hitting location. It is a function of swingweight, which is more commonly reported and measured. Swingweight is thus commonly used as an qualitative equivalent parameter for hittingweight.

3.5. Apparent Coefficient of Restitution (ACOR)

The associated property to COR is ACOR (apparent coefficient of restitution, e_A, or "power potential"), and it is given as

(4)      e_A = -v_y2 / v_y1

where e_A is ACOR, and v_y2 and v_y1 are the speed of the ball perpendicular to the paddle after and before contact. COR measures the relative speed of the ball to the paddle before and after contact. ACOR only measures the speed of the ball to the lab or court, ignoring the change in speed of the paddle due to the impact. In a clamped paddle situation, the paddle does not move and e_A = e. When the paddle is stationary but free to move, e_A simply ignores the change in paddle speed since it is difficult to measure and all we care about is the resulting speed of the ball anyway. ACOR is less than COR because it only accounts for the speed of one of the two objects in the collision. ACOR will be the same whether a ball impacts a stationary paddle, a paddle impacts a stationary ball, or the paddle and ball impact each other. When both the paddle and ball are unconstrained and free to move (recoil, rotate, and twist), then the resulting change in speed of each depends on their relative masses and the distribution of mass in the paddle — the hittingweight. ACOR can be derived if COR and hittingweight are both known by the formula

(5)      e_A = (eM_e - m) / (M_e + m)

where M_e is the hittingweight, m the mass of the ball, e is COR, and e_A is ACOR. Figure 8 shows the result of this calculation.

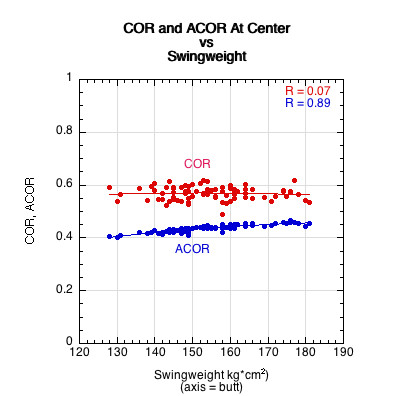
Figure 8 — ACOR is less than COR. COR is fairly constant at all swingweights, but ACOR increases with swingweight. Swingweight (and hittingweight) is the only parameter that is commonly measured which significantly correlates to performance — specifically to power, but also anecdotally to comfort and feel.

Figure 9 is a zoomed in view of the dependance of ACOR on swingweight.

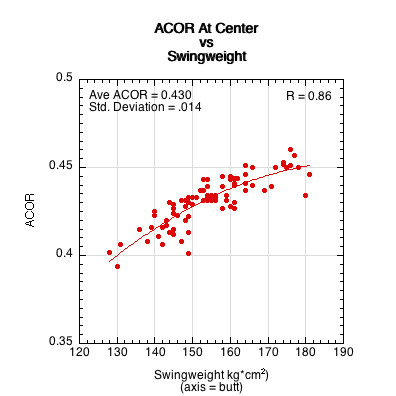
Figure 9 — A zoomed in view of the dependance of ACOR on swingweight (and hittingweight).

We see that the rebound speed depends on mass distribution as manifested in swingweight and hittingweight. These are kinematic properties of the paddle as opposed to structural material properties. How, then, is material stiffness correlated to a ball bouncing from a free standing paddle? Figure 10 shows that compared to mass distribution, the material property itself has little correlated influence on rebound.

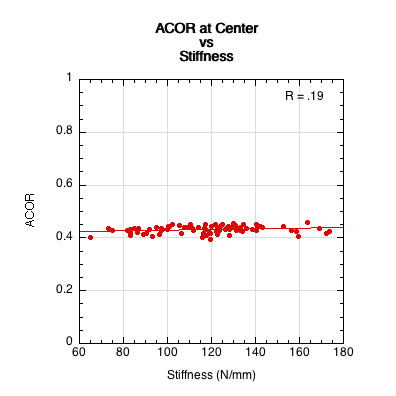
Figure 10 — Paddle stiffness has only a weak correlation with final rebound performance of ball on a paddle. Any such influence is minimized by the influence of the quantity and distribution of mass.

Figure 10 shows that the final effect of paddle stiffness on ball velocity is somewhat neutralized by the influence of quantity and distribution of mass. It would seem that at the end of the day, you can say whatever you wish about the materials and structure of a paddle, but what really matters to power is quantity and distribution of mass.

4. Discussion and Analysis

ACOR tells us everything we want to know about a paddle — the net result of a paddle's weight, swingweight, twistweight, hittingweight, balance, material, size, shape, length, thickness, stiffness, etc. But does one of these constituents tell us almost as much as ACOR while being much easier to measure? Swingweight does just that. The distribution of mass is measured as moment of inertia, or in sports terminology, swingweight and twistweight. Swingweight is the resistance to rotation about an axis perpendicular to the paddle face, typically measured at 10 cm from the end of the handle on commercial devices. It is also measured at the end of the handle (in this experiment), or at the center of mass. Twistweight is resistance to rotation about the lengthwise tip-to-butt axis. Measuring swingweight at the butt end makes the most sense because that is closest to the actual axis of rotation (at the wrist or higher up the arm when calculated as center of curvature as the sum of paddle and arm rotations). Resistance to movement is calculated as the sum of every atom of mass in the paddle times the square of that atom's distance to the rotation axis. The larger that sum, the harder it is to rotate the paddle around the given axis.

The results of this experiment indicate that the energy return property of all paddles is approximately the same when considered as non-moveable structures. The material, stiffness, and architecture of every paddle returns about the same velocity and energy when all of the impact energy is directed into paddle deformation, storage, and return. However, when the impact energy is allowed to be split up and shared between the two colliding objects, then differences appear. In that case, the energy is divided between the objects in inverse proportion to their stiffness. Then, a fraction of that energy share is returned based on the energy return ratios determined in the clamped paddle tests. But the energy share fraction that is available to be returned is reduced by the energy used in moving the paddle. The movement is minimized as hittingweight increases.

In all cases tested, the ball stores more energy and gives back more than the paddle. When the paddle stiffness declines, the paddle gets a larger energy share and the ball less. But since the paddle's energy return ratio is less than the ball's, this actually reduces the energy return — more energy is stored in the less efficient paddle and less in the more efficient ball.

5. Conclusion

Static tests to determine properties can be misleading because they measure a property of a paddle in isolation of how that property behaves in dynamic interactions with a ball. Measuring the isolated property is necessary to determining the dynamic interactional outcome between ball and paddle, but extrapolating that result without performing a dynamic interactional analysis can result in incorrect conclusions. This was demonstrated by how the interpretation of the role of stiffness changed depending on the context of the test.

Given the average construction of paddles and balls, and further given the restrictions the equipment rules place on paddle properties, it appears that the only way to significantly alter the rebound performance of a paddle is by altering the amount and distribution of mass. That doesn't seem to leave much room for new paddle development and technology. We are not aware of any studies that examine the effect of building paddles that specifically incorporate properties that violate the equipment rules — except the TWU study on applying a rubber surface to the paddle to effect spin and power: Pickleball Spin: Why Is A Rubber Hitting Surface Illegal? It would be interesting to test some such paddles. The rules exist to protect the nature of the game and to prevent unfair advantage due to equipment. But what changes to equipment do indeed so affect the game and give unfair advantage? And what changes could improve the game? Further study is needed.

6. References

[1] USA Pickleball, "2021 Equipment Standards Manual", https://usapickleball.org/docs/eec/Equipment-Standards-Manual.pdf.
[2] C. Lindsey, "Pickleball Spin: The Role of Surface Roughness in Spin Generation", href="https://twu.tennis-warehouse.com/learning_center/pickleball/pickleballspin.php".