Abstract

The pickleball equipment rules forbid any surface features that allow a player to impart "excessive" spin to the ball. A rubber surface is explicitly referenced as one such feature. Rebound spin is determined by many factors: coefficient of friction, normal force offset, friction reversal, and horizontal elastic recovery. The first three factors are primarily friction-only events, and it has been shown that all paddles produce the same spin for most commonly hit shots, no matter how the friction is altered [1]. However, spin-inducing torque resulting from horizontal elastic energy return is an entirely different matter. An experiment was preformed to investigate the difference between a friction-only surface and a friction-plus-elastic surface. A table tennis rubber was secured with double-sided tape to the hitting face of a pickleball paddle. Balls were fired at incident angles from 10-90 degrees to the surface and the rebound spin and speeds were recorded. The rubber-surface paddle produced twice the spin of the non-rubber paddle and about 14% more velocity. This substantial difference was compared to the minimal differences in spin generated by "friction-only" surfaces. A discussion of revisiting the friction rules for paddles is included.

(Note: Click here to go staight to the results.)

1. Introduction

Torque causes spin. Torque is an off-center force that produces rotation around some axis. In pickleball, that axis will be the center of the ball. There are several torques that contribute to spin. We will discuss three below — friction, normal force offset, elastic recovery. Figure 1 will be helpful in visualizing the torques, spins, and bounce from the paddle.

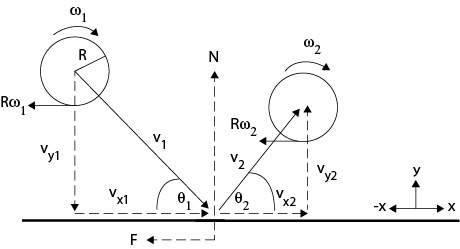
Figure 1 — Bounce geomentry. ω₁ and ω₂ are angular velocity before and after impact. v₁ and v₂ are velocity before and after. θ₁ and θ₂ are incident and rebound angle, v_x1 and v_x2 are the horizontal velocity components, and v_y1 and v_y2 the perpendicular velocity components. F is the friction force and N the normal (perpendicular) force.

1.1. Torque Due To Friction

The friction force opposes the motion of objects sliding against each other. In pickleball it operates at the contact surface between the ball and paddle and in the opposite direction of the ball's motion. Friction acts to slow and spin the ball. Most pickleball players believe that a rougher paddle surface produces more spin than a smooth one because it will more securely grip the ball and thus be better able to apply the force. As we will see below, this belief has limited practical application and is misconceived on two accounts.

1.1.1 Roughness Is Relative

The first misconception is in thinking that the look, feel, or measurement of roughness of one paddle compared to another is a good indicator of spin potential. What is important is the mutual roughness of the intersection between paddle and ball and how those surfaces fit together topographically on a microscopic level. "Rough" to the touch or to sight does not necessarily mean "rough" to the ball or paddle when in contact with each other. The degree of inter-locking between surfaces determines how they will move across each other, whether that be sliding, rolling, or gripping.

1.1.2. The Spin Limit

The second error in the "rougher = spinnier" maxim is that there is a maximum friction-induced spin limit. The spin limit occurs when friction decreases the sliding speed and increases the spin speed until they are equal but opposite direction at the contact point (Section 1.1.4). The spin limit increases at more oblique impact angles to the surface because more incident ball speed is parallel to the surface (sliding speed). However, it does not matter how rough or smooth the surface interface is — at any given impact angle, if the incident speed and spin are the same for any two paddles, then the maximum spin from friction is the same. Figure 2 demonstrates this by comparing the rebound spin from two paddles with average incident speed of 6.7 m/s with backspin. The smooth green curve is the spin limit curve (calculation explained in Pickleball Spin: The Role of Surface Roughness in Spin Generation).

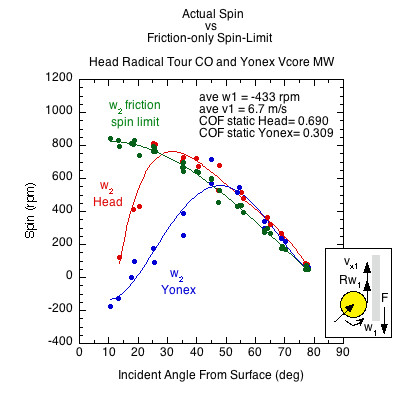
Figure 2 — Spin Limit Example. The rebound spins of two paddles (Head Radical Tour CO and Yonex Vcore MW) are compared against each other and the spin limit. The paddles have a substantial difference in static coefficient of friction but produce the same spin (equal to the spin limit) at all impact angles above 45 degrees. At more oblique angles below 45 degrees, the higher COF paddle produces more spin, but few pickleball shots are hit at those angles. In the "all-the-same" spin region above 45 degrees, there are small variances between the produced spin and the theoretical spin limit. These variances are explained below in the sections on normal force offset and friction reversal.

Figure 2 shows that in spite of the substantial difference in roughness (as measured by static coefficient of friction and discussed below), both paddles achieve the spin limit at all impact angles above about 45 degrees. The Head paddle achieves the spin limit at all angles above about 20 degrees. In general, at incident angles greater than 60 degrees from the surface, virtually all paddles reach the spin limit, regardless of roughness, and the majority of paddles achieve the spin limit at all angles above 45 or 50 degrees from the surface. Below 60 degrees, rougher paddle-ball interfaces achieve the limit at lesser and lesser angles than do smoother ones. But that seeming advantage is virtually irrelevant because the incident angle of most pickleball shots is greater than 45 degrees, meaning that most all paddles hit the same spin most of the time.

Every paddle has an angle below which it cannot achieve the spin limit (Yonex 45 degrees and Head 20 degrees in Figure 2). At those lower impact angles, the paddle will produce less spin than paddles that achieve maximum spin. This transition angle is also the angle at which the paddle will achieve its maximum possible friction-caused spin.

The spin limit depends on the coefficient of friction and contact velocity.

1.1.3. Coefficient of Friction

The inter-surface resistance to motion is quantified by the coefficient of friction (COF or μ). This is a ratio that asks: Compared to the force pushing the two surfaces together, how much force is necessary to move one surface against the other? The COF is given as

(1)      F / N = μ

where F is friction, μ the coefficient of friction, and N the normal (perpendicular) force pushing the objects together.

If the COF is 0.5, that means that it takes half as much force to initiate movement of the couch across the floor as it does to lift it (weight is the force pushing the couch against the floor). A low COF is good news to a furniture mover, but a pickleball player wants a high COF to enable hitting maximum spin on more oblique impacts.

There are actually two kinds of friction coefficients of concern — static COF (μ_s) and sliding COF (μ_k), where subscripts s and k stand for "static" and "kinetic". For a given normal force, the static coefficient is larger than the sliding coefficient because more force is required to start an object sliding across a surface than to continue its motion once it has begun.

1.1.4. Contact Velocity

The friction spin limit occurs for a simple reason: the contact point of the ball stops sliding when the linear velocity of the ball along the surface is equal and opposite to the spin speed at the surface. The contact velocity (v_c) during impact is given as

(2)      v_c = Rω - v_x

where v_x is the sliding velocity parallel the paddle, R is the ball's radius, ω is the angular velocity, and Rω is the "spin speed" (e.g., meters per second). For the usual case of incident linear (v_x) and spin speeds (Rω) being in the same direction at the contact point, the friction force (F) will act to reduce v_x and reverse and increase Rω. This process will continue until v_x = Rω (i.e., until linear speed is equal and opposite to spin speed). At that point the ball grips the paddle and sliding friction is terminated. If there is no relative motion of the surfaces (no sliding), there is no sliding friction acting to change the spin or speed of the contact point.

There are other impact scenarios besides the "usual case" of incident linear and spin speeds in the same direction as described above. v_x and Rω may also be incident in opposite directions and v_x may be greater or less than Rω. These permutations effect the direction friction acts, but the end result is the same — linear and spin speeds are changed until they are equal and opposite each other, whereupon any significant change in spin ceases.

1.1.5. Friction Reversal

After the ball grips the paddle, the contact region of the ball becomes "stuck." Static friction now takes over from sliding friction. Static friction acts to resist reinitiation of sliding. However, although the contact region is stuck, the rest of the ball continues to move forward and rotate. This causes a forward and downward deformation of that part of the ball. This deformation tries to pull the ball forward. Also, as the upper ball tries to rotate, it gets stopped at the stuck contact point. This causes a compressive pushing in front of the stuck point and a stretching pull behind the stuck point. The combination of the static friction and rotational pressures results in grip release, whereupon the contact region begins sliding backward. This initially increases spin. But, at the same time, the backward sliding contact region now also causes a forward directed friction force to resist the sliding. This friction reversal reduces the spin already achieved. Depending on the ball and sport, this reversal process can take place several times during impact, but it will typically occur only once for a pickle ball. The timing of the torques exerted by static friction and friction reversal contributes to the small variances in actual spin from the theoretical spin limit. These variances are referred to as "overspin" or "underspin" depending on the circumstance. The variance is quantified by the "spin ratio" which is given as

(3)      S₂ = Rω₂ / v_x2

where S₂ is the ratio at the end of impact. If S₂ = 1, then the spin limit condition of Rω=v_x is met. If S₂ > 1, then the ball bounces with overspin, and if it is less than 1, it bounces with underspin.

1.2. Torque Due To Normal Force Offset

Another spin-inducing torque is due to the normal force offset. If two objects are very stiff, there is very little deformation and the normal force pushing the objects apart is directed close to or through the center of mass (CM). If the ball is relatively soft compared to the paddle, it will deform both vertically and horizontally. Horizontal deformation is caused by the top of the ball continuing forward as friction is slowing the bottom of the ball. It is also caused by spin rotating into the front or back of the ball's travel. This shifts the normal force forward or backward of the CM, thus creating a torque that decreases or increases spin, depending on its direction compared to the friction force.

1.3. Torque Due To Elastic Force

A portion of the energy it takes to deform the ball or paddle is stored and returned to the ball. If the paddle has an elastic, high energy return surface, it can add speed and spin to the rebound. In that case, both the friction and elastic force will act opposite the direction of the contact point to slow the ball, increase the rebound angle from vertical, and increase spin. Since rubber surfaces are outlawed in pickleball, only friction comes into play to increase spin, and as we have seen, friction has a maximum spin limit. If there is horizontal, elastic snap-back, the friction spin limit can be greatly exceeded.

Energy return can be measured both vertically and horizontally. Energy return perpendicular to a clamped, secured paddle is measured by the coefficient of restitution (e_y). This is the ratio of the perpendicular rebound speed to the perpendicular incident speed

(4)      e_y = v_y2 / v_y1

and has values between 0 and 1.0.

The horizontal energy return from a clamped paddle is measured by the tangential coefficient of restitution (e_x). This is given as the ratio of the contact speed just after rebound to the incident contact speed:

(5)      e_x = (Rω₂-v_x2) / (v_x1 - Rω₁)

e_x has values between -1.0 and 1.0. If e_x is < 0, the ball slides throughout impact. If e_x > 0, the ball grips the surface. If e_x = 0, then v_x = -Rω and the ball is rolling at take off. This is rarely, if ever, the case. e_x is typically less than or greater than 0, meaning spin is either a bit less than (underspin) or greater than (overspin) the spin limit. Like S₂, e_x is a good indicator of whether or not grip occurred during impact. If it did not, maximum spin was not achieved.

2. The Experiment

An inexpensive 1.0 mm table tennis rubber with no sponge layer and pips side up was secured to a Yonex Vcore MW pickleball paddle. The paddle was secured to a solid aluminum incline that could be adjusted to 0-90 degree angles from the horizontal. Balls were fired at an average speed of 6.3 m/s (14.1 mph) and spin of -481 rpm. The incident angle of impact was altered between 10 and 80 degrees. Impacts were videoed at 300 fps and exported to Tracker motion analysis software. Both the paddle with and without the rubber were tested in order to compare the difference.

3. Results

Figure 3 shows that the spin was almost doubled with the rubber surface compared to non-rubber one. It was also substantially higher than predicted by the theoretical friction spin limit.

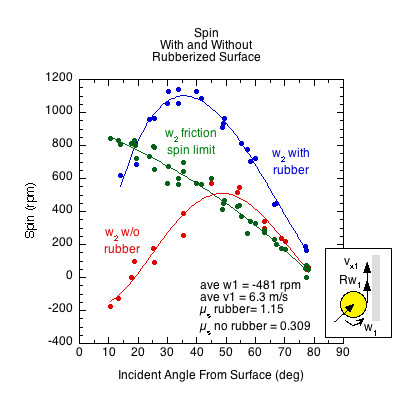
Figure 3 — Elastic spin vs friction-only spin vs theoretical friction spin limit. The three curve fits are for (1) the theoretical maximum spin if Rω₂= -v_x2 during impact, (2) curve fit for the actual spin generated from the tangentially elastic rubber hitting surface, and (3) the curve fit for the paddle without the rubber surface.

The ball bounced from the non-rubber surface with overspin for impacts between 50 and 90 degrees (i.e., the angles at which the ball gripped the surface and achieved the spin limit). At angles below 50 degrees from the surface, the spin from the non-rubber paddle fell below the friction spin limit curve, meaning that the ball slid throughout impact. The elastic response of the rubberized surface far exceeded the friction-only spin limit at all angles except below about 15 degrees where the ball slid throughout impact.

Figure 4 compares the tangential energy return (e_x) of the non-rubber and rubber paddles. e_x for the non-rubber paddle hovers just above 0 at all angles where the ball grips the surface. Just as S₂ = 1 is the condition of gripping the surface, so too is e_x = 0. For the non-rubber paddle, where e_x is above 0, the ball gripped the surface and bounced with a bit of overspin. Where it is below 0, the ball slid throughout impact and did not achieve the friction spin limit. The energy return of the rubber surface is so great because not only did the rubber snap-back add to spin, but it also reversed the direction of the bounce. At all angles above the rubber surface peak e_x, the velocity parallel to the paddle (v_x) reversed direction (i.e., energy was returned). By referring to Figure 3, it is seen that peak spin occurred at the same angle as peak e_x.

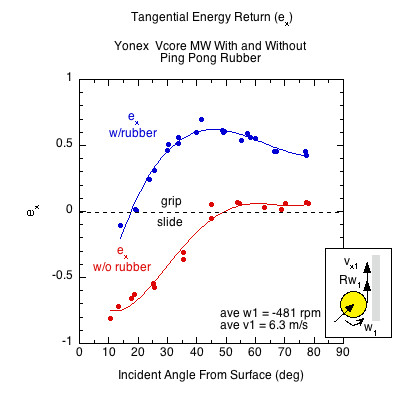
Figure 4 — Tangential Energy Return Curve fits for tangential energy return (e_x) for both the paddle with and without the rubber surface.

Figure 5 shows that the average coefficient of restitution (COR) for the rubber paddle was 0.731 and 0.641 for the non-rubber paddel. That means that perpendicular to the paddle, the rebound speed will be 14% faster from the rubber surface. The corresponding energy return is given as 100 x (e_y)² — i.e., 53.4% for the rubber surface and 41.1% for the normal paddle. For most impacts of concern, the COR is independent of incident angle, spin and speed. COR does decrease at very high impact speeds however and, as indicated in the graph, it appears to decrease at very low angles.

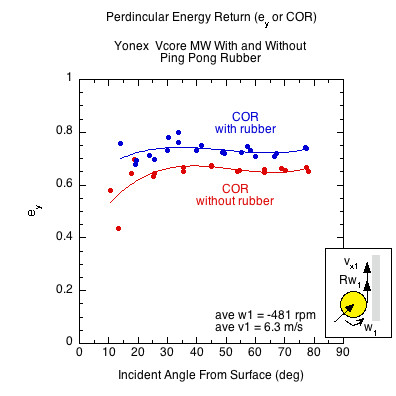
Figure 5 — Coefficient of Restitution. The coefficient of restitution (e_y) is higher at all impact angles for the rubber-surfaced paddle.

4. Discussion

The prohibition against "excessive spin" is enforced by compliance to certain lab tests. Disqualification occurs if the surface roughness as measured by a Starrett SR160 Surface Roughness Tester is greater than 30 micrometers for average height from peaks to valleys and maximum height of 40 micrometers from peaks to valleys. It is further specified that the coefficient of kinetic friction cannot exceed 0.1875 as determined by friction tests following the protocol of the ASTM D1894-14 test method [2].

This study, and more especially the study Pickleball Spin: The Role of Surface Roughness in Spin Generation, suggests that perhaps the rules and testing methods should be re-examined. First, measuring the surface roughness of the paddle alone, independent of the ball, does not necessarily correlate to how the ball and paddle will interact with each other. Surfaces have to be measured in motion against each other. The Starrett roughness tester only measures the paddle. Traditional static and kinetic friction testing methods (sliding the two surfaces against each other) do just that, but it is unclear whether the association's use of ASTM protocol involves the ball and paddle surfaces sliding on each other or just the paddle sliding on a given test material (e.g., a plastic film).

Friction is the primary driver of spin for paddles as presently manufactured. That being the case, five findings of this study argue against the roughness and coefficient of friction rules as presently administered. First there is a friction-generated spin limit that is the same for all paddles for all impacts with the same incident parameters. Second, most paddles achieve the spin limit at almost all impact angles commonly encountered in pickleball, no matter their measured coefficient of friction. Third, for any given set of incident parameters, every paddle has a maximum angle (measured from the surface) at which it will achieve the spin limit. Below that angle (i.e., more oblique angled impacts), the spin will be less. Furthermore, for most paddles, the maximum angle is below any incident angle typical in play. Fourth, as a result, in almost all circumstances, all paddles will generate the same spin at all impact angles typically encountered in play. Fifth, paddles with higher coefficients of friction do indeed generate more spin at angles where both paddles are below their maximum spin angle, but that spin does not achieve a magnitude equal to that achieved at higher angles. In that sense, a higher COF certainly does not threaten the nature of the game.

Those considerations are based solely on experiment and physics. As in all sports, perception, which is presumptive, subjective, and non-quantifiable, is the prime driver in performance assessments. On court, power, spin, control, and comfort are an amalgamation of sound, feel, and shot results. These may or may not be in agreement with measurements of those same shots. Also, and more important, the speed, spin, and angle of your opponent's incoming shot determines the characteristics of your shot to a very great degree. The perception of the paddle's performance is difficult to separate from the effects of your opponent's shot on the ball-paddle interaction. This in large part dictates the speed and spin of your return. (Note: the speed and angle of your swing determines the shot more than anything, but in this experiment, that is all figured by the statement "for any given set of incident parameters".)

5. Conclusion

The spin from the rubber surface was almost double that of the normal paddle and the rebound 14% faster. This was true at all incident angles. Paddles without elastic surfaces create about the same spin at all incident angles where the ball grips the paddle and achieves the theoretical spin limit. The coefficient of friction between the ball and paddle does not matter in those cases. At angles where two paddles do not achieve the spin limit, the paddle with the greatest coefficient of friction will create the most spin, but it will not be as much as it achieves in its gripping range of angles higher up from the surface.

The performance of the rubber-surface paddle is far superior in rebound spin and velocity (power) than a non-rubber paddle. For players, performance is easy to equalize just by getting a similar paddle. But the question at hand is not so much about fairness but about whether allowing rubber-surfaced paddles would negatively change the nature of the game. This study was simply to show the difference between paddles. The answer as to whether this is a "good" or "bad" difference is beyond the scope of this study.

However, based on the experimental results presented here (and here), it might be beneficial to revisit the rules, tests, and implementation regarding paddle surface friction.

6. References

[1] C. Lindsey, "Pickleball Spin: The Role of Surface Roughness in Spin Generation", href="https://twu.tennis-warehouse.com/learning_center/pickleball/pickleballspin.php".
[2] USA Pickleball, "2021 Equipment Standards Manual", https://usapickleball.org/docs/eec/Equipment-Standards-Manual.pdf.