1. ABSTRACT
This research looks at the role of friction between the ball and the strings in spin generation. Several qualitative experiments were performed to see friction in action between string and ball and to observe the effects on spin. Also, experimental procedures were developed to measure the friction between the string and ball for the ball's motion both parallel (cross strings) and perpendicular (main strings) to the length of the string. The conclusion is that strings with maximum perpendicular string-to-ball friction and minimum string-to-string friction will produce the most spin. Previous Tennis Warehouse University (TWU) research on the role of string friction on spin can be found at the following links:
2. INTRODUCTION
String manufacturers have always marketed tennis strings according to their ability to grip the ball via sticky coatings, rough/grabby surfaces, or "biting" shapes. The underlying theory is that greater friction between the string and the ball will cause more spin.
This was universally accepted as true until it was demonstrated that for all impacts less than 50 degrees away from perpendicular, the strings will bite the ball to the maximum extent possible, no matter the texture, shape, or material of the string. This is important because when biting occurs, friction ceases. This result assumes that the stringbed is laterally rigid — i.e., the strings do not move sideways, or, if they do, they do not snap back into position. This was the situation in the pre-polyester string days. As we will see below, polyester changed everything.
Sliding, Biting, Rolling (no lateral string movement)
The biting process is as follows: at impact the ball slides across the strings with backspin and friction slows and rotates the ball. At the ball's contact point with the strings, both its linear motion and direction of spin are the same. Friction reverses the rotation direction so that the linear motion is forward and the rotational motion is backward at the contact point. When friction causes the linear and rotational speeds relative to the strings to become equal and opposite, the contact point is then at rest, and thus, there is no longer any motion-resisting frictional force. If all strings were to produce this same result, then they would all produce the same spin.
The slow motion (240 fps) videos in Movie Screen 1 demonstrate the process.
Choose Movie
Movie Screen 1 —Sliding, biting and rolling for three materials. The ball begins with backspin, slides, changes to topspin, bites, and begins to roll at constant spin. Friction ceases as the ball goes into rolling mode and no more spin is imparted. The braided nylon/zyex string (first video) achieves rolling sooner than the others. The slipperier polyester in the second video achieves the same final spin but takes longer to do so. In video 3, the braided string in back produces higher friction, so in addition to topspin, a sidespin is generated.
After the ball is set in motion, ignoring air resistance, the only significant net force is friction generated between ball and string. The string in the first video is a braided with a rough textured exterior that produces high friction, and the string in the second video is a smooth polyester with low friction. Both strings reach the same spin rate (approximately 80 rpm), but the rougher string accomplishes this in a shorter time. However, during a tennis hit, there is enough friction generated in the 5 ms impact duration to bring the ball to bite for both strings. Thus, the ball rolls for a longer time on the rough string than on the smooth string, but they both rebound while rolling (spinning) at the same rate. If this were the end of the story, string-to-ball friction would not matter for most tennis shots.
Sliding, Biting, Rolling (with lateral string movement)
But this conclusion only applies if the main strings do not slide sideways across the cross strings. If sliding occurs, which is a dominant effect of using polyester, then additional spin will be imparted by the sideways snap-back of the string. It used to be assumed that the main string movement was undesirable because the strings did not snap back and would get stuck out of position. This was a waste of elastic energy, as well as an annoyance to rearrange strings between points. But recent research has shown that main strings do move and snap back — how far, how fast, and with how much energy depending on the string's stiffness and the friction between the mains and crosses. A string that has a low coefficient of friction between strings will commence, sustain, and reverse its sideways slide more easily, optimizing the timing of the snap-back and losing less energy in the process. In this phase of spin generation, low inter-string friction is key.
But, string-to-ball friction is important here also. If there is greater string-ball friction, then the ball can laterally move the main string farther and faster, giving it more energy and time with which to snap-back. And here too, string-ball friction is important, because the string that grabs onto the ball with the greatest force will most efficiently increase the torque generated by the snap-back.
3. String-To-Ball Friction — Observational Experiments
Beam Drop Experiment
In order to observe the mechanisms of string-ball friction during snap-back, three related experiments were created. First, a 1" x 1" beam with tennis cloth glued to two sides was dropped between two strings in parallel, pulled to 35 pounds. The goal was simply to film and observe the nature of the interaction between the tennis cloth and the string. The first movie in the drop-down menu in Movie Screen 2 shows the setup and movement of the beam between polyester strings at 240 fps. The second and third movies, respectively, are close-ups at 1000 fps of a polyester and a braided nylon.
Choose Movie:
Movie Screen 2 — Tennis Cloth-String Interaction. The movement of the string on the ball is jerky (slip-stick behavior) in all cases and the more friction there is, the slower the beam drops.
The cloth covered beam allows us to macroscopically observe over distance and time what is happening at microscopic distances and time. The slip-stick behavior evident in the videos might be partially responsible for the spin variance often observed in shots with nominally identical input parameters.
Dueling Main Strings Experiment
In the second experiment, shown in Movie Screen 3, two parallel strings (one in front and one in back) were each pulled to 20 pounds by hanging kettle bell weights. Each of the two strings could be the same make, material, shape, or texture, or they could be different. The strings were separated and a ball placed between them. This increased the tension to about 40 pounds on each string. A plunger device was rigged to smash down on the top of the ball, pushing the ball through the two strings. Movie Screen 3 shows several combinations using a different string in the front and the back. This allows us to simultaneously see how each reacts under the same force. These movies were filmed at 1,200 fps. Depending on the video, the strings begin to release and snap back in about 4-10 ms, just as in a racquet impact.
Choose Movie:
Movie Screen 3 — Main string interaction with ball. Spin is or is not induced depending on the friction between each string and the ball and which string releases its bite last. If the same string is in the front and back, the strings release simultaneously and no spin is generated. If the strings are different, the string generating the most friction with the ball will hold longer and spin the ball.
(Note: To see details of rapid movement, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
The first movie in Movie Screen 3 shows the spin result of the same string (smooth polyester) on each side of the ball (back and front to camera). In this case, both strings release their grip on the ball at the same time and with equal force so there is no net torque exerted on the ball and thus no spin.
In the second movie, the front string is a smooth polyester (Tourna Big Hitter Blue) and the back string is a rough, braided nylon (Ashaway Dynamite Soft). In this case, the polyester released first and the braided nylon then exerted spin-creating torque, giving the ball topspin toward the camera.
The third movie reverses the situation in movie 2, placing the polyester in back and the nylon in front. This was done to make sure that it was the string causing the spin and not some artifact of the experimental setup. The same sequence of events occurred and the ball left the strings with topspin away from the camera — i.e., the opposite direction as with the strings reversed.
Dueling Main Strings with Crosses Experiment
The third iteration of this experiment involved adding a pair of cross strings to each lateral side of the ball. The plunger now forced the ball to push against the mains, moving them across the crosses, just as occurs in tennis hit. The main strings simultaneously maintained their grip on the ball until one or both strings released, resulting in the expected spin. The three videos in Movie Screen 4 all have the same polyester (Signum Pro Poly Plasma Pure) installed as the cross string. The front and back main strings in the first video are both polyester. The second video shows polyester in front and braided nylon in back. The third video reverses video 2 — braided nylon in front and polyester in back.
Choose Movie:
Movie Screen 4 — Mains, crosses and ball interaction. The ball pushes the main string over the crosses. The mains release separately or together, creating or not creating spin respectively.
(Note: To see details of rapid movement, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
In these videos (also filmed at 1,200 fps), the result is essentially the same as without the cross strings in Movie Screen 3 — the polyester releases first and the braided, rough nylon spins the ball. In this case, however, when the first main and its crosses release, the remaining main and crosses also push the ball forward or backward. These videos are evidence that different string types interact differently with the ball, producing different results.
The videos are stunning displays of how different strings interact differently with the ball but are not meant to be used for comparative purposes. For that, we need to make some measurements.
4. MEASURING STRING-TO-BALL FRICTION
When the ball moves across the stringbed it moves parallel to the cross strings and perpendicular to the mains. Thus, two experiments were devised to measure the friction in each direction. In each experiment, we will determine the coefficient of friction (COF) of each string.
Friction Parallel to the String
The equation for friction is F = μN, where F is the friction force, N is the normal force pushing the two surfaces together and acting perpendicular to those surfaces, and μ is the coefficient of friction (COF), which is the constant of proportionality between the friction force and the normal force. μ is the "stickiness" factor. It will depend on the molecular attraction between surfaces, the surface typographies, and the relative stiffness/hardness of the surfaces. These factors determine how readily two surfaces will slide across each other. μ will vary depending on the experimental setup and input parameters, but the relationship between the various materials tested should remain the same independent of setup and parameters.
To measure the string-to-ball COF parallel to the string, a string incline was created by hanging a 20 lb weight from two parallel strings spaced about 30 mm apart. The incline was set to 57 degrees. This steep angle was chosen to make sure that the ball would slide all the way down the incline. This is a necessary condition of the experiment. Gravity continuously accelerates the ball faster than friction can slow and spin it (especially because the only force pushing the string and ball together is the weight of the ball), so biting and rolling never occurs, and the ball slides all the way down the incline. Therefore friction acts throughout the trip down the incline so we can then use beginning and ending velocities and spins to determine the effects of friction in-between. At lower angles, depending on the COF, the ball might begin to roll for portions of its trip. For example, if the COF parallel to the string were 0.3, rolling would occur even at 40 degrees.
The slide down the string incline was filmed at 120 fps and the spin and velocity were measured at the very end of the incline. The incline length was 545 mm. Movie Screen 5 shows the setup and a typical slide down the incline.
Movie Screen 5 — String incline to measure string coefficient of friction. The speed and spin is measured at the end of the 545 mm incline and the COF is calculated with the help of the formulas in Figure 1 below.
(Note: To see details of rapid movement, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
Figure 1 shows the geometry and some of the math used to arrive at the string-to-ball COF parallel to the string.
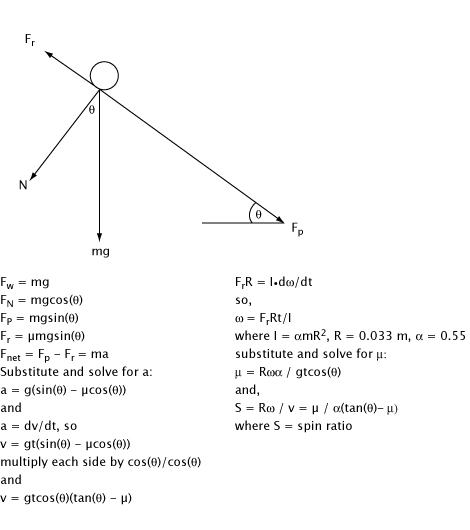
Figure 1 — Geometry and calculations used to obtain the string-to-ball COF parallel to the string.
Table 1 displays the results of several strings of different material.


Friction Measurements Parallel to the String
| Brand | String | Material | Spin (rpm) | Spin Ratio (S=rw/v) | Friction (N) | Ave. Velocity (m/s) | COF |
|---|---|---|---|---|---|---|---|
| Ashaway | Dynamite Soft 17 | Zyex/Nylon | 307 | 0.38 | 0.085 | 2.83 | 0.279 |
| Polyfibre | TCS Rapid 1.25 | Polyester | 190 | 0.25 | 0.055 | 2.67 | 0.181 |
| Prince | Recoil 16 | Nylon | 184 | 0.23 | 0.055 | 2.77 | 0.179 |
| Babolat | VS Touch 16 | Gut | 168 | 0.22 | 0.051 | 2.67 | 0.167 |
| Prince | Synthetic Gut Original 16 | Nylon | 166 | 0.2 | 0.047 | 2.83 | 0.154 |
| Wilson | Natural Gut 16 | Gut | 154 | 0.18 | 0.045 | 2.9 | 0.149 |
| Babolat | Excel 16 | Nylon | 140 | 0.18 | 0.041 | 2.73 | 0.136 |
| Prince | Synthetic Gut w/Duraflex 17 | Nylon | 140 | 0.18 | 0.040 | 2.73 | 0.132 |
| MSV | Hepta-Twist 1.25 | Polyester | 137 | 0.16 | 0.039 | 2.88 | 0.129 |
| Solinco | Vanquish 16 | Nylon | 130 | 0.16 | 0.038 | 2.79 | 0.123 |
Table 1 — Friction measurements parallel to string at 57 degree incline.
It is evident from looking at the spin column that different strings can generate more or less spin, at least when the ball slides throughout contact with the strings so that friction is continuously exerting a torque. The spin ratio (S) is the ratio of the rotational speed at the contact point to the linear speed. S = 1.0 means that the speeds are equal and opposite such that the speed relative to the strings is 0, there is no friction and the ball is in rolling mode. Spin ratio below 1.0 indicates that the ball slides throughout the contact time. On very oblique stringbed angles to the ball (greater than 50 or 60 degrees from perpendicular), the ball will slide the entire contact time.
Friction Perpendicular to the String
But friction parallel to the cross strings may be different than friction perpendicular to the main strings. The bumps, obstacles, roughness and elastic resistance encountered by the ball are the result of the main strings, which the ball slides over perpendicular to the string. The net friction forces will be a combination of the friction of both the mains and crosses.
To measure the coefficient of friction perpendicular to the mains, a variation of the above incline method was used. A 2.25-inch (60 mm) diameter PVC pipe was fitted with a tennis ball. A length of string was cut and looped over the ball and a 6.3 lb (2.86 kg) weight was hung on the string. The incline was gradually raised using the crank on the tripod base until the string slid off the ball. The incline angle was measured at string release from the ball. Figure 2 shows the basic setup.

Figure 2 — Test setup for measuring friction perpendicular to the main strings.
The friction force is greater perpendicular to the string than it is parallel for the main reason that the string sinks into the ball and has to climb out of the groove in order to slide, whereas for parallel movement, the string slides in the groove. Ball deformation becomes a much larger factor in the magnitude of friction in the direction perpendicular to the mains.
The method for calculating the coefficient of friction is as follows. As the incline is raised, there will be a component of the mass on the string perpendicular to the incline, FN, and a component force parallel to the incline, Fp. Up to a point, static friction will exactly resist the the force parallel to the incline and hold the string on the ball. At a certain angle, the static friction force, Fr, will reach a maximum for the materials in contact, and the string will release. Fr is equal to the coefficient of friction, μ, times the normal force, FN. Thus, the coefficient of friction is calculated by dividing the friction force by the normal force. As it ends up, this is simply the tangent of the measured incline angle. The details are presented in Figure 3.
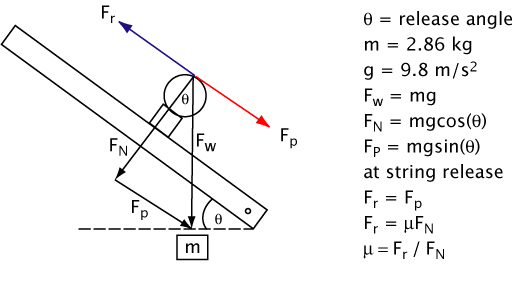
Figure 3 — Diagram of test setup and calculations for measuring the coefficient of friction perpendicular to the main strings.
Table 2 presents the results for several strings.
| Table 2 COF Between Ball and String Perpendicular to String | ||||
|---|---|---|---|---|
| Brand | String | Material | Surface | COF |
| Solinco | Barbwire 16 | Polyester | Textured | .543 |
| Ashaway | Dynamite Soft 17 | Nylon | Braided | .527 |
| Tecnifibre | NRG2 18 | Nylon | Coated | .514 |
| Prince | Top-Spin Plus 16 | Nylon | Textured | .512 |
| SuperString | Viper V2 Rough 16L | Polyester | Textured | .486 |
| MSV | Hepta-Twist 1.25 | Polyester | Shaped | .481 |
| Tecnifibre | XR3 1.25 | Nylon | Coated | .475 |
| Alien | Black Diamond 16 | Polyester | .473 | |
| Dunlop | Hexy Fibre 17 | Nylon | Shaped | .466 |
| Babolat | Hurricane Feel 16 | Polyester | .464 | |
| Klip | K-Boom 16 | Polyester | .464 | |
| Tecnifibre | X-1 Biphase 1.24 | Nylon | Coated | .464 |
| Signum Pro | Tornado 1.29 | Polyester | Shaped and Twisted | .462 |
| Topspin | Cyber Blue 17 | Polyester | .458 | |
| Luxilon | ALU Power Spin 1.27 | Polyester | Shaped | .454 |
| Yonex | Tournament 80 Spin 1.28-1.38 | Nylon | Contour wrapped | .451 |
| Luxilon | Big Banger Timo 1.17 | Polyester | .443 | |
| Head | Fibergel Spin 1.30 | Nylon | Contour wrapped | .439 |
| Mantis | Comfort Poly 16 | Polyester | .437 | |
| Gamma | Asterisk Spin 16 | Nylon | Twisted | .433 |
| Wilson | Sensation 17 | Nylon | Coated | .431 |
| PolyFibre | Hexablade 16 | Polyester | Shaped | .429 |
| Mantis | Power Poly 1.25 | Polyester | .42 | |
| Prince | Synthetic Gut Original 17v | Nylon | .42 | |
| PolyFibre | TCS 1.20 | Polyester | .418 | |
| Tecnifibre | Pro Red Code 1.20 | Polyester | .416 | |
| Prince | Synthetic Gut w/Duraflex 17 | Nylon | .414 | |
| Luxilon | Big Banger Original Rough 1.30 | Polyester | Textured | .406 |
| Solinco | Vanquish 1.30 | Nylon | .404 | |
| Gamma | Zo Twist 16 | Polyester | Shaped and Twisted | .4 |
| Signum Pro | Poly Plasma Pure 1.18 | Polyester | .392 | |
| PolyFibre | TCS Rapid 1.25 | Polyester | .384 | |
| Gosen | Polymaster II 16 | Polyester | Shaped | .374 |
| Prince | Poly Spin 3D 1.27 | Polyester | Shaped | .374 |
| Volkl | Gripper 1.25 | Nylon | Textured | .372 |
| Babolat | Excel 16 | Nylon | .358 | |
| Babolat | Pro Hurricane Tour 16 | Polyester | .358 | |
| Kirschbaum | SuperSmash Spiky 1.20 | Polyester | Textured | .352 |
| Tourna | Big Hitter Blue | Polyester | .342 | |
| Babolat | VS Touch 16 | Gut | .34 | |
| Weiss Cannon | TurboTwist 1.24 | Polyester | Twisted | .335 |
| Prince | Recoil 16 | Polyester | Shaped | .331 |
| Wilson | Natural Gut 16 | Gut | .331 | |
| Gosen | CompositeMaster II 1.00-1.45 | Polyester | Shaped | .313 |
Table 2 — COF Static Friction Measurements Perpendicular to String.
Each string was tested five times and the average COF was calculated. The string was placed at the apex of the ball's curvature on each trial. The ball was rotated slightly after each string to prevent any permanent grooves from forming. All irregular seam orientations were avoided, as were tests on logo ink (which, in a small independent test, raised the COF slightly). A variety of materials and surface conditions were chosen to get a good cross-section of strings on the market.
5. DISCUSSION / CONCLUSION
For strings tested in both Table 1 and Table 2, it is evident that the COF for movement perpendicular to the string is much greater than that parallel to the string. Essentially, this is to say that the friction between the main strings and the ball is greater than that between the crosses and the ball. The difference is dramatically displayed in Movie Screen 6. The first video is of a ball bouncing on a string rig with cross strings only and the second video is of main strings only. Notice that in the cross string video, there is not enough friction to reverse the backspin into topspin. The main string video does reverse the spin. Keep in mind, however, that the spin created by the main string is both from the friction and the lateral string movement and snapback.
Choose Movie
Movie Screen 6 — Videos of ball bounce from crosses only and mains only. The friction between the crosses and the ball (video 1) is not enough to reverse the ball's spin. Video 2 shows main strings reversing spin with a combination of friction and torque supplied by string snapback.
(Note: To see details of rapid movement, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
In summary, the ball impacts, slides, bites and friction ceases. As the ball slides, it also pushes the main string in the direction of its motion. It will push the string farther and store more energy the more friction there is between the ball and the string and the less friction there is between the strings. Upon snapback, the string begins to slide against the ball in the opposite direction, reactivating the friction force. At this point, the greater the friction between ball and string, the more the ball will be slowed parallel to the the stringbed, the spin will be increased, and the angle of rebound will be increased.
That being the case, the greatest spin should be generated from strings with high string-to-ball friction and low string-to-string friction. Do such strings exist? Yes. The way to find these strings is to look up the strings in Table 2 with the String Friction Tool. It is easiest if you first click the "hide hybrids" button. Immediate examples meeting our requirements on both lists are MSV Hepta-Twist 17, Babolat Hurricane Feel 16, Klip K-Boom 16, Alien Black Diamond 16 and SuperString Viper V2 Rough 16L. Undoubtedly, there are others and Table 2 is a very short list of data compared to the string-to-string database. (Note: the String Friction Tool will eventually have data on all types of friction available.)
It is interesting that there is no predictable correlation between the string surface condition and the COF. This is true for both string-to-ball and for string-to-string friction. But it is true that the top performers in each category are shaped, textured or coated. Thus, it would seem that the ultimate spin string (i.e., maximum spin generation) involves maximizing string-to-ball friction while minimizing inter-string friction. The data above demonstrates that this is indeed possible.



