1. Introduction

The physical properties of ice hockey sticks are described on many web sites, and include things such as weight, length, flex, flex point, kick point, feel, durability, balance, power, release time, and so on. There are a lot of variables to consider if a player is trying to choose a good new stick or is attempting to compare the performance of different sticks. The significance of each of those properties is often a matter of personal preference, but can be evaluated in more detail by considering the physics of hitting a hockey puck. Starting with the simplest ideas first and then working out more technical details, it is possible to figure out which are the most important properties and which are the least important. To that end, we will consider three different hockey stick models in turn, starting with the simplest first.

2. Constant Force Model

The primary objective of hitting a puck with a stick is to project the puck at whatever speed the player wants and in whatever direction he or she wants it to go. To do that the player needs to exert a force on the puck. If a constant force F is applied for a short time T, and if the puck has mass m and is initially at rest, then the puck will accelerate to a speed v given by v = aT where a = F/m is the acceleration of the puck. For example, if F = 100 N, T = 0.04 s and m = 0.17 kg, then a = 588 m/s² and v = 23.5 m/s. Given that the acceleration to to gravity is 9.8 m/s², the acceleration of a puck is huge by comparison. A higher puck speed will result if the force on the puck is increased or if the force is applied for a longer time. That should be intuitively obvious, but the numbers and units involved may not be familiar to some readers.

In physics, 1 meter = 3.28 feet, 10 m/s = 22.4 mph, 1 kg = 1000 gram = 2.205 lb and 10 Newton = 2.25 lb force.

The numbers here are typical in ice hockey, and are easy to understand, but I suspect that most players and coaches rarely think about the game in these terms. Nevertheless, it helps to understand the basic physics if you want to understand what happens when you strike a hockey puck.

In the above example, the puck traveled a relatively long way before the stick stopped pushing it. The distance S traveled during the time T is given by S = 0.5aT ². In this case the puck traveled a distance of 0.47 m. If you double the force to 200 N, and apply it for the same time, then the puck will reach twice the speed and will travel twice as far in getting up to speed. Alternatively, if you double the time while pushing the puck, maintaining the same force, then the speed will double and the distance traveled by the puck will increase by a factor of four.

Another way of describing the physics is to consider the energy of the puck. Its kinetic energy is 0.5mv ² which is 47 Joules for a 0.17 kg puck moving at 23.5 m/s. The puck acquired that energy by being pushed with a force F = 100 N over a distance S = 0.47 m. The work done was FS = 100 x 0.47 = 47 Joules, so the kinetic energy was also 47 Joules. That is a simple example of the "Work-Energy" principle in physics.

That is the essence of getting the puck up to speed. Flex, balance point, stick weight, feel and most of those other things we listed above feature in more subtle ways. A point of interest is that it is the player who does all of the work and who pushes the puck forwards. The stick itself does nothing in the way of useful work. Nothing will happen if the player just holds the stick limply and expects the stick to do all the work. However, the player will have little success if the stick weighs only 50 grams or if it weighs 10 kg or if it is only two feet long. Similarly, a golf club or a baseball bat could be used to strike the puck, but those implements would not work well either. The stick needs to be designed to do the job that it was intended to do, and that includes moving the puck around deftly at low speed by tapping the puck gently. That is why a hockey stick has a light, curved blade rather than a heavy club at the striking end, and why it is five feet long rather than two feet long. In the same way, you could use a screwdriver to strike a nail, but a hammer works better.

Flexing the Stick

There are two basic ways that hockey players can apply a force to the puck. Either way will work and both together work even better. One way is to use the kinetic energy of the moving stick. The other way is to use the elastic energy stored in the stick when it bends. The first way involves hitting the puck, in the same way that a tennis player hits a tennis ball. In that case, the stick is first accelerated by the player and then the stick collides with the puck. As a result, a large force is exerted on the puck for a short time. Energy and momentum are transferred first from the player to the stick and then from the stick to the puck. The process is not very efficient since neither the player nor the stick comes to a dead stop when striking the puck. In that respect, a lot of energy is left over or wasted, but that is the price to pay when heavy arms are used to accelerate a light puck (or a light golf ball, or baseball or tennis ball).

The other way is to bend the stick without accelerating it, in the same way that an archer shoots an arrow out of a bow. In that case, it is elastic energy in the stick that is used to apply a force to the puck, rather than the kinetic energy due to its forward motion. If the stick is pushed against the ice so that it bends, then the stick stores elastic potential energy that can be released when the player is ready. If the stick is lifted quickly off the ice, the stick springs back to its usual straight position and can therefore be used to propel the puck forward.

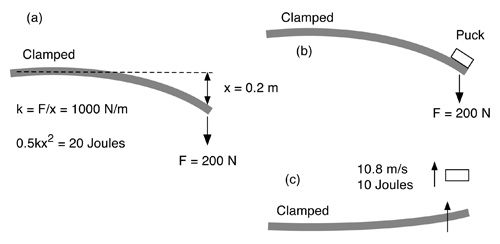
Figure 1 — A hockey stick clamped at the butt end and the middle. A force F is applied at the blade end. If a puck is placed on the blade and if F suddenly decreases to zero, the puck will shoot in the air and the stick will vibrate.

The essential features of stick bending can be illustrated by clamping a horizontal stick to a table, as shown in Fig. 1. If a vertical force F is applied at the blade end, then the stick will bend and the blade will move through a distance x. The distance x is proportional to F, so we can let F = kx where k is the stiffness of the stick. If the length of the overhanging stick is small then the stick will be difficult to bend and k will be large. The stiffness therefore depends on the bending length but is typically about 1000 N/m for a hockey stick held or clamped near the handle end and near the middle of the stick. In that case, a force F = 100 N will bend the stick through a distance x = 0.1 m and a force F = 200 N will bend the stick through a distance x = 0.2 m.

If a puck is placed on the end of the stick in Fig. 1 and the force is suddenly released, the puck will shoot up in the air. The stick will not come to a dead stop when the puck leaves the stick since the stick itself is moving up at maximum speed at that time. The stick therefore overshoots the horizontal position and bends in the opposite direction. The stick will then end up vibrating back and forth after the puck leaves the stick, although those vibrations would be quickly damped by the hands and arms and gloves if the stick was held by hand instead of being clamped to the table.

Movie Screen 1 presents an example of launching a puck this way.

The elastic energy stored in the stick is given by 0.5kx ². For example, if k = 1000 N/m and x = 0.2 m, then the stored energy is 20 Joules. In theory, that energy could be used to launch a puck at a speed of 15.3 m/s since the kinetic energy of the puck would then be 20 Joules. However, part of the stored elastic energy is used to accelerate the stick itself. If the bent section of the stick weighs 0.17 kg, and the puck weighs 0.17 kg, then roughly half the elastic energy will be given to the puck and the other half is used to accelerate the stick.

Suppose that the puck accelerates to 10.8 m/s and ends up with 10 Joules of kinetic energy. It was accelerated over a distance of 0.2 m and traveled that distance at an average speed of 5.4 m/s so it took 0.037 s to reach maximum speed. That is the release time of the stick. The release time can be shortened by using a stiffer stick or by moving the bottom hand closer to the blade so the stick bends over a shorter length.

Suppose that k = 2000 N/m instead of 1000 N/m and the same 200 N force is used to bend the stick. Then x = 0.1 m and the stored energy is 0.5 x 2000 x 0.12 = 10 Joules. To get the same 20 Joules as before, the force would need to be increased to 280 N, giving x = 0.14 m. If the puck is ejected at 10.8 m/s as before, ending up with 10 Joules of energy, then it accelerates over a distance of 0.14 m at an average speed of 5.4 m/s. In that case, the release time is 0.14/5.4 = 0.026 seconds. The player can therefore release the puck sooner with a stiffer stick but has to push harder on the stick to bend it, and ends up with the same puck speed.

The puck speed that can be imparted just by bending the stick is not very large. More commonly, players push or flick the stick forward while bending it, in order to increase the force on the puck. Even higher puck speeds result when the stick is first accelerated and then collides with the puck.

3. Collision Model

A simple collision is shown in Fig. 2 where a heavy object of mass M moving at speed V collides head-on with a lighter object of mass m initially at rest. The heavy object will slow down and transfer some of its momentum and energy to the lighter object. The light object will then take off at speed v due to the force exerted on it by the heavy object. The end result is the same as pushing with a constant force, but when collisions are involved the force does not remain constant. The force starts out at zero when the objects first come into contact, increases to a maximum, then decreases to zero again when the objects lose contact.

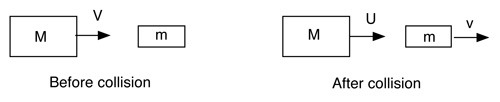
Figure 2 — The collision of a large mass M with a small mass m initially at rest.

Suppose that a hockey stick of mass M collides with a puck of mass m. The stick is first accelerated to some speed V by the player, then the stick collides with the puck. For example, if M = 0.4 kg and V = 20 m/s then the kinetic energy of the stick is 0.5MV ² = 80 J which is more than enough to accelerate the puck to a speed greater than 20 m/s.

The actual speed of the puck can be calculated by assuming that there is no loss of energy during the collision and that the duration of the collision is sufficiently short that the player doesn't have time to add any more energy or momentum to the stick or the puck during the collision itself. That is not quite true, but it simplifies the calculation and the answer is approximately correct.

If the momentum remains constant then

          MV = mv +MU

where U is the stick speed after the collision. If the total energy remains constant then

          0.5MV ² = 0.5mv ² + 0.5MU ²

Another way of stating that the energy remains constant, and one that simplifies the calculation even further, is

          v - U = V

which means that the relative speed after the collision is the same as the relative speed before the collision. In that case, we can solve these equations to show that

          v = 2MV / (m + M)

For example, if V = 20 m/s, M = 0.4 kg and m = 0.17 kg then v = 28 m/s. The puck therefore takes off at a higher speed than the incident stick. The puck gets its energy from the stick, so the stick slows down since it lost energy when it gave it to the puck. Note that we have worked out the speed of the puck without knowing anything about the force on the puck or the time it took to accelerate to that speed, and without knowing anything about how far the stick bent. We don't need to know anything about the stick bending, and it doesn't actually matter how far it bent. The same answer would be obtained if the stick was very stiff or if it was very flexible. It is clear from this result that the puck did not get its energy from the bending of the stick. It got it from the kinetic energy of the stick. The stick had that energy before it collided with the puck and before the stick started to bend.

A question of interest is how we can maximise the speed of the puck. The answer depends on how we vary the other quantities. For example if we keep M and m the same, then the answer is simple. That is, we can increase v simply by increasing V. However, that means we would need to increase the kinetic energy of M so the player would need to do more work. Alternatively, suppose we keep V and m the same and vary M. Then v increases as M increases. Again, the player needs to do more work.

Suppose the kinetic energy of M remains constant. Then the effort expended by the player remains the same. It turns out that v is a maximum when M = m. In that case, the stick would need to be as light as the puck and the stick would come to a dead stop and give all its energy to the puck. However, that is not a practical solution since the player can put more energy into a heavy stick than into a light stick, given that most of the effort of the player is used in swinging the heavy arms. Adding a 400 gram stick to the arms does not slow down the arms very much, so a 400 gram stick will have more energy than a 170 gram stick, with very little extra energy or effort required by the player. A 1 kg stick would have even more energy, the same as a baseball bat, but would be difficult to maneuver into position quickly.

Force Arising from the Collision

Whenever one object collides with another, each of the objects exerts a large force on the other. The magnitude and duration of the force depends on the stiffness of the two objects. If both objects are very stiff then the force will be very large but it will act for only a very short time. If one or both objects are very soft then the force will be small but it will last for a long time. As described previously, the end result depends on FT (force times time) so a large force acting for a short time can accelerate an object to the same speed as a small force acting for a long time. For example, when a baseball bat collides with a baseball, the collision lasts only 0.001 seconds, but a huge force is exerted on the ball. When a hockey stick collides with a rubber puck, the force lasts about 40 times longer and is about 40 times smaller since the stick is much softer than a baseball bat. The puck itself has about the same stiffness as a baseball.

In a bat and ball collision, the very large force squashes the ball and bends the bat. When a hockey stick collides with a puck, the puck squashes slightly and the stick bends due to the force on the stick. The force on the puck is equal to the force on the stick but acts in the opposite direction. As a result, the puck speeds up and the stick slows down.

A similar effect occurs if you drop a ball on the floor. The ball collides with the floor and bounces up again since the force keeps pushing upwards until the ball bounces off the floor. In the process, the ball squashes and then expands back to its original size. However, the ball doesn't bounce simply because it was squashed. That is only part of the story. The kinetic energy gained by the ball as it fell was converted to elastic energy when the ball came to a stop half way through the bounce. The elastic energy was then converted back to kinetic energy when the ball bounced up again.

In a similar way, kinetic energy is given to a stick when the player swings it. During the collision with the ice and the puck, the stick bends as it slows down and stores elastic energy. That elastic energy is then given to the puck. A small amount of elastic energy is also stored in the puck when it squashes, and some of that is released as kinetic energy as the puck loses contact with the stick. However, most of the elastic energy stored in the puck is lost since pucks do not bounce very well. If a puck is dropped from a height of 1 m onto a hard surface and bounces on its edge, it will bounce to a height of only about 0.1 m.

If a force F is applied to the blade of a stick, and if the stick is held firmly by two hands in the usual way, then the blade and the end of the stick will bend through a distance x. For a typical stick, k = 1000 N/m. If F = 100 N then x = 0.1 m. That is a typical force on the blade when it impacts the ice, so the stick will bend by about 10 cm. If F increases to 200 N when the blade strikes the puck then the stick will bend about 20 cm. When the stick bends 10 cm, the elastic energy stored in the stick is 5 Joules. When it bends 20 cm, the elastic energy is 20 Joules. A puck traveling at 30 m/s has 76 Joules of kinetic energy. Obviously, it does not get all its energy from bending and straightening of the stick. It gets most of its energy as a result of the player pushing the stick and accelerating both the stick and the puck. In the process, about 20 Joules is temporarily stored as elastic energy when the stick bends, but most of that is given back when the stick straightens out.

4. Rotation Model

There are three problems with the simple collision model. The first is that the player does not stop pushing the stick when the stick collides with the puck. The player keeps pushing and accelerating the stick throughout the collision. The second problem is that the stick does not move in a straight line. It moves in a circular arc. The third problem is that the puck is struck at the far end of the stick rather than in the middle. All of these problems can be eliminated by assuming that the stick rotates about a fixed axis near the top end and is pushed by the player with a force F near the middle of the stick. The puck is struck at the far end of the stick. To allow for the fact that the stick bends elastically, a spring can be inserted between the puck and the far end of the stick, as shown in Fig. 3.

Figure 3 looks complicated, but it is not. The stick swings about an axis near the top, like a pendulum. However, it differs from a slow-moving pendulum in that it is swung rapidly by the player who exerts a large force F at right angles to the stick at a distance R from the axis. As a result, the stick rotates at angular velocity ω, measured in radians/sec where one radian = 57.3 degrees. Typically, a hockey stick rotates at about 20 radians/s = 1146 degrees/s in a slap shot, or by about 46 degrees in 0.04 seconds.

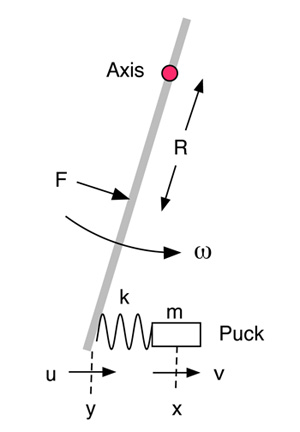
Figure 3 — A stick rotating about a fixed axis. The player exerts a force F at distance R from the axis. The flex of the stick is represented by a spring of stiffness k.

The bottom end of the stick moves to the right at speed u = Lω where L is the distance from the axis to the bottom end of the stick. For example, if L = 1.4 m and ω = 20 rad/s, then u = 28 m/s. The puck has mass m and moves to the right at speed v = dx/dt where x is the horizontal coordinate of the puck. If y is the horizontal coordinate of the bottom end of the stick then u = dy/dt. The spring between the puck and the stick has stiffness k and is compressed by an amount y - x so the force on the puck is F_p = k(y - x). An equal and opposite force is exerted by the spring on the bottom end of the stick.

The equations describing the motion of the puck and the stick are respectively:

          (1)   m(dv/dt) = k(y - x)

and

          (2)   τ = FR - k(y - x)L = I₀(dω/dt) = (I₀/L)(du/dt)

where τ is the torque about the axis and I₀ is the moment of inertia of the stick about the axis.

I₀ is commonly known as the swing weight and is typically about 0.45 kg x m2 for an ice hockey stick. The value of I₀ for a uniform shaft of length L and mass M is ML ²/3 = 0.18 kg x m² if M = 0.3 kg and L = 1.35 m. To that we need to add M_bL_b² = 0.27 kg x m² for a blade of mass M_b = 0.12 kg and L_b = 1.5 m, giving a total value I₀ = 0.45 kg x m² for this particular stick. If the shaft is tapered, with more weight at the handle end and less at the blade end, then I₀ will be smaller.

In Eqs. (1) and (2), it is assumed that the axis is fixed and the player is not moving forwards. If the player is moving forwards at say 5 m/s while swinging the stick, we can simply add 5 m/s to the final puck and stick speed results, even though the actual swing axis will then be in a different location. It is necessary only to change the reference frame, moving along at the same speed as the player, to bring the swing axis back to its assumed, calculated location.