INTRODUCTION

Racquet control is a term that is commonly used to describe the property of a racquet, but it is not a well-defined quantity like balance or swingweight. To some people, control might mean the ability to swing the racquet accurately and easily into position without having to force it to go where you want it to go. To others, control might mean that the racquet helps to control the speed and angle of the ball off the strings. Alternatively, some might argue that it is the player who controls the racquet and the racquet itself does very little to improve control. Nevertheless, it is clear that a racquet that is much too heavy for a young player will be difficult to swing, and a racquet that is much too light will lack sufficient power for an experienced player.

In some cases, it might be possible to quantify control in terms of the physical properties of a racquet. For example, suppose that a player strikes the ball near the frame rather than in the middle of the strings. In that case, the outgoing trajectory of the ball will not be exactly as intended, and the difference will depend mainly on the swingweight or twistweight of the racquet. Even if the player strikes the ball in the middle of the strings, the outgoing trajectory will depend on how fast the incoming ball is spinning and it will therefore depend on how the racquet strings respond to the incoming spin. The outgoing trajectory also depends on the incoming ball speed and angle of incidence on the strings. The effect of a change in the incoming speed and angle will vary, depending on the properties of the racquet. Some racquets might help to control or compensate for undesirable outcomes better than others.

CONTROL EXPERIMENT

Factors that might affect racquet control were investigated by setting up a simple experiment where a tennis ball was fired from a ball machine to impact a hand-held racquet at rest, as shown in Figure 1. The racquet was held vertically, with the tip resting lightly on the floor, and the ball was fired horizontally to impact either near the middle of the strings or closer to the frame but at the same height (nearer the 3 or 9 o'clock positions). The racquet wasn't swung at the ball since it is not easy to control the racquet speed and approach angle precisely, nor is it easy to control the impact point on the strings or even measure it. Those factors were eliminated from the experiment by holding the racquet at rest and varying only the incoming ball speed, incident angle, incident spin and the impact point on the strings.

By filming the results with a video camera, we were able to measure the effects of small changes in those quantities, as well as large changes. Small changes happened automatically since the ball machine was not 100% consistent. Over a period of one week we filmed about 500 different shots using four different racquets. In the end, we focussed on just one of those racquets and varied its properties by inserting two small bolts through the strings at 3 o'clock and 9 o'clock so that we could compare a low twistweight racquet with a high twistweight racquet. We obtained 165 shots for this racquet, and the results are described below.

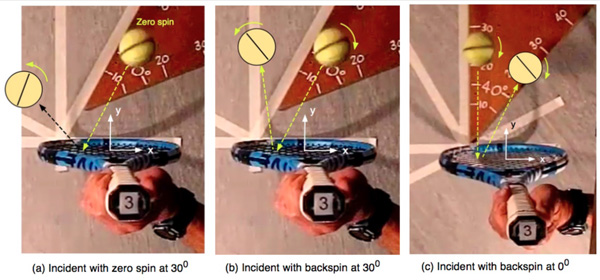
Figure 1 — Ball incident on a racquet initially at rest.

Figure 1 shows the differences that arise when the incident angle and spin are varied. If the ball is incident at right angles to the string plane and without spin, then it bounces more or less at right angles without spin. Nevertheless, small variations arise from differences in string movement, and larger differences arise depending on the impact point on the strings. The ball bounced at low speed if it impacted near the frame rather than the middle of the strings, and it bounced at a higher speed near the middle of the strings or when the bolts were added.

Figure 1(a) shows a typical result where the ball is incident without spin, at 30° to the normal, and impacts towards the frame. The ball bounces with reduced speed (compared with the incoming speed), and with topspin. If the same ball is incident with backspin, as in Figure 1(b), the outgoing topspin is reduced, and so is the outgoing angle to the normal. Figure 1(c) shows an example where the ball is incident at right angles to the string plane, with backspin, with the result that the ball bounces away from the normal and with reduced speed and spin compared with the incoming ball.

EXPERIMENTAL CONDITIONS

The ball launcher contained two counter-rotating wheels that could be rotated at the same speed to launch balls without spin, or at different speeds to launch balls with backspin onto the racquet. Without spin, the incident ball speed was 16.5 +/- 1 m/s, and 74 shots were fired at the racquet at right angles or at 30 +/- 1 degrees away from the normal, with and without the bolts connected. Each bolt weighed 13.4 g, adding 26.8 g to the 291 gm racquet. An additional 91 shots were filmed with backspin at -270 +/- 20 rad/s and at an incident speed 13.5 +/- 0.5 m/s. In both cases, the impact point was varied from x = -80 mm to x = 60 mm, that is from near 9 o'clock to near 3 o'clock.

BOUNCE SPEED

Suppose that a ball is incident at speed 60 mph at right angles to the string plane, and the racquet is initially at rest and hand held as shown in Figure 2(a). If the ball bounces at 18 mph, at right angles to the string plane, then the ratio of those two speeds is 18/60 = 0.3, a number known as the Apparent Coefficient of Restitution, or ACOR. It is given the symbol e_A when used in formulas. The ACOR for a racquet depends on the impact point and is typically about 0.4 in the middle of the strings and about 0.1 or 0.2 near the frame, regardless of the speed of the incoming ball.

The significance of the ACOR is that if a racquet approaches the ball at speed V , and if the ball is at rest instead of the racquet (as in a serve), then the outgoing ball speed is v = (1 + e_A)V . For example, if e_A = 0.4 and V = 70 mph then v = 1.4 x 70 = 98 mph.

Figure 2(b) shows a different situation where the ball is incident at 40° to the string plane and bounces at 30°. The speed of the incident ball is again 60 mph, and its speed in a direction perpendicular to the string plane is 60 x cos 40 = 46 mph. The ball bounces at 16 mph, and its speed perpendicular to the string plane is 16 x cos 30 = 13.8 mph. In that case, ACOR = 13.8/46 = 0.3. That is, the ACOR is the same, provided the ball bounces off the same spot on the strings.

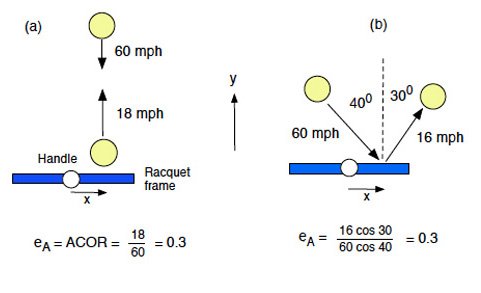
Figure 2 — Definition of ACOR (e_A).

Measurements of ACOR showing all 165 shots are shown in Figure 3, both with the added bolts and without the bolts. The main points of interest are that (a) the ball bounces best near the middle of the strings and not so well near the frame, (b) adding extra mass to the frame results in an increase in ACOR, and (c) the value of ACOR at any given impact point does not depend very much on the speed, spin or angle of the incident ball. Similar results have been observed many times before, with many racquets. The fact that all the data points do not lie on two perfectly smooth curves means that no two bounces are exactly the same and that ACOR depends slightly on the spin of the ball and whether the ball lands on two, three or four strings and whether the strings move sideways in the string plane.

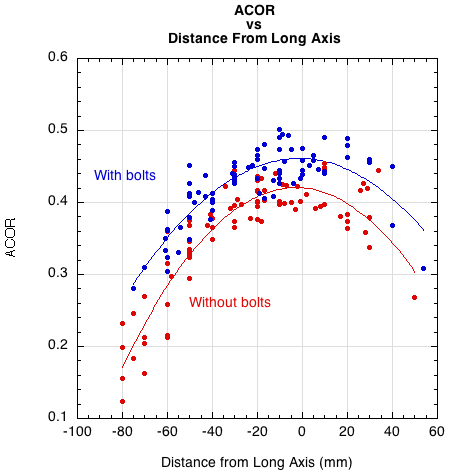
Figure 3 — Measurements of ACOR vs distance from the long axis (x). Smooth curves are fitted to the data points for impacts with and without added mass.

Effective mass (M_e), also known as hittingweight, is another helpful measurement for measuring performance. Each impact location behaves "as if" it were a localized point having the calculated effective mass. Typically, M_e is about one-third the actual racquet weight in the tip, one-half in the center, and equal near the balance point, or center of mass. At any location, the hittingweight (as well as ACOR) will depend on the swingweight and twistweight. The higher the hittingweight, the less the racquet will twist, rotate, and translate and both control and power will increase. Figure 4 shows how ACOR (power) depends on hittingweight.

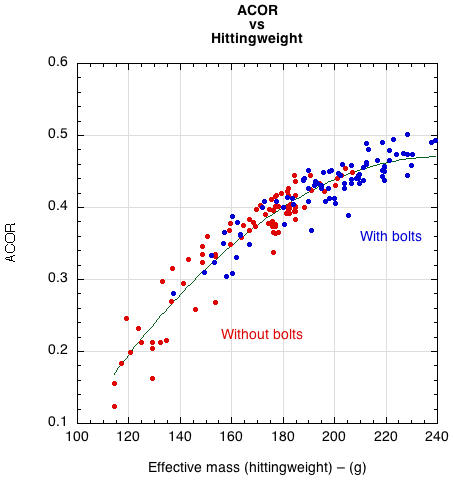
Figure 4 — ACOR vs hittingweight for all 165 bounces, both with and without added bolts.

Adding extra mass to the frame improves the bounce, but then the racquet is harder to swing, so the outgoing ball speed might be about the same in practice. However, it is clear that if the ball is struck near the frame rather than in the middle of the strings, then the outgoing ball speed will be reduced. In that respect, it is the player's fault. Nevertheless, a racquet with extra mass in the head does help slightly, since ACOR does not decrease as much near the frame as it does with a head light racquet. For example, in Figure 3, ACOR is about 0.3 near the frame for the heavier racquet but it is only about 0.2 for the lighter racquet.

When you graph any result against both ACOR and hittingweight, the results look very similar. That is because they both depend on swingweight and twistweight. They are somewhat different ways of looking at the impact however. ACOR measures a result of the bounce and hittingweight is a calculated property that explains the ACOR result. Hittingweight is perhaps the most intuitive parameter for understanding performance results. We will use both below in the discussions on bounce angle and spin.

BOUNCE ANGLE

Unlike the bounce speed, the bounce angle depends strongly on both the angle of incidence and the incident spin. Figure 5 shows the geometry and incident parameters of interest (future figures will reference the impact conditions of Figure 5 — letters "A", "B", "C", and "D").

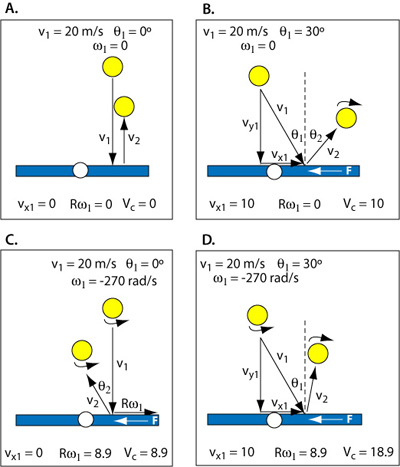
Figure 5 — Incident geometry and parameters (velocity units are m/s). Friction acts opposite the tangential speed of the ball relative to the racquet (V_c) where V_c = v_x1 + Rω₁, where v_x1 is tangential component of v₁ and Rω₁ is the tangential spin speed.

In Figure 5, v_x1 is the incident velocity component tangent to the strings, Rω₁ is the tangential speed of the spinning ball, where R is the radius, and V_c is the contact velocity tangent to the strings where V_c = v_x1 + Rω₁. Friction acts opposite the direction of V_c and its duration depends on the magnitude of V_c. Under most circumstances, friction acts both to slow the ball and to change the spin in the direction opposite that of the incident spin. However, friction can sometimes act to increase incident tangential speed (as in the bounce of a topspin lob) and spin (as in any slice shot). Slowing the tangential speed of the ball decreases (makes closer to the perpendicular) the rebound angle. In Figure 5A, there is no friction, so there is no change in spin or direction of the rebound. In Figure 5B, friction decreases v_x1 and turns it into topspin. In Figure 5C, the ball has no linear tangential incident velocity (v_x1 = 0), but it does have tangential spin speed. Friction acts to decrease the spin and push the ball backwards, thus the negative rebound angle. And in Figure 5D, V_c is large due to both v_x1 and Rω₁ being in the same direction. Friction slows the ball and reverses spin until v_x and Rω are equal and opposite so V_c = 0, sliding stops, and the friction force drops to zero.

Figure 6 displays the rebound angle vs ACOR. For impact group A (30°, no spin) and D (0°, -270 rad/s spin), as ACOR increases both due to impact location and to the addition of the bolts, the rebound angle is closer to the perpendicular, indicating more control. When a player strikes a ball, he or she normally expects the ball to head off in a direction perpendicular to the string plane, or at least in the same direction that the racquet head is moving. If it doesn't then that indicates poor control. Surprisingly, the bounce for group D with both incident angle and spin is almost the same as in group A where there was no tangential speed or spin. Since V_C is relatively large in D, the friction force acts for a long time while the ball slides across the strings. As a result, the horizontal speed of the ball drops almost to zero, so the ball rebounds almost perpendicular to the string plane.

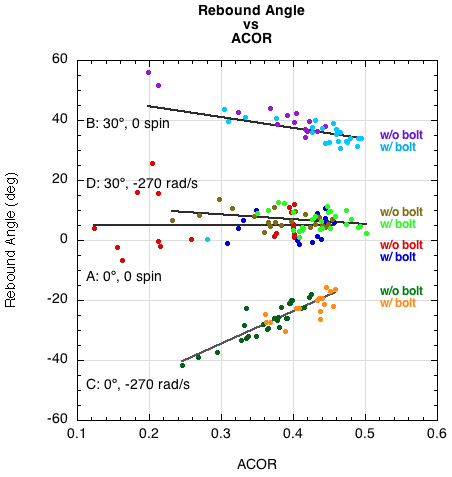
Figure 6 — Bounce angle θ₂ vs ACOR for all 165 bounces, both with and without added bolts.

Figure 7 shows the dependency of rebound angle on hittingweight. This is essentially the same result as in Figure 6 but displayed in units that are more familiar to most readers — grams. Here again we see that adding bolts decreases the rebound angle, except for groups A and D which are effectively zero angle, zero spin incidence and rebound.

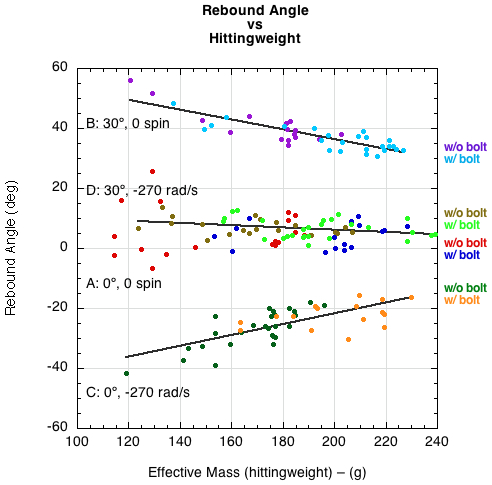
Figure 7 — Bounce angle θ₂ vs hittingweight (impact conditions A and D have here been fit to one curve since the results are so similar).

Figure 8 is another equivalent view of the same results. This graph plots the rebound angle vs the impact distance from the longitudinal axis. The efficacy of the bolts for minimizing rebound angle is apparent.

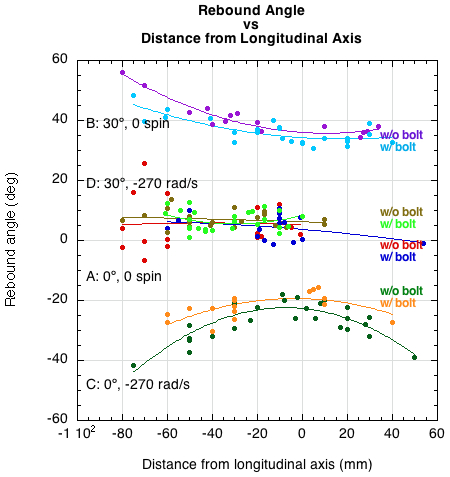
Figure 8 — Bounce angle θ₂ vs impact distance from longitudinal axis.

BOUNCE SPIN

The rebound spin, ω2 is shown in Figure 9 vs ACOR and Figure 10 vs M_e. The spin does not depend strongly on either, although the spin does decrease as ACOR and M_e increase when the ball is incident without spin at θ₁ = 30°.

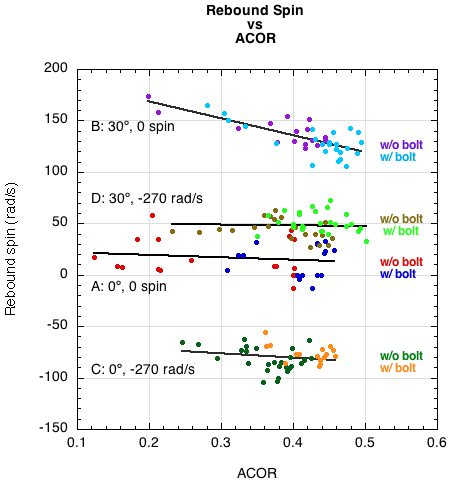
Figure 9 — Bounce spin ω₂ vs ACOR for all 165 bounces, both with and without added bolts.

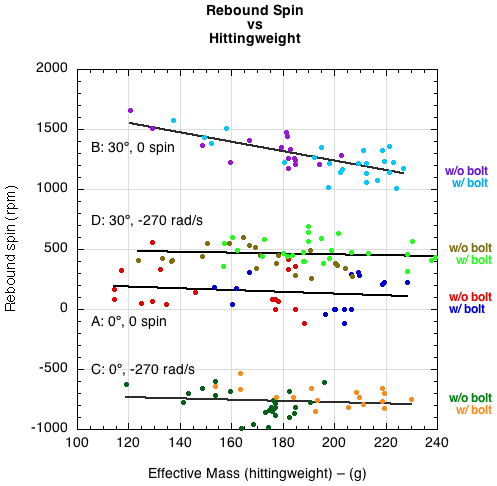
Figure 10 — Bounce spin ω₂ vs M_e for all 165 bounces, both with and without added bolts.

COEFFICIENT OF FRICTION

A surprising result is that the coefficient of friction (COF) between the ball and the strings varies over a wide range, depending on the incident ball spin and angle. The results are shown in Figure 11 (COF vs ACOR) and Figure 12 (COF vs Hittingweight). Usually, the coefficient of friction is defined as the ratio of the horizontal force to the vertical force acting on an object moving along a horizontal surface. When a ball impacts the strings, the forces perpendicular and parallel to the strings vary with time, and the ball can also slide on the strings or grip the strings. A more convenient definition of the COF in that case is COF = (change in parallel speed)/(change in perpendicular speed), which is the ratio plotted in Figures 11 and 12.

If the ball is incident at right angles to the string and bounces at right angles then the parallel speed is zero so COF = 0. If the ball is incident with backspin at an angle away from the normal, then the ball will tend to slide on the strings and the COF will be relatively large, about 0.4 in the figures. Otherwise, the ball will slide for a short time then grip the strings, in which case the COF is smaller.

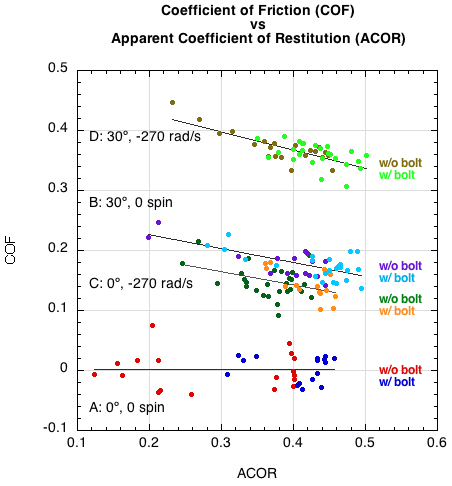
Figure 11 — Coefficient of friction COF vs ACOR for all 165 bounces, both with and without added bolts.

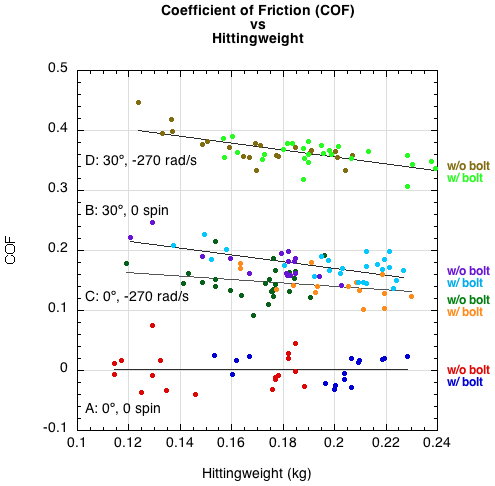
Figure 12 — Coefficient of friction COF vs M_e for all 165 bounces, both with and without added bolts.

CONTACT VELOCITY

As much as hittingweight and ACOR might influence the rebound, the incident parameters matter more. Incident speed, spin, and angle combine to determine the contact velocity tangential to the stringbed (V_c = Rω₁ + v_x1). Friction acts opposite V_c and its duration will in part depend on the magnitude of V_c. Friction acts to slow the ball and to reverse the direction of spin. The spin is changed at a faster rate than is the linear ball speed. This is shown in Figures 13 and 14. Figure 13 shows that for a given contact velocity, the rotational contact velocity component is changed a little more than 1.5 times as much as the linear contact velocity component. Figure 14 makes this clear by plotting the change in the rotational component to the change in the linear component.

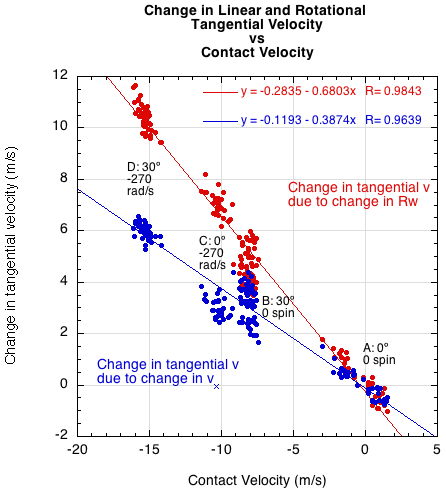
Figure 13 — Change in linear and rotational tangential velocity vs contact velocity.

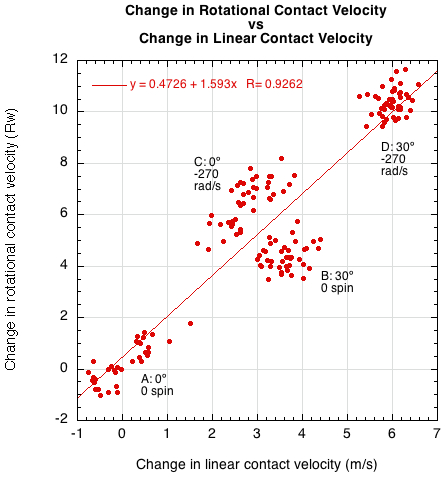
Figure 14 — Change in rotational tangential velocity vs change in linear tangential velocity.

Figure 15 shows the dependence of COF on contact velocity. The greater is V_c, the longer friction will act before the ball grips the string and the greater will be the change in linear and rotational speed. In other words, a larger V_c is associated with more sliding on the strings.

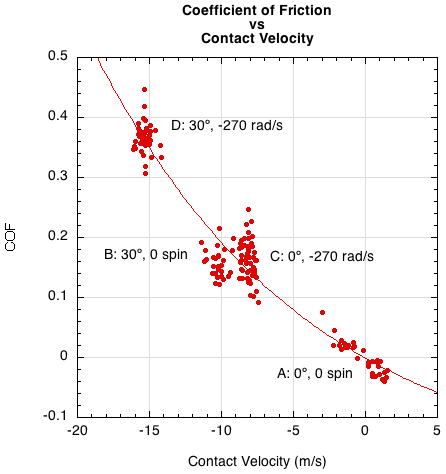
Figure 15 — Coefficient of friction (COF) vs contact velocity.

The change in rebound spin (ω₂ - ω₁) is strongly dependent on contact velocity (Figure 16). Change in spin is used instead of the actual rebound spin because it shows the direction and magnitude of work done by friction independent of the final sign of ω₂. The positive change in spin for all impacts indicates that friction acted in the topspin direction. The final bounce may have been spinning with topspin, or if it still had backspin, it would be greatly reduced.

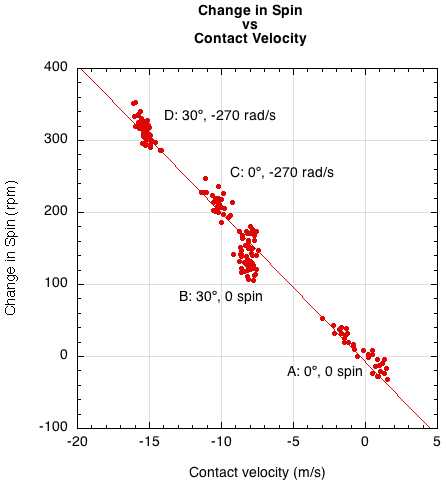
Figure 16 — Change in spin (ω₂ - ω₁) during impact vs contact velocity (V_c).

The change in rebound angle (θ₂ - θ₁) is not as dependent on contact velocity (Figure 17).

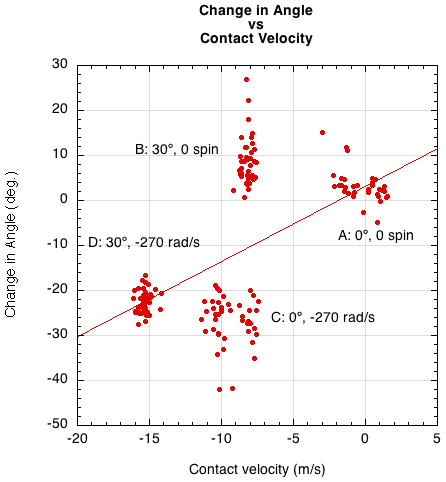
Figure 17 — Change in angle (θ₂ - θ₁) during impact vs contact velocity (V_c).

CONCLUSION

This experiment has shown that both control and power are increased by adding mass to the racquet in order to increase the hittingweight at the impact point. A higher hittingweight can be obtained by either selecting a racquet that has a high swingweight and twistweight or by customizing an existing racquet by adding lead or tungsten tape to the frame. A racquet with a high hittingweight at the impact point will twist, rotate, and translate less than a racquet with a lower hittingweight. That means a truer, faster bounce — in otherwords, more power and control.

However, the two factors that most contribute to power and control are the angle and spin of the incident ball and the swing of the player. The incoming parameters can't be changed except choosing to take the ball on the rise, descent, or top of the bounce, but the player can alter the speed and angle of swing to affect a desired outcome.