1. ABSTRACT
Does lateral string movement during impact contribute to spin? Several experiments on Tennis Warehouse University (TWU) have investigated this question (Spin and String Material, Spin and String Movement, and Spin and String Pattern, Spin and Sliding Friction, and Spin and Static Friction). The assumption of these experiments was that if lateral string movement and snap-back (torquing and spinning the ball) do enhance spin, then anything that facilitates lateral movement will also tend to increase spin. The results of these experiments added support to the lateral snap-back theory. But all but one of these experiments was performed at low impact speeds. The experiment detailed here was performed at impacts around 52 mph. Impacts were filmed to observe ball-string interaction, snap-back in action (hopefully), and/or events that suggest correlations between string movement and spin.
Preview Movie
Preview of coming attractions. Do you think this string movement caused any spin? Read on.
(Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
2. INTRODUCTION
The difference in the spin produced by different strings comes down what is called the "over-spin." Over-spin is the spin produced after the ball bites the strings and exists when the bottom of the ball (i.e., contact point with strings) is spinning faster backwards than it is moving forward due to the ball's velocity at its center of mass. To understand over-spin, first consider what happens during impact assuming no lateral movement of strings (the same events happen on a court):
Steps in Spin Production
without Lateral String Movement
- The angle of impact is determined by the speed and angle of both the ball and the racquet. For all but the most extreme topspin lobs, the resulting angle of impact is between 0 and 45 degrees from perpendicular. (Hence the angles of impact in this experiment were between 30 and 45 degrees.)
- At these angles, the ball first slides on and then bites the strings. (At greater, more oblique, angles of impact the ball slides throughout the impact and many of the following steps would not apply, and in which case the friction between the ball and string will determine the outgoing spin.)
- At the biting stage, the bottom of the ball literally comes to rest (zero velocity) on the strings. This occurs when friction both slows the speed of the center of mass of the ball across the strings and increases the spin speed (in the opposite direction) at the bottom of the ball. At the biting stage, the forward speed of the ball and the backward speed of the spin are equal and opposite at the bottom of the ball, and the ball comes to rest against the strings.
- It is friction that changes the velocity and spin of the ball. Friction occurs when two surfaces move against each other.
- Because there is no relative movement between string and ball when the ball bites (grips the strings), friction (sliding friction) stops (F=0) and there is no further change in spin while the bottom of the ball remains at rest.
- At this stage all string types will have produced the same spin (each string type reverses the incoming spin into equal amounts of topspin). No matter how rough or smooth (measured by coefficient of friction) or what shape the string, at these angles the spin produced during the sliding stage will be the same. The only difference will be whether a string bites earlier (higher COF acting for a shorter period) or later (lower COF acting for a longer period).
- Even though stuck to the strings, the ball's forward and angular (spin) momentums continue, stretching the ball forward and pressing it down into the strings at its front end. Pressure thus begins to build up in front of the stuck spot trying to push the bottom of the ball backward.
- The biting condition is maintained by static friction (friction that resists movement caused by a force pushing two surfaces parallel to each other), but soon the pressure buildup in front of the ball breaks the static friction and the ball starts sliding in the opposite direction against the strings (backward on the strings compared to the ball's forward motion as a whole).
- The friction force reverses direction: because the bottom of the ball is now moving backward relative to the strings, the strings will now exert a friction force in the opposite direction — reducing the topspin.
- The same friction reversal process can then occur in the opposite direction, again reversing the direction of friction, and once again adding to topspin.
- Acting simultaneous with the friction processes, the front edge of the ball rotates into the strings while the back edge rotates out of the strings, causing a greater perpendicular force at the front of the strings. (A similar thing happens when the brakes are applied. The front end rotates down, but the front wheels react back and push up on the front wheels, preventing the whole vehicle rotating end over end.)
- This perpendicular force at the front of the strings exerts an upward torque in the opposite direction from that created by the friction, tending to decrease topspin.
- The timing of the biting and number and magnitude of subsequent friction reversals will determine whether there is an over-spin condition or not.
- Both the sliding and static coefficients of friction will influence the duration and magnitude of each friction reversal and thus the associated change in over-spin, if any.
Both the individual steps and the entire process are very complicated. But in general, it can be said that all strings produce the same spin up to the bite stage, and after that, friction events tend to cancel each other, apart from small variances in the timing and direction of these events.
But we know from measurements of spin that there is more spin produced by a tennis racquet than can be accounted for by the above processes alone. So there must be an additional mechanism(s) that produces a topspin torque and that does not occur when bouncing from a solid surface like a court. The possibility that we have been investigating is that the mechanism is the lateral movement of strings and subsequent snap-back while the ball and strings are still in contact. It is this latter condition that has been difficult to observe, but has nevertheless been postulated because other events appear contingent on its occurance.
String movement makes the entire process even more complicated. Not only do all of the above processes still occur, but the following are also added:
Additional Steps in Spin Production Due to Lateral String Movement
- When sliding begins at impact, the ball will push on the strings and the strings will push back with an equal and opposite friction force. The magnitude of the push will depend on the coefficient of sliding friction between the ball and strings.
- The strings are held in place by the static friction between strings. If the lateral force of the ball is greater than the maximum of the static friction between strings, then the main strings will slide across the cross strings.
- If the string moves forward with the ball, then the relative speed of ball to the strings is diminished. Therefore, friction duration will be shorter because it it does not have to change the spin as much to bring it to the same speed as the ball's forward motion (which is also slowing due to friction) relative to the strings. This is a negative spin producing phenomenon.
- As the string moves, it stretches, storing energy and creating a oppositely directed elastic restoration force acting to slow the ball's forward speed and increasing its spin speed.
- As the string moves, interstring sliding friction acts against this movement, thus influencing the distance (longitudinal stretch) and how much energy will be stored (energy = force x distance).
- During the bounce, the friction force between the ball and strings and between the strings is proportional to the normal force (perpendicular force pushing ball and strings together). This force increases up to the maximum deflection of the string and then decreases until the ball leaves the strings.
- As the normal force decreases, interstring friction decreases. When the elastic force of the string is greater than the interstring friction (first static and then sliding), then the string will snap back, entirely or in part, quickly or slowly, depending on the energy stored in the string.
- The returning string will exert a torque on the ball increasing the topspin.
- The force acting between the returning string and the ball is sliding friction.
- Thus, at this stage, the coefficient of sliding friction will influence the magnitude of torque applied to the ball.
One thing that immediately pops out is that if there is no string movement, then the coefficient of friction between the ball and the string does not influence over-spin much, if any, but it does if there is string movement. In the latter case, the coefficient of friction influences how much the ball will grab and move the string and, then, how much the string will grab and spin the ball during its snap-back.
It is also apparent how convoluted the process can become. There are a lot of moving parts and forces that change magnitude and direction throughout the duration of the impact. Some factors accumulate to contribute to spin and others to diminish it. It is too complicated to keep an energy accounting at each step of the process. What concerns us is the net effect. All the separate, local events and associated forces and energies will add up to a net effect. Figure 1 (thanks to Rod Cross) shows a simplified conceptual model of the snap-back process. In the figure, the strings are simulated as a rigid surface attached to a ridged wall (the racquet) connected by a spring.
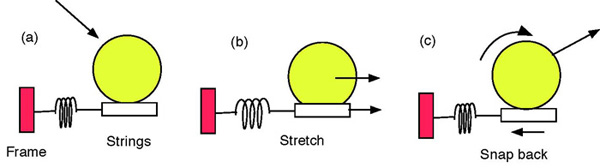
Figure 1 — The Snap-back Model of Tennis Spin. String movement as in (b) stores elastic energy in the strings, which is then given back to the ball in (c) in the form of extra spin due to the friction force at the bottom of the ball.
3. THE EXPERIMENT
As shown in Table 1, four strings in four racquets were used in the experiment.
| Table 1 Racquets and Strings | |||||
| Racquet | String | Material | Tension | Pattern | Condition |
|---|---|---|---|---|---|
| Volkl PB7 |
Babolat RPM Blast |
Polyester | 55 lbs | 16x19 | Freshly strung |
| Volkl PB10 Mid |
Klip Legend Tour (notched) |
Natural Gut | 55 lbs | 16x19 | Previously played, minor notching |
| Volkl Tour Scorcher |
Prince Synthetic Gut |
Nylon | 55 lbs | 16x18 | Freshly strung |
| Prince Original Graphite |
Polyfibre Hexablade |
Polyester | 58 lbs | 14x9 | Every other cross string skipped and strung 2 months prior |
Table 1 — Racquets and strings used in the experiment.
The closed patterns were chosen to minimize string movement. The goal was to achieve very firm but still laterally compliant surfaces such that they would sometimes produce string movement and sometimes not. If movement could be recorded and correlated with spin and if none or little movement correlated with lesser spin, we would at least have a "where there is smoke there is fire" argument supporting the lateral snap-back theory of over-spin production. This would help resolve the controversy between the two spin theories: (1) spin is maximized by a laterally immovable stringbed, and (2) spin is maximized by a laterally moving stringbed. Note, however, that we are concerned with equipment only here. If a string setup fits a particular player and allows him/her to swing faster with more control, then the result might very well be more spin. In this case, even though the equipment might be sub-optimal for spin, the net result is more spin.
The extremely open pattern was chosen to create a setup of guaranteed string movement and to compare the results to the closed patterns. Further, this racquet had lost tension after being played and then sitting a couple months. As such, after impact, the strings would tend to stay slightly out of position and the string condition might correlate to what players refer to as "dead."
Thus, these racquet/string setups present a set of varied impact conditions that, under a no lateral movement condition and associated processes noted above, would produce about the same spin. But if there is lateral movement and, additionally, differing amounts and kinds of movement, then the setups will show differing amounts of spin.
Figure 2 illustrates the experimental setup (perhaps more evident as seen in Movie Screen 2 below). A ball machine fired balls about 52 mph (nominal machine speed of 60 mph) at a stationary, freely rotating racquet. The racquet was horizontally suspended by a string attached at the head while the handle was supported by a holding device which allowed the racquet to rotate about the end of the handle upon impact. Launch angles of the ball toward the racquet were varied over a range that would encompass the angles of impact involved in very heavy topspin shots. These angles were nominally 33, 38, and 43 degrees, but because of variability in the ball launching speed, angles varied somewhat per impact. All balls were fired with a nominal backspin of about -3100 rpm, but varied slightly from one impact to the next.
A video camera was placed in two locations — (1) behind the strings in order to observe string movement (filmed at 1,000 fps) and (2) perpendicular to the oncoming ball in order to measure both incoming and outgoing spin, speed, and angle (filmed at 420 fps). The videos at each location were taken separately and no attempt was made to take simultaneous back and side videos.
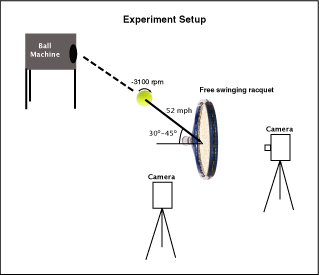
Figure 2 — Experimental Setup.
4. ANALYSIS
Movie Screen 1 shows an impact from behind each string at 32 and 42 degree angles. These videos qualitatively demonstrate the difference in string movement for each string at different angles and for the different strings at each angle. There is some indication in virtually every video of some movement, however slight. There is less movement at lower angles (i.e., closer to perpendicular) for all strings and more at higher angles (i.e., more oblique impacts). As to comparing strings, it would appear that at the lowest angle (32 degrees) the ranking of strings from low to high movement is gut, nylon, polyester, and extreme-open-pattern polyester. At the highest angle (42 degrees) the ranking is almost the same: nylon, gut, polyester, and extreme-open-pattern polyester.
Movie Screen 1.Videos of separate 52 mph impacts for the four string types at average impact angles of 32 and 42 degrees from perpendicular.
(Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
To make it easier to analyze the comparative string movements, an image was captured at maximum deflection from the lowest and highest impact angles from the videos in Movie Screen 1 above. This is displayed in Figure 3.


Figure 3 — Impacts at maximum deflection. Images are at approximately maximum perpendicular deflection of the stringbed for 52 mph impacts at an average of 32 and 42 degrees from perpendicular.
The figures show that string movement can happen in many different ways. Variation exists in the location (back, middle, front) of the ball, the number of strings that move, the distance that each moves, and when during the impact they move. And though we cannot see it in the images, presumably there is some difference in the way all of these patterns occur during snap-back. This large variance in movement configuration helps to explain the spin variance in individual strings from impact to impact at the same angle that we will examine later.
The movies in Movie Screen 1 show that it takes 2-3 frames (2-3 thousandths of a second) for the impact to reach maximum deflection. Then, because the racquet is accelerating backward, the rebound takes only 1 frame or thousandth of a second. Sometimes it might take two, but it is difficult to observe. In that 1/1000 second, somewhere in the time from one frame to the next, the ball rebounds and the strings (for the most part) snap back. If this snap-back occurs while the ball is still on the strings, as we infer it must, then the snap-back will increase spin. (Note: Especially with the 14M x 9X Hexablade poly racquet, it is tempting to say that there is visual evidence for snap-back while the ball is compressed against the strings. However, many times what looks like a string snapping back is an illusion caused by the one in front of it moving forward even more.)
Given this qualitative assessment of string movement, the next step is to measure the inbound and outbound spin, speed, and angles, with a goal of comparing the spin at each angle with the qualitative judgement of string movement at each angle. Movie Screen 2 displays one example of the impact and rebound for each string at each angle.
Movie Screen 2.Videos from the side for 52 mph impacts at average angles of 32, 37, and 42 degrees from perpendicular.
(Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
Using the data obtained from these videos, Table 2 displays the average values of input and output parameters at each angle (use the left/right scrollbar to see all the data).


| Racquet | String | Material | Pattern (MxX) | Incident Angle (deg) | Incident Velocity (m/s) | Incident Spin (rpm) | ACOR (ea) | eT | Rebound Angle (deg) | Rebound Spin (rpm) |
|---|---|---|---|---|---|---|---|---|---|---|
| Volkl PB7 | Babolat RPM Blast | Polyester | 16x19 | 32.2 | 22.93 | -3057 | 0.399 | 0.015 | 24.2 | 1098 |
| Volkl PB7 | Babolat RPM Blast | Polyester | 16x19 | 37.6 | 23.17 | -3255 | 0.433 | 0.032 | 25.8 | 1351 |
| Volkl PB7 | Babolat RPM Blast | Polyester | 16x19 | 41.5 | 22.87 | -3233 | 0.436 | 0.044 | 31.8 | 1675 |
| Volkl PB10 Mid | Klip Legend Tour (notched) | Natural Gut | 16x19 | 32.5 | 22.93 | -3113 | 0.379 | -0.009 | 26.3 | 983 |
| Volkl PB10 Mid | Klip Legend Tour (notched) | Natural Gut | 16x19 | 36.9 | 22.66 | -3168 | 0.384 | 0.021 | 30.3 | 1324 |
| Volkl PB10 Mid | Klip Legend Tour (notched) | Natural Gut | 16x19 | 42.5 | 23.58 | -3136 | 0..405 | 0.015 | 37.6 | 1680 |
| Volkl Tour Scorcher | Prince Synthetic Gut | Synthetic Gut | 16x18 | 30.4 | 22.51 | -3048 | 0.353 | 0.03 | 20.6 | 938 |
| Volkl Tour Scorcher | Prince Synthetic Gut | Synthetic Gut | 16x18 | 36.6 | 23.36 | -3152 | 0.401 | 0.014 | 27.6 | 1241 |
| Volkl Tour Scorcher | Prince Synthetic Gut | Synthetic Gut | 16x18 | 41.8 | 23.09 | -3064 | 0.396 | 0.014 | 35.6 | 1557 |
| Prince Original Graphite | Polyfibre Hexablade | Polyester | 14x9 | 31.4 | 22.84 | -3054 | 0.43 | 0.155 | 6.2 | 1276 |
| Prince Original Graphite | Polyfibre Hexablade | Polyester | 14x9 | 38.7 | 23.43 | -3143 | 0.452 | 0.159 | 11.0 | 1628 |
| Prince Original Graphite | Polyfibre Hexablade | Polyester | 14x9 | 42.9 | 23.2 | -3101 | 0.417 | 0.129 | 21.7 | 1810 |
In the table, ACOR (ea) is the apparent coefficient of restitution, eT is the apparent tangential coefficient of restitution:

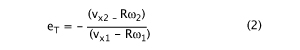
Where,
- ω1 — The angular velocity (spin) of the incident ball (radians/sec).
- ω2 — The angular velocity of the rebounding ball (radians/sec).
- vy1 — Component of incident velocity perpendicular to stringbed (m/s).
- vy2 — Component of rebound velocity perpendicular to stringbed (m/s).
- vx1 — Component of incident velocity parallel to stringbed (m/s).
- vx2 — Component of rebound velocity parallel to stringbed (m/s).
- R — Radius of ball = .033 m.
eA is a ratio of the rebound speed to the incident speed perpendicular to the stringbed and eT is a ratio of the tangential rebound speed at the contact point of the ball and strings to its incident tangential speed. eA can range from 0-1.0, but for an impact in the middle of the strings of a hand-held racquet, eA is typically about 0.4-0.5. eT can vary from -1.0 to 1.0 but is typically about 0.01 for a hand-held racquet.
The results are similar but lower (due to the non-clamped vs clamped racquet setups) than the tests reported in Spin and String Movement and Spin and Material:
- 32 Degrees: Not including the wide open pattern, the poly had 17% more spin than the nylon, with gut in the middle. Including the open pattern, the difference was 36%.
- 37 Degrees: Not including the wide open pattern, the poly had 9% more spin than the nylon, with gut in the middle. Including the open pattern, the difference was 31%.
- 42 Degrees: Not including the wide open pattern, the poly and the gut had 8% more spin than the nylon. Including the open pattern, the difference was 16%.
These results can be viewed graphically as in Figure 4. If we accept the premise that more string movement is associated with more spin, then, in general, these graphs indicate that more string movement is correlated with more spin (more over-spin), higher rebound angle (closer to perpendicular), greater tangential energy return, and slower tangential ball velocity.
The two bottom graphs are graphs of so-called 'spin parameters'. The first, Rω2 / vx2 vs incident angle is a ratio indicating the amount of over-spin. The Rω2 is the speed of the spin at the contact point of the ball and the vx2 is the linear speed of the ball. If the spin speed is more than the linear speed, then an over-spin mechanism has been at work. The second spin parameter graph — Rω1 / vx1 — is a way of taking into account the fact that rebound spin depends on both the inbound spin and velocity. The greater the inbound spin the less the outbound spin.
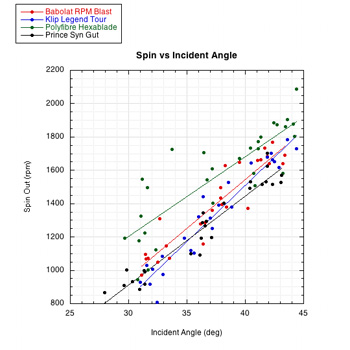
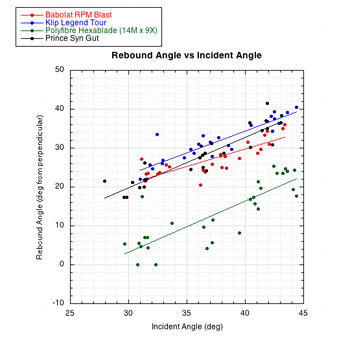
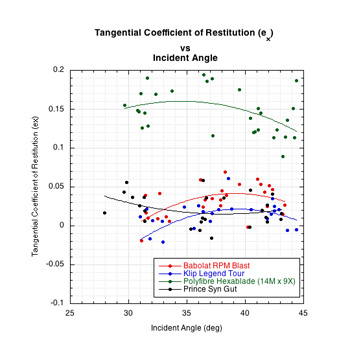
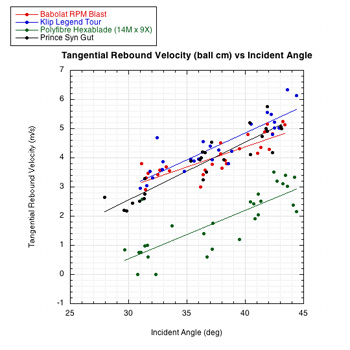
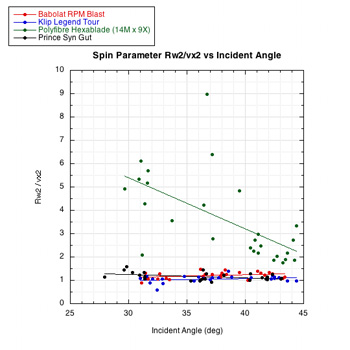
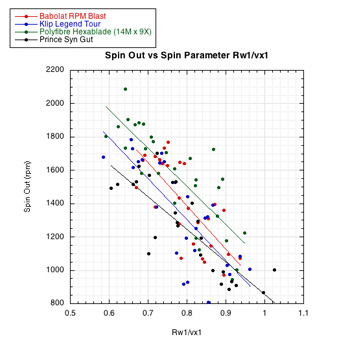
Figure 4 — Graphical presentation of impact results.
5. CONCLUSION
The videos (here and at the links above) show that string movement does indeed occur at the angles and speeds tested. It is also shown that the strings do snap back for all setups and they do so, for the most part, in less than 1/1000 second. We can't see the details of what occurs during that 1/1000 second between video frames, but the evidence makes it reasonable to assume that the strings are indeed spinning the ball. Furthermore, even when there is no visible movement, the strings can still stretch laterally between string intersections and snap-back to produce over-spin. The end result is that string movement and snap-back very strongly correlate with more spin.
These tests were performed at 52 mph. Previous tests (especially Spin and String Pattern) were performed at 7-13 mph. The greater speed produced more string-ball interaction and more string movement. However, the results were the same: setups that displayed more string movement displayed more spin.
What is also apparent by looking at the data points on the graphs is that there is a great deal of variability between impacts for any string at any angle. Judging from the multitude of movement configurations in Figure 3, the results for a given impact may depend on just how the ball lands and catches the strings. This is especially apparent with the open pattern.
What is further apparent is that the results of three previous experiments are qualitatively similar: polyester in general moves more than nylon or gut and produces more spin. That does not mean that individual strings of a particular material cannot perform much better than the average for that material. However, because spin performance does seem (at least at present) to correlate to material, the question is what is it about the string/material that makes it move and stretch laterally? The candidates from TWU string properties testing would suggest stiffness, tension loss, and slipperiness as the main candidates. Polyester is stiffer, loses more tension, and is slippery. The stiffer material may be more able to overcome interstring friction or move faster, the lower tension decreases interstring friction enabling more movement, and slipperiness (low coefficient of friction — COF) also lessens interstring friction. These may all act in interactive combinations to facilitate string movement and snap-back. The precise mechanisms of snap-back are yet to be determined.
But it must be remembered that just because a particular string has better spin properties, that does not mean that the player will be able to hit more spin with it. The main contributors to spin, over and above the equipment, are the speed and angle of the swing. If the equipment setup causes the player, for control, strategic, or confidence reasons, to alter the swing, then there may be a decrease in spin. Alternatively, the player might speed up the swing or increase the attack angle or racquet tilt and get even more spin. That, probably, is the reason that lab tests and playtests don't always agree for everyone.

