INTRODUCTION

Experiments analyzing racquet performance during collisions with tennis balls use several methods to secure the racquet — free-standing, hand-held, head-clamped, and handle-clamped. The concern is that the securing method can alter performance. Each method allows or prevents certain degrees of freedom of movement. A free racquet will translate, rotate, twist, bend, and vibrate. Any other method to hold a racquet in place may alter one or more of these degrees of freedom from what one might expect or measure during an actual tennis shot. A head-clamped racquet does not allow any movement and therefore is not considered an accurate reflection of on-court reality. A handle-clamped racquet prevents translation and rotation and alters the bending modes, vibration frequencies, and hence also usually disqualified as a realistic predictor of performance. The two remaining methods are free-standing and hand-held. The main question is that, although a hand-held racquet allows all degrees of freedom of motion, it may alter the magnitude of these motions and thus the performance of the racquet. The theoretical consensus is that the ball leaves the strings before it receives any information from the handle on whether it is hand-held or free. We test that here.

EXPERIMENT

Balls were fired perpendicular to the racquet face at 15 m/s with no spin. The racquet was either free-standing (balanced) or hand-held horizontally to the incoming ball (Figure 1). Balls were aimed to vary from tip to throat on the long x-axis and only those that hit within ± 1.6 cm were chosen. A camera was positioned behind the racquet to capture the impact coordinates. A camera positioned to the side parallel to the incoming ball captured the incident and rebound velocities.

Figure 1 — Experimental setup for impacts with a free-standing racquet (left or top) and a hand-held racquet (right or bottom).

RESULTS

When the ball hits the racquet, local bending occurs. The racquet does not then immediately traslate or rotate because the center of mass and axis location do not yet "know" that an impact has taken place. It takes time for the information to travel. The information of the occurrence of impact travels on the transverse bending wave — i.e., each point on the racquet pulls on the point on either side of it and the local bend propagates up and down the racquet to the tip, CM, and handle. The speed of this wave depends on the local stiffness and mass along its travels. Stiff sections vibrate faster and heavy sections vibrate slower. Heavy sections also translate and rotate more slowly. Most racquets vibrate around 150 Hz. That is one cycle (period) about every 7 ms. That is how long it takes the wave to make one full found trip from one end of the racquet to the other and back again. This period is the net result of the wave bending its way across all the local stiffness and mass variations along the racquet.

If the ball hits 4 inches from the tip, then it will take about 6 ms to make the round trip to the handle and back, but the ball leaves in 4-5 ms. So the ball never gets the information (energy) about how stiff the racquet is nor how much it translates at the center of mass or rotates about the axis at the wrist. If, on the other hand, the ball strikes near the throat about 19 inches from the butt, the wave will get back to the ball in about 4.9 ms. This is just as the ball is leaving but may still give it a little boost. So, in theory, impacts at the tip should be unaffected by what is going on at the handle and impacts near the throat might be. For throat impacts then, the hand would act to add mass and limit both translation and rotation, thus saving energy that could go back into the ball if the bending wave gets back in time. So what did we find?

The performance parameter measured was the apparent coefficient of restitution (ACOR). ACOR is defined as the ratio of the rebound speed perpendicular to the stringbed (v_x2) to the incident perpendicular speed (v_x1) (Equation 1):

      (1)    ACOR = e_A = v_x2 / v_x1

where e_A is the symbol for ACOR used in formulas. ACOR is usually about 0.5 in the center of the throat area, 0.4 in the center of the stringbed and about 0.1-0.2 at the tip and on the periphery. Figure 2 shows the ACOR results vs the distance of impact from the tip.

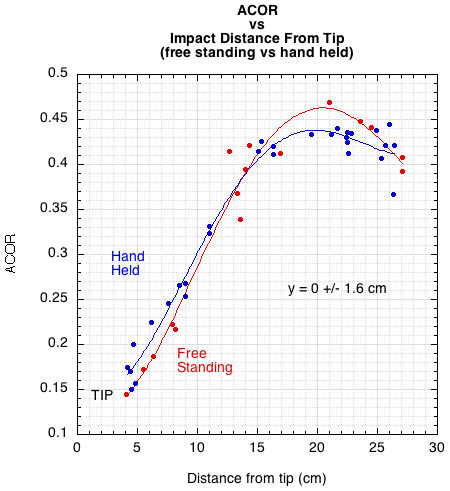
Figure 2 — ACOR vs distance from tip for both free-standing and hand-held conditions.

The curve fits for each support condition are very similar. However, there is a bit of separation at the bottom and the top of the curves. The separation is opposite to what might be expected. At the tip, no separation is expected, and at the throat, if there were any at all, it would be expected that the hand-held racquet would have a higher ACOR since it would translate and rotate less. There is one impact point in the throat for the free-standing curve that may, perhaps, cause this unexpected separation. That being the case, perhaps combining all the data points into one curve is a more realistic option (Figure 3).

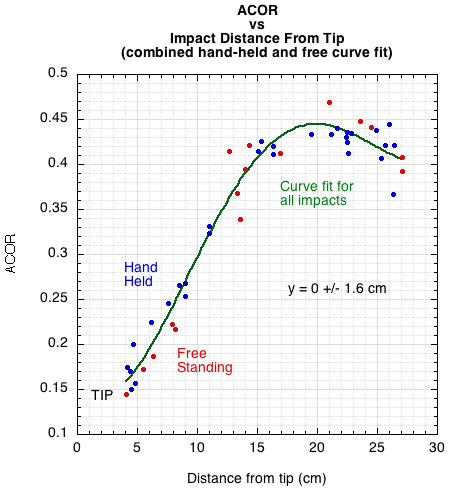
Figure 3 — Combined curve fit for ACOR vs distance from tip for both free-standing and hand-held conditions.

CONCLUSION

The generalized conclusion is that there is essentially no difference in ACOR between the free-standing and hand-held conditions. A bit of skewing distorts the picture and a data set with many more impacts would be helpful in determining if there is any statistically significant separation of curves or not.