INTRODUCTION

Tennis players maintain that changes in either the string tension or material can make large differences in ball speed and its associated "feel." Shot speed is measurable, but "feel" is a subjective interpretation derived from measurable (and perceptible) events such as force, shock, vibration, deformation, contact time, sound, and stiffness. These interpretations then may influence players' perceptions of what they think the ball speed is. Those interpretations are often then connected to the racquet or string as a "property" such as "soft," "powerful," "harsh," "solid," "tinny," etc. Often the interpretation is contrary to the measurement, especially with regards to ball speed. The findings of this experiment show that string tension and material have only a small effect on ball speed, even while having a more significant affect on the feel parameters, at least at lower tensions.

This experiment traces the flow of energy during an impact between a tennis ball and stringbed, examining the differences in energy flow between different string materials and tensions. Instrumenting and measuring the instantaneous force, deformation, stiffness, and energy of the ball and strings is difficult given the dynamic context of such an impact. This experiment eliminates these difficulties by simulating a ball-racquet impact in a semi-dynamic manner in the lab. The usual impact between a ball and racquet is one-sided, with the force acting at the surface between ball and stringbed. The ball is compressed at the stringbed surface, but as the front of the ball is brought to a stop, the back of the ball continues forward compressing the ball at the top also. The force is one-sided but the ball deformation is two-sided.

This experiment achieves the same two-sided ball deformation, but it does so by also making the force two-sided. This is done by dropping a mass onto a ball resting on the stringbed (a similar procedure was performed by Y. Kawazoe in 2002 [1]). As such, the force on the ball is two-sided and that on the strings is one-sided. This procedural technique does not alter the energy result as compared to a normal ball-racquet collision. The energy flow, storage, and return behave the same whether the force is one or two-sided. For calculations, the two-sided ball interaction is resolved into two separate one-sided interactions — the force of the strings on the ball on one side and the force of the mass on the ball on the other side.

This procedure allows the tracking of energy from the dropped mass to the strings and ball and back to the rebounding mass. The energy return to the rebounding mass is the same as would be that of a rebounding ball from a stringbed. The reason is that the drop weight is relatively heavy and slow compared to a high speed colliding ball, but it compresses the ball the same amount, so the force on the strings is about the same. The only relevant difference is that the impact force lasts longer. That is because it takes longer to reverse the momentum of the heavier mass. The duration of the drop mass impact is 35-60 ms on strings, 60-65 ms on the ball, and 70-85 ms on the string-ball combination. For a normal ball and racquet collision the duration is about 5 ms. The longer time may decrease the energy return of the ball 1-2 percent but does not noticeably affect the stringbed energy return.

The relative stiffnesses of the ball and stringbed determines the energy flow and storage between them, and the energy return property (coefficient of restitution, or COR) of each determines how much is given back. Stiffness and COR were determined by separate impacts on the stringbed alone and the ball alone. These properties could then by used to predict the energy return of the drop mass rebounding from the ball-stringbed combination.

EXPERIMENT

An impact device was built such that a mass could be dropped from a height onto an object. Both the mass and the drop height could be varied. For this experiment the mass was 4.77 kg (10.5 lb) and the height 175 mm (6.9 in). The impact velocity of the mass was 1.82 m/s (4.1 mph) and the impact energy was about 8 J. The mass was dropped separately onto a stringbed, a ball, and a ball resting on a stringbed. The mass and height created an average impact force comparable to that of a 50-60 mph serve. Movie Screens 1, 2, and 3 show these three impact scenerios.

A Babolat Pure Strike (98 square inches and a 16x19 string pattern) was used for all experiments and was clamped in place to control for all racquet variables except string type and tension. Two strings were tested, one nylon (Tecnifibre NRG2 16) and one polyester (Babolat RPM Blast 16). These strings were chosen because they represent the most commonly used string materials and because one is soft (nylon) and the other stiff (polyester). Racquet tensions were 15, 25, 35, 45, 55, and 65 pounds. All impacts were in the middle of the stringbed.

Depending on the test type, the ball was secured either to the bench top or the stringbed with double-sided tape. After every impact, the ball was rotated to a perpendicular axis for the next hit.

The drop mass was equipped with a force gauge and an LVDT to capture impact force and deformation.

RESULTS

Ball speed is a direct result of energy flow — i.e., where and how much energy is stored in the strings and ball and how much is returned from each. The relative stiffness of materials determines the "how much" and "where" of storage, and the coefficient of restitution (COR, or e) measures how much of that energy is returned. In a typical ball-racquet collision, COR is a ratio of the rebounding ball speed (v₂) to the impact speed (v₁). Expressed instead as energy return, it is equal to COR squared (e²). In this experiment, COR is measured a bit differently. Here COR is the ratio of the rebounding speed of the drop mass to its impact speed. However, even though the energy loading mechanism is different from a typical ball-racquet collision, the impact energy is stored and returned in the same way.

Measurements of COR were taken in two ways. First the COR of each stringbed and ball was measured by dropping the mass separately on the clamped stringbed and on the ball taped to the tabletop with double sided tape. In that way, all the energy of the impact mass was converted into elastic energy in string or ball deformation. The second COR measurement was calculated from the mass dropping on the combination of the ball resting on the stringbed. The two results are displayed in Figure 1.

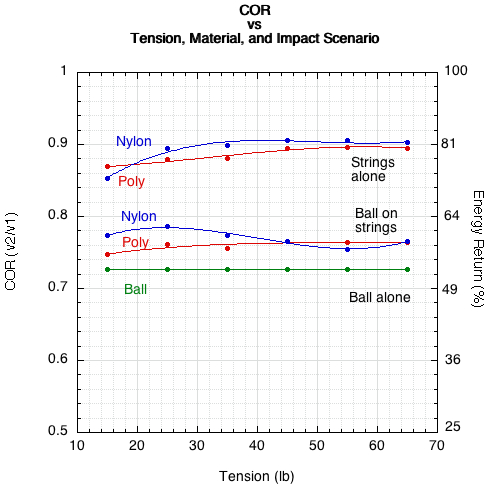
Figure 1 — Average coefficient of restitution by string tension and impact scenario: impacts on polyester and nylon stringbeds, impacts with ball resting on each stringbed, and impact with ball alone on tabletop. The right axis is energy return = COR² x 100.

Figure 1 shows that the stringbed has the highest COR (or energy return percent) and the ball the lowest. The combined ball-stringbed COR is in-between. Contrary to expectation, the COR of the stringbed alone decreased slightly at lower tensions for both polyester and nylon. And for the combined ball-stringbed impacts, it increased for nylon and decreased for polyester. The nylon ball-on-strings curve is what is generally expected for both scenarios. However, in general, there is not a great deal of difference in COR between string materials or tensions. At most there is a difference of about 0.02-0.03. Further, the greatest differences for the ball-stringbed impacts occur at tensions below 45 lb that are rarely used by players. Where is the disconnect between perception, interpretation, and performance? We have to track the energy flow from drop mass to strings to ball and back to drop mass to explore further.

Energy flow depends on the relative stiffness of the materials. If we know the ball and stringbed stiffnesses and the COR of each, we can predict the COR for the combined ball-stringbed impact. Therefore, the stiffness of the ball and stringbed must first be measured independent of each other. Further, the mass used to apply the test force must itself be essentially non-deformable so that all deformation will occur in the material of concern. A steel impact head directs all the energy and deformation into the stringbed or the ball. Because string material and tension are both input parameters, we have to measure stiffness of each material at each tension. The input parameters for the ball-alone impact do not change, so the stiffness of the ball is constant.

Figure 2 shows the technique and geometry of deformation for the three impact scenarios — ball alone, stringbed alone, ball resting on stringbed. The ball is squeezed between the drop mass and the stringbed. It is assumed that the force and deformation at each surface will be the same.

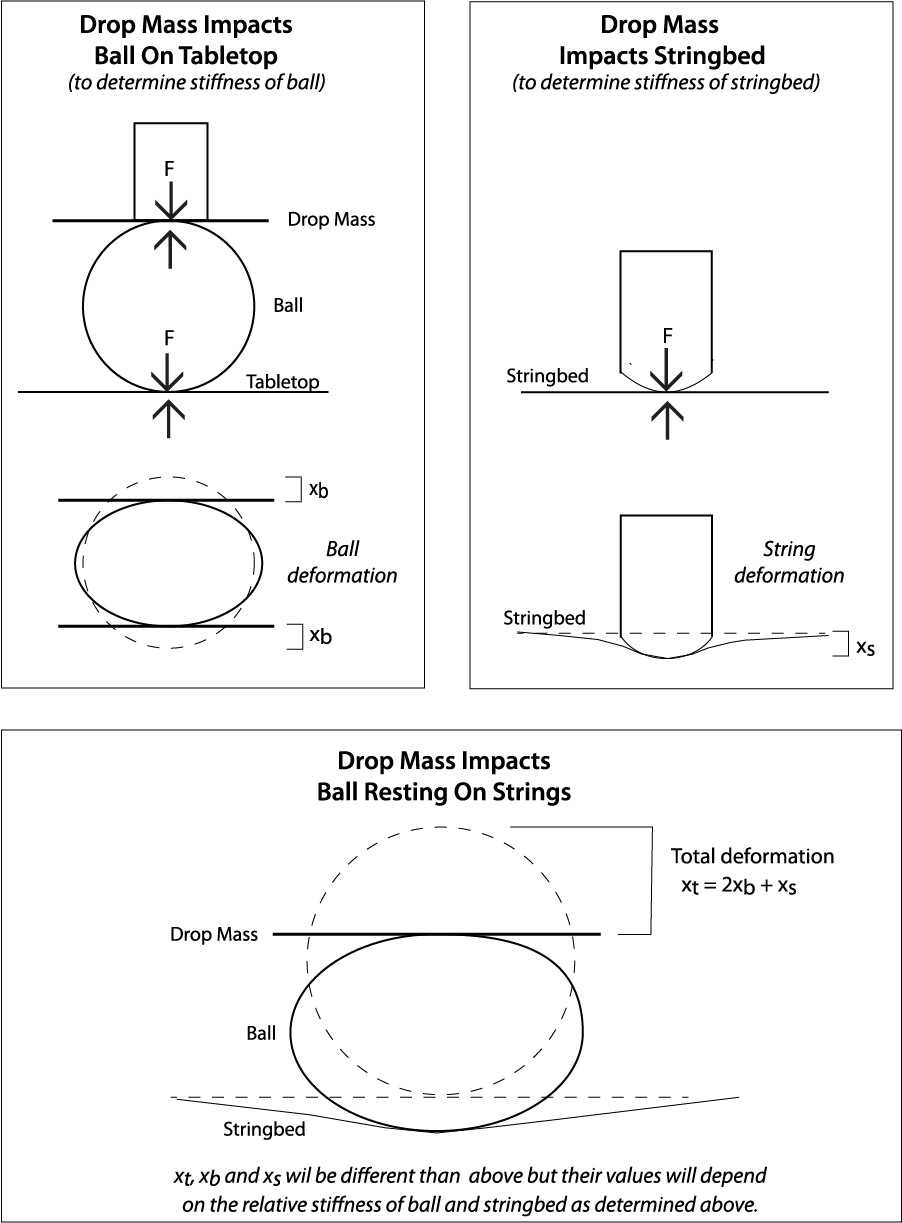
Figure 2 — Deformation of ball and string when impacted by the drop mass.

Stiffness is given by

(1)

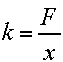
where k is stiffness, F the force, and x the deformation. A subscript is attached to each: "s" for strings (e.g., k_s), "b" for ball (e.g., x_b), and "t" for total (e.g., x_t). The stiffness of the ball-only test was doubled to be equivalent to a one-sided test. In that way, all deformations at each ball or string interface were then calculated using one-sided values. Figure 3 shows the stringbed and ball stiffness properties.

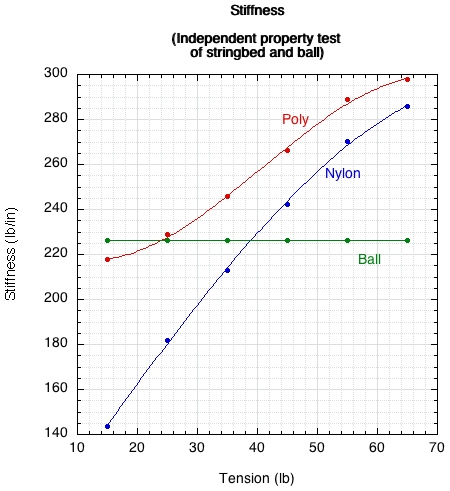
Figure 3 — Average stiffness by string tension and material for stringbed only (both polyester and nylon) and ball only tests.

It is apparent that polyester is significantly stiffer than nylon at all tensions, and both stringbeds are stiffer than the ball above tensions of 40 lb. Nylon is significantly softer than the ball below 45 lb tension. If we know the relative stiffness of the stringbed to the ball, we should be able to predict the deformations, energy storage, and energy return of each ball-string combination at different tensions. We know that the force on the stringbed equals that on the bottom of the ball and that equals the force at the top of the ball. So, by Eq. 1, we see that

(2)

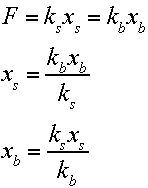
where k_s is string stiffness, x_s is string deformation, k_b is ball stiffness, and x_b is ball deformation on one side only. The ratios of stringbed deformation to total deformation and of ball deformation to total deformation can now be calculated. First, stringbed deformation to total deformation is derived:

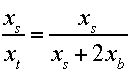
Substituting k_bx_b/k_s for x_s and doing some algebra, we end up with

(3)

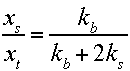
Similarly, total ball deformation (x_bt) to total deformation becomes

(4)

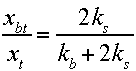
To calculate the ratio of stringbed energy to total stored elastic energy, we proceed as follows. Energy is given by

(5)

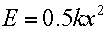
where E is energy, k is stiffness, and x is deformation. So, the energy fraction in strings to the total impact energy (E_s to E_t) is

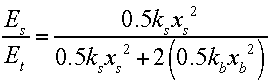
The numerator is the energy stored in the strings and the denominator is the total stored energy which equals the stringbed energy plus the energy stored in each side of the ball. Substituting k_sx_s/k_b for x_b and applying some algebra, we get the energy fraction stored in the stringbed:

(6)

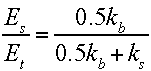
Similarly, by substituting k_bx_b/k_s for x_s, we get the ratio of energy stored in the ball compared to the total impact energy:

(7)

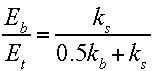
As shown in Figure 1, we know the energy return of the ball and stringbeds at each tension and we know the energy of the drop mass at impact. If we multiply the energy return of each stringbed at each tension by the energy storage fraction for each stringbed at each tension (Eq. 6) we get the energy return fraction for the stringbed. If we do the same for the ball (using Eq. 7), we get the energy return fraction for the ball. Added together we get the total predicted return fraction of the initial energy. Figures 4 and 5 show the predicted to the actual energy return for each stringbed.

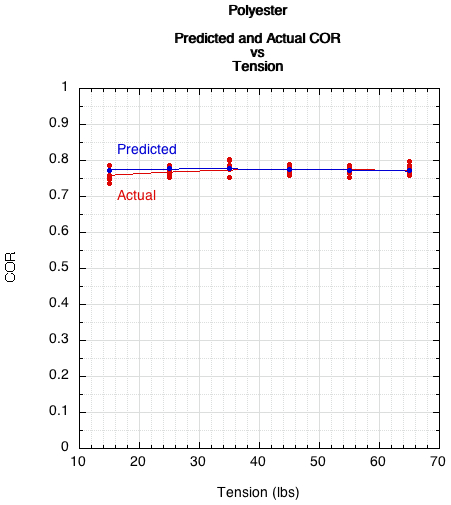
Figure 4 — Predicted and actual COR for polyester stringbed.

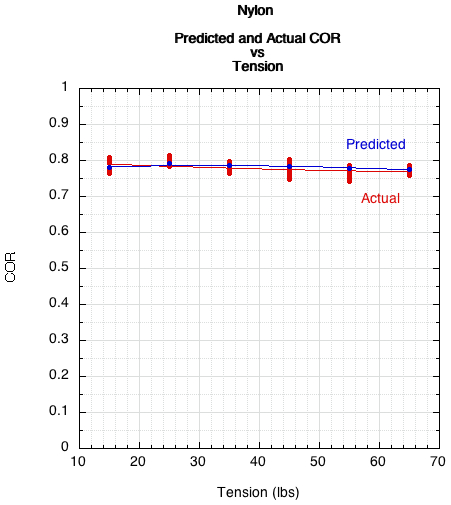
Figure 5 — Predicted and actual COR for nylon stringbed.

The predicted and actual are practically equal, and both indicate that there is little change in COR for either material as stringbed tension is changed. For both strings, as tension decreases, the share of energy storage increases for the stringbed and decreases for the ball. That is because the relative stiffness of the stringbed to the ball decreases. For polyester, the energy return declines enough to offset the increase in storage in the stringbed as opposed to in the less efficient ball. The same occurs in nylon, but only at the very lowest tension. This is displayed for polyester in Figure 6 and for nylon in Figure 7.

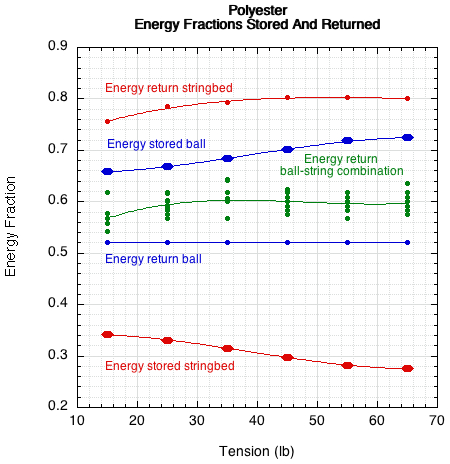
Figure 6 — Energy fraction breakdown for polyester. The average energy return for the ball-stringbed combination is the result of energy returned by stringbed times energy stored stringbed plus energy returned ball times energy stored ball.

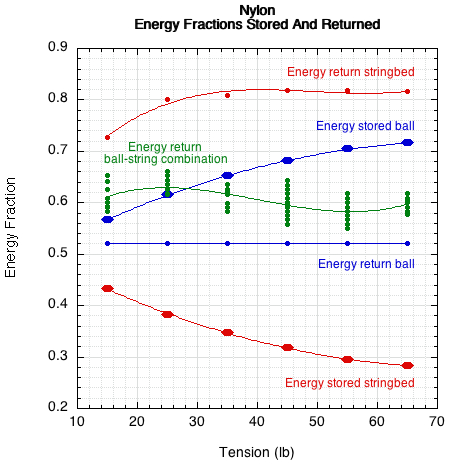
Figure 7 — Energy fraction breakdown for nylon. The average energy return for the ball-stringbed combination is the result of energy returned by stringbed times energy stored stringbed plus energy returned ball times energy stored ball.

The above discussion explains why COR and energy return vary so little between materials and tensions. But why do players believe they vary a great deal? The results below indicate that the contemporaneous "feel" events associated with power production do vary by significant and, perhaps, perceptible amounts and could contribute to such beliefs. Figures 8, 9, and 10 show polyester vs nylon for force, deformation, and impact duration.

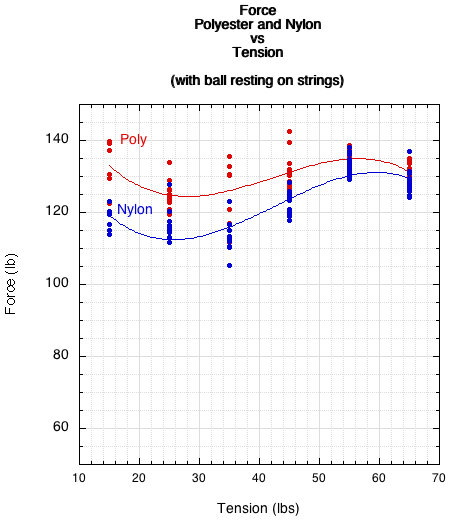
Figure 8 — Force: polyester vs nylon vs tension.

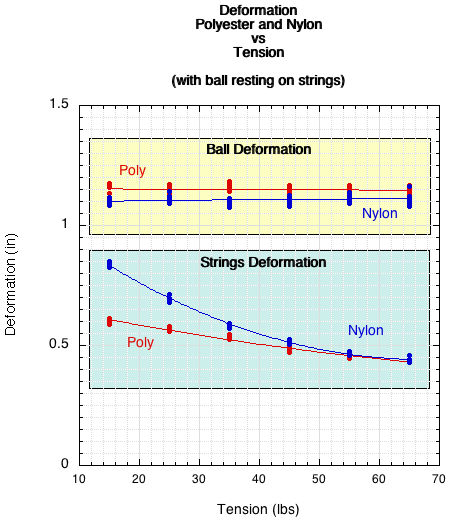
Figure 9 — Deformation: polyester vs nylon vs tension.

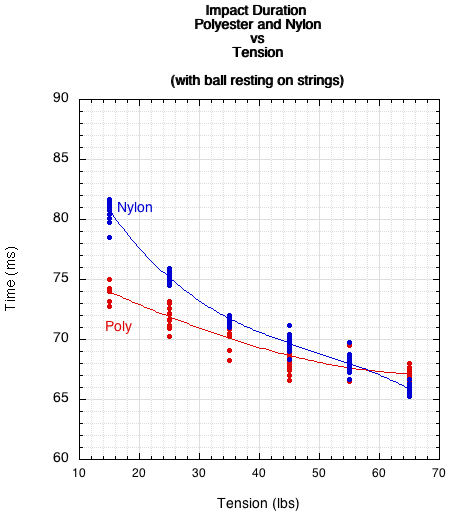
Figure 10 — Impact duration: polyester vs nylon vs tension.

If we calculate the percent difference of nylon compared to polyester for each parameter at each tension, it is easier to compare relative differences and to determine whether a player might perceive the difference. Figure 11 shows this result.

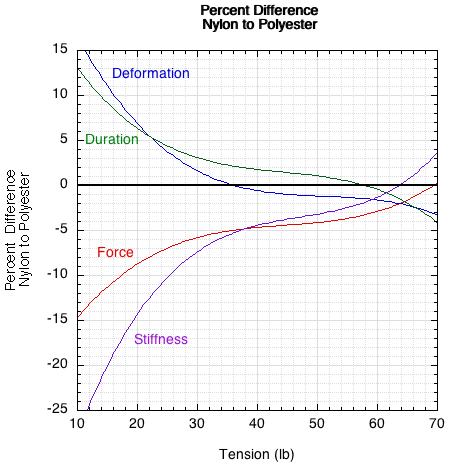
Figure 11 — Percent difference of nylon to polyester for force, deformation, duration, and stiffness.

It is clear from Figure 11 that above 35 lb tension there is little (less than 5%) difference between material or tension in any of the four parameters. Below 35 lb the difference between materials increases — probably enough to perceived (although few if any players string racquets below 35 lb). To know for sure, experiments would have to be done on player sensitivity to changes in each of these parameters.

CONCLUSION

If we know the COR and stringbed stiffness at any given tension and the ball COR and stiffness, we can predict the COR of an impact between the two. Both the prediction and the actual measurement indicate that there is not much variation in COR between materials or tensions. There is a bit of variation at tensions below 35 lb, but few players string their racquets at those tensions. There may be a "feel" difference however. The same value of COR can be obtained by a large force for a short time or by a small force for a longer time. If the player can perceive such differences, then they may attach meanings to them. So, the same ball speed result might be thought of as "powerful" to one player and "dead" to another based on the feel and its associated interpretation.

In general, if more energy can be stored in the strings, it is usually thought that there will be more energy return. Energy is directed into the strings by decreasing the stiffness of the stringbed. This is done by decreasing tension or changing to a less stiff material. However, if either change lowers the COR of the string at the desired tension, then the result of more energy going into the string may be cancelled by the lower energy return.

References

Kawazoe, K. (2002) Dynamics of the Ball-Racket Impact in Tennis: Contact Force, Contact Time, Coefficient of Restitution, and Deformation. Proceeding of ACMD 2002, The First Asian Conference on Multibody Dynamics 2002, 286-293.