INTRODUCTION

The speed of a tennis ball off the strings of a racquet depends on the speed of the racquet. It also depends on the impact point on the strings and it depends on the mass of the racquet head. String tension also plays a small role, but it is much less important than the other three factors. A racquet with a very light head can be swung faster than one with a very heavy head, but neither of these racquets would be particularly useful since a very light head would pack very little punch and a very heavy head would make the racquet too sluggish. For that reason, all tennis racquets weigh about 300 grams, with roughly half the weight in the head and half in the handle. In that respect, all tennis racquets are about equally powerful, although some are slightly more powerful than others.

Figure 1 — Collision of mass M with a ball at rest.

Colliding Balls

The impact of a racquet with a ball is similar to the collision of one ball with another. Suppose that a ball of mass M and speed V collides head-on with a stationary ball of mass m, as shown in Fig. 1. That is equivalent to a serve in tennis with a racquet of mass M and a ball of mass m. If the collision is perfectly elastic so that there is no loss of energy during the collision, then the speed of the initially stationary ball after the collision is given by

(1)       v = 2MV / (M + m)

That equation indicates that if we want to increase v then we need to increase M or V and we need to decrease m. In tennis we can't decrease m so the only options are to increase M or V or both. Increasing M helps up to a point but if M is much larger than m then any further increase in M will make very little difference. If M is much larger than m then equation (1) reduces to v = 2MV//M = 2V, which is the maximum possible value of v if there is no loss of energy. If M is equal to m then v = V, which is the standard result for the collision of a billiard ball with another billiard ball at rest.

There is another problem if we try to increase M. If the mass of the racquet is large then it can't be swung very fast so V will be small, and if M is small then the racquet can be swung at high speed but it can't be swung faster than the arm alone. So, what is the best value of M to maximise the speed of the ball? Some years ago I conducted an experiment to measure the throw speed of several different balls of different mass. I could throw a 45 g golf ball at about 25 m/s and I could throw a 3 kg ball at 10 m/s, so there was not a huge difference in throw speed, despite the huge difference in ball mass. The reason was that I could apply a much bigger force on the heavy ball. If I were to throw a piece of paper, then the force on the paper would be tiny. The force on a mass m in the hand is given by F = ma where a is the acceleration of the hand, which depends on the mass of the hand and arm plus the muscle forces applied to the arm.

Suppose that in Fig. 1 the incident ball is thrown at the stationary ball so that the incident ball speed varies with its mass according to the relation

(2)       V = 13.2 / M^1/4

where V is the speed in m/s and M is the mass of the ball in kg. Equation (2) is not a theoretical result. Rather, it was found to give a good fit to the measured throw speeds when M was varied. For example, if M = 3 kg then V = 10 m/s and if M = 0.045 kg then V = 28 m/s. If m = 57 g (the same as a tennis ball) then the incident and outgoing ball speeds would vary as shown in Fig. 2. In that case, maximum outgoing speed occurs if M is about 0.15 kg, which implies that the mass of a tennis racquet head should be about 150 g to achieve maximum serve speed.

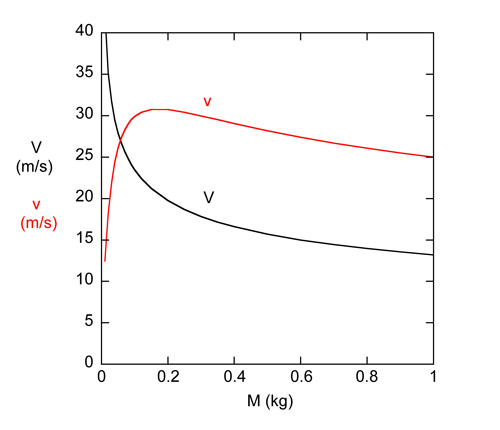
Figure 2 — Incident ball speed, V , and outgoing ball speed, v.

Racquet Speed

A similar relation exists between the swing speed of a tennis racquet and the mass of the tennis racquet, with one notable exception. That is, the swing speed of a racquet depends on its swingweight rather the actual weight of the racquet. If most of the weight of the racquet was in the head then it would be more difficult to swing than a racquet with most of its weight in the handle, even if both racquets had the same total weight. A racquet with a swingweight SW = 100 kg.cm² can be swung at a speed of about 54 m/s (194 km/hr) while a racquet with a swingweight SW= 400 kg.cm² can be swung at about 38 m/s (137 km/hr) depending on the strength of the player. In that case, the speed of the racquet at the mid point of the strings is given approximately by

(3)       V = 170 / SW ^1/4

Then V = 53.7 m/s if SW = 100, and V = 38.0 m/s if SW = 400. The speed at the racquet tip will be larger than this, and the speed in the throat region will be smaller. Equation (3) is not an exact formula. For example, the number 170 will vary with the strength of the player and the 1/4 power might be 0.23 or 0.27 for some players, depending on their swingstyle. Equation (3) can be used as a typical result to show how racquet power varies from one racquet to the next. Like equation (2), equation (3) is not a theoretical result. Rather, it is one that gives a good fit to experimental data obtained by measuring the swing speeds of different racquets and various other implements such as rods and baseball bats.

Effective Mass

The equation describing the ball speed is essentially the same as Eq. (1) but the relevant mass of the racquet is not its whole mass. It is not even the mass of the head. The relevant mass is the "effective" mass, M_e, which depends on the swingweight of the racquet and the impact point. The effective mass is smallest at the tip, largest at the throat and about equal to the mass of the head for an impact in the middle of the strings. It is also quite small at impact points close to the frame near the 3 and 9 o'clock points. It can be calculated by firing a ball at a particular impact point on the strings and measuring the incident and rebound speeds of the ball. Alternatively, it can be calculated at any given impact point from a measurement of the swingweight, as described in the Appendix.

Energy Loss

The outgoing ball speed also depends on how much energy is lost in the ball, the strings and the racquet frame. Energy loss in the strings is very small, while energy loss in the frame is due to frame vibrations. There are no vibrations for an impact at the sweet spot in the middle of the strings, but the racquet vibrates when the impact point does not coincide with the sweet spot. Stiff racquets vibrate less than flexible racquets so they tend to be more powerful. There is a simple formula that combines both the effective mass and energy loss at any given impact point. For a serve, that formula is

(4)      v = (1 +e_A)V

where v is the outgoing ball speed, V is the racquet speed at the impact point, and e_A is the "power potential" at the impact point.

Racquet Comparison

e_A is easy to measure or calculate for any given racquet. This web site tabulates values of e_A for over 1000 different racquets, at 15 different impact points on the strings. For example, consider a Babolat Pure Control racquet with a weight of 308 g and swingweight SW = 310. We can compare its power with say a Wilson Burn 100S racquet with a weight of 316 g and swingweight SW = 316. Both racquets are 27 in long, both have a similar head size, but the Wilson is stiffer and slightly heavier. The e_A values on the long axis are shown in Table 1 vs the impact distance, d, from the butt end of the racquet.

Table 1
d (inch)	16	19	21	23	25
Babolat	0.49	0.45	0.395	0.283	0.130
Wilson	0.54	0.47	0.407	0.304	0.175

If we calculate the swing speed from Eq. (3) then we get the racquet head speed in the middle of the strings at d = 21 inch. The speed near the tip will be proportionally larger, depending on how the player swings the racquet. For example, suppose the player swings the racquet in such a way that it rotates about an axis 5 inches beyond the end of the handle just before impacting the ball. If the ball is impacted at a distance d (in inches) from the butt end, then the impact point rotates in a circular arc of radius R = (d + 5). The velocity of the impact point is then V = Rw where w is the angular rotation speed of the racquet. Since V is given by equation (3), we find that

(5)      V = 170(d + 5) / (21 + 5)(SW)^1/4

The corresponding values of racquet speed V and serve speed v are shown in Table 2 and also in Fig. 3. The racquet speeds are almost identical since the swingweights differ by only 2%. The maximum outgoing ball speed is about 0.2 m/s faster with the Wilson since it is a stiffer and slightly heavier racquet so e_A is larger at all impact points. In both cases, the outgoing ball speed is a maximum at the middle of the strings or slightly towards the tip.

Table 2
d (inch)	16	19	21	23	25
Babolat V	32.7	37.4	40.5	43.6	46.7
Wilson V	32.6	37.2	40.3	43.4	46.5
Babolat v	48.7	54.2	56.5	56.0	52.8
Wilson v	50.1	54.7	56.7	56.6	54.7

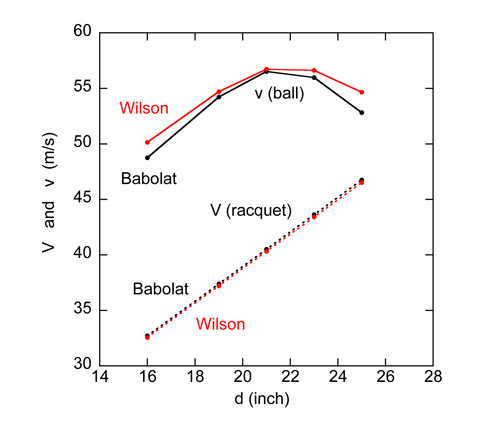
Figure 3 — Comparison of Babolat and Wilson racquets. d is the impact distance from the butt end.

Other Racquets

Measured values of e_A for 133 other racquets, all 27 inch long, and for an impact in the middle of the strings, are shown in Fig. 4. The correlation between e_A and racquet mass is very weak, but the correlation with swingweight is very strong. For this group of racquets, a smooth curve can be fitted to the data in Fig. 4. The equation describing that curve is

(6)      e_A = -0.2165 + 0.00277(SW) - 2.66 x 10^-6(SW)²

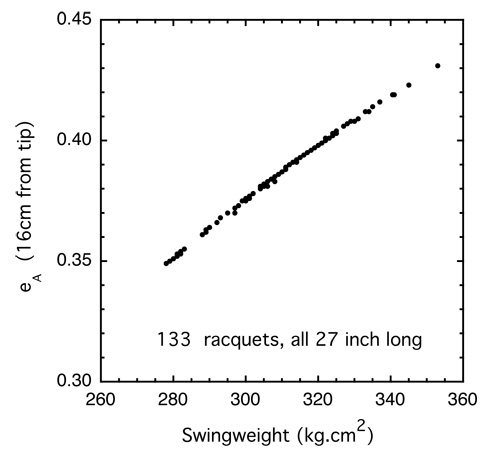
Figure 4 — e_A, vs swingweight for 133 different racquets all 27 inch long.

Combining equations (3), (4) and (6) gives the outgoing ball speed off the middle of the strings, for this group of racquets, as shown in Fig. 5. The serve speed varies from 54 m/s (121 mph) at the highest swingweight to a maximum of 56.2 m/s (125.7 mph) at SW = 320. However, from SW = 280 to SW = 360, the range of swingweights most commonly encountered, v varies by such a small amount that it is essentially constant. In other words, all the racquets shown in Fig. 4 are equally powerful for a maximum effort serve.

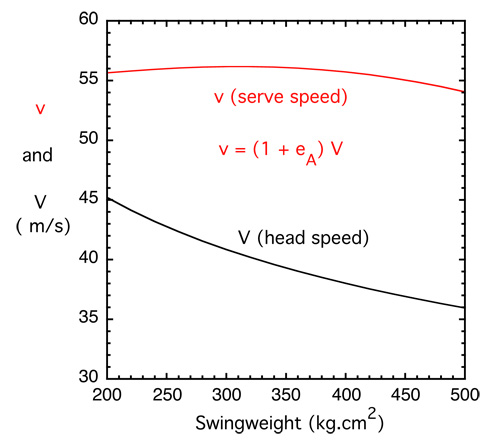
Figure 5 — Racquet head speed (V) and serve speed (v), vs swingweight

Groundstrokes

Equations (3) and (5) give the maximum swing speed for a typical player, using maximum effort. Most of the time, a player strikes the ball with less than maximum effort, so racquet power does not limit the speed of the outgoing ball in that case. It is the player who deliberately chooses to limit the ball speed. If a player wants to hit a groundstroke faster then the racquet can be swung faster, up to the maximum effort limit. Swinging a racquet faster requires extra effort, so a question arises as to whether a more powerful racquet might assist with groundstrokes, even if it has no significant effect on a maximum effort swing.

The formula for the outgoing ball speed in a groundstroke is

(7)      v_out = (1 + e_A)V + e_Av_in

where v_in is the incoming ball speed and V is the racquet head speed at the impact point. We can compare v_out for different racquets assuming either that the player swings the racquet at the same speed, or the player swings the racquet with the same effort. A racquet with a large swingweight will require a greater effort to swing it at a given speed than a racquet with a small swingweight. An increase in racquet head speed requires greater effort mainly because the arm needs to swing faster. Since the arm is much heavier than a racquet, and also has a much larger swingweight than a racquet, most of the extra effort involved is swinging the arm faster. To be consistent with Eqs. (2) and (3), a reasonable estimate of racquet head speed at half maximum effort is

(8)       V = 85 / SW ^1/4

which is half the speed given by Eq. (3). We can now calculate the outgoing ball speed from Eq. (7) for a typical case where the incoming ball speed is say v_in = 20 m/s. Taking the e_A values from Eq. (6), and racquet speed values from Eq. (8) gives the results shown in Fig. 6.

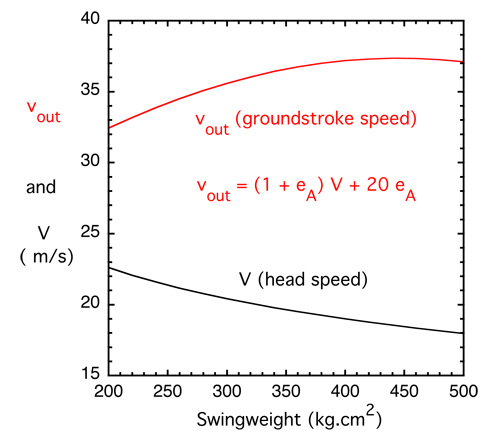
Figure 6 — Racquet head speed (V) and groundstroke speed (v_out), vs swingweight.

This shows that for a given effort swing, the outgoing ball speed increases with swingweight, even though the racquet head speed decreases when swingweight increases. The increase in the power potential e_A, combined with the extra bounce speed of the incoming ball, more than makes up for the decrease in swing speed when swingweight is increased. In that respect, racquets with a large swingweight are slightly more powerful for groundstrokes, even though all racquets are equally powerful for a serve.

Conclusion

For a maximum effort serve, the speed of the racquet at the impact point will depend on the swingweight. A racquet with a higher swingweight and more power will swing more slowly than a racquet with lower swingweight with less power. The net result is that the gain or loss from power potential tends to cancel the loss or gain from swing speed. Maximum serve speed is thus similar for all racquets. In a groundstroke, the player can usually choose to swing at a speed that requires less than maximum effort. In that case, and for a given effort, racquet head speed will be lower if the player uses a racquet with a higher swingweight. However, the power potential of a high swingweight racquet more than makes up for the lower swing speed, with the result that a groundstroke can be struck at a slightly higher speed with a high swingweight racquet.

Appendix

The effective mass of a racquet for an impact on the long axis of the racquet is given by the formula

(9)       M_e = M / (1 + Mb² / I_cm)

where M is the total racquet mass, b is the distance between the impact point and the centre of mass (i.e., the balance point) and I_cm is the moment of inertia for rotation about an axis through the center of mass. The swingweight of a racquet is measured about a different rotation axis, 10 cm from the butt end of the handle, and is given by SW = I_cm + Mh² where h is the distance from the swingweight axis to the center of mass. The value of M_e can be calculated for any racquet and any impact point. The result (in kg) is given very closely by the formula

(10)       M_e = SW / R²

where R = h + b is the distance (in cm) from the swingweight axis to the impact point, as shown in Fig. 7. A graph of M_e vs SW is given in Fig. 8 for impact points at R = 30, 40 and 50 cm. In practice, most racquets have a swingweight between 250 and 400 kg.cm2.

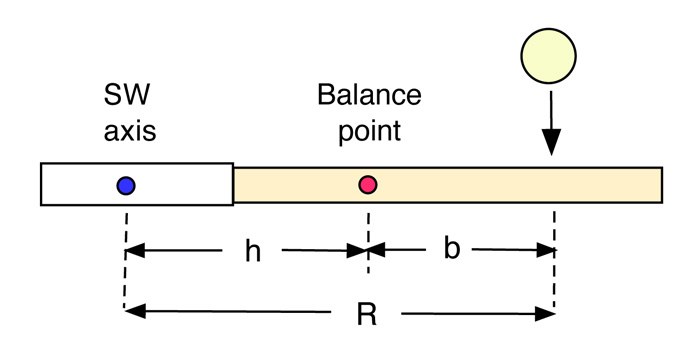
Figure 7 — Definitions of b, h and R.

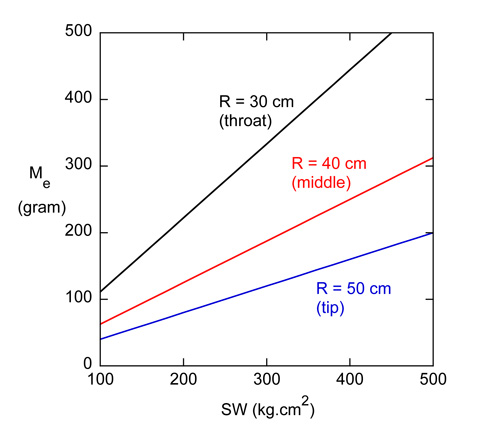
Figure 8 — Effective mass, M_e, vs swingweight

A realistic calculation of the outgoing ball speed from a racquet requires an estimate of the energy that is lost in the ball and the racquet when the ball bounces. The energy lost in the strings is almost negligible by comparison since the strings are very elastic and return around 90% of their stored elastic energy to the ball. On the other hand, the rules of tennis insist that the ball must lose about 45% of its energy when it bounces on a hard surface, or about 20% of its energy when it bounces off the strings. Energy is lost in the racquet frame as a result of frame vibrations, but the energy loss is negligible for an impact in the middle of the strings since then the racquet doesn't vibrate. The total energy loss can be described by a quantity known as the coefficient of restitution, e, which would be 1.0 for a perfectly elastic collision. For an impact of a ball with the strings of a racquet, e is typically about 0.8 in the middle of the strings and decreases to about 0.5 near the racquet tip or throat. For a collision between the racquet and the ball, the outgoing ball speed for a serve is given by

(11)       v = (1 + e)M_eV /( M_e + m)

which is the same as Eq. (1) when e = 1 and when M_e is replaced by M. Equation (11) is slightly complicated because it combines both the coefficient of restitution, e, and the effective mass, M_e into the expression for v. A simpler expression for v results if we let

(12)       v = (1 + e_A) V

where e_A is called the apparent coefficient of restitution or the "power potential" at the given impact point. If we compare Eqs. (11) and (12), it can be shown that

(13)       e_A = (eM_e - m) / (M_e + m)

e_A is easily measured since it is equal to the ratio of the rebound speed to the incident speed for a ball incident at right angles to a racquet that is initially at rest.