1. INTRODUCTION
The tennis world has gone topspin crazy and players want equipment that maximizes spin. Over the years there have been many theories as to what equipment configurations, primarily with respect to the stringbed, increase spin. It has been maintained that spin is increased by a
- Open string pattern for more ball embedding and friction.
- Closed string pattern for more surface contact and friction.
- Stiff stringbed causing more ball squashing and surface area contact and grabbing.
- Soft stringbed providing a longer dwell time for friction to work.
- Thin gauge strings for more grabbing and embedding.
- Rough, textured, shaped, or sticky strings to increase ball-string friction.
- High friction between strings because string movement thought to lessen grabbing.
- And most recently, strings that move and stretch laterally in the stringbed and snap back give the ball extra spin.
Interestingly, all these, except the last, concentrate on the friction between the ball and the strings. Friction does indeed do most of the work, but it does about the same amount for every string and stringbed configuration. It is not the difference maker. There is evidence that indicates that it could be the lateral movement of strings that contributes some, all, or a significant portion of the spin difference between strings (see the TWU article Which Strings Generate the Most Spin. So the question becomes, “what stringbed properties contribute to lateral string movement?” One obvious candidate is the friction between strings. Strings with the lowest inter-string friction should be easiest to move. The TWU articles “Spin and Static Friction” and “Spin and Sliding Friction” address this.
Another candidate is string pattern. That will be our concern here. “Pattern” usually refers to the number of mains and crosses in the racquet. This affects the spacing between the strings. In turn, it affects stringbed stiffness, inter-string friction, and ball embedding (in the sense of squeezing between and pushing the strings, not in the sense of friction). These will all be addressed to some extent in what follows.
2. THE EXPERIMENT
To examine this issue, we will take the stringbed apart and put it back together again, string by string, analyzing the consequences of adding additional strings as we proceed. We will examine string patterns in three ways: using (1) a ball swinging as a pendulum onto one or two strings, (2) a specially constructed “string pattern rig” and (3) a tennis racquet. The rig was used because it allowed fast pattern changing, controlled string spacing, less string usage, and generally more experimental flexibility. It is not necessary to string an entire racquet with the typical 16x18 or 16x19 patterns to examine the effects of string spacing. The pattern rig therefore had a maximum configuration of 13x8. Figure 1 displays the patterns tested in the rig. The “mains” are the horizontal strings that do the sliding up and down, and the “crosses” are the vertical strings. The distinction is made depending on the direction of the ball across the strings. The ball moves perpendicular to the mains in the plane of the stringbed and parallel to the crosses.

Figure 1 — String Patterns and Spacing. Balls were aimed at the center of the stringbed where the pattern of interest was located. In some cases, such as the 8Mx4X, 8Mx8X, and 13Mx8X, that meant the impact area was very similar in terms of spacing, and the big difference was in the number of strings creating interstring friction. The 8Mx6X was somewhat similar to the 8Mx2X in the central spacing (though actually greater), but had more strings and more friction. Depending on the exact location of an impact, the ball had more or less contact with the underlying mains.
For the pattern rig tests, the rig hung vertically and was allowed to recoil on impact. Balls were launched onto the rig at different angles with backspin by use of a ramp inclined at preset angles. All impacts were filmed at 420 frames per second. Launch speeds ranged from 2 m/s to 5 m/s, depending on the angle. Due to these slow impact speeds, the patterns were all strung at a low tension of 32 lbs in order to ensure string movement and to produce a long enough dwell time to capture several video frames with the ball on the strings. All patterns were strung with Prince Synthetic Gut 16 with Duraflex.
The rig was also used in a different configuration that allowed the ball to be incident with topspin onto the racquet (this is the situation when you hit the ball on the rise or when you hit with slice). This was accomplished by placing the rig flat on a table and using the same inclines to roll the ball onto the strings. In this case the string rig had springs attached to its underneath so the rig could recoil on impact, as in an actual tennis hit. These results are not reported here, however.
Two racquets were used in the racquet tests: a Prince Graphite Tour 600 and a Volkl Classic 10 Pro. The Graphite Tour was chosen because of its open 14x18 pattern and the Classic 10 Pro for its closed 16x19 pattern. The Graphite Tour pattern was made even more open by skipping every other cross string resulting in 23 mm spaces between crosses and 10 mm between mains. This configuration was strung at two tensions — 35x55 pounds and 58x58 pounds. The Classic 10 Pro was strung at 58 x 58 pounds and had mains 8mm apart and crosses 12mm apart. The two racquets are shown in Figure 2.

Figure 2 — Racquet String Patterns and Spacing. Prince Graphite Tour 600 with every other cross string skipped, resulting in a 14x9 pattern with 10mmM x 23mmX spacing (left) and Volkl Classic 10 Pro with 16x19 pattern with 8mmM x 12mmX spacing(right).
3. REBOUND MODEL AND GEOMETRY
The model and terminology for impacts onto the patterns are represented in Figure 3.
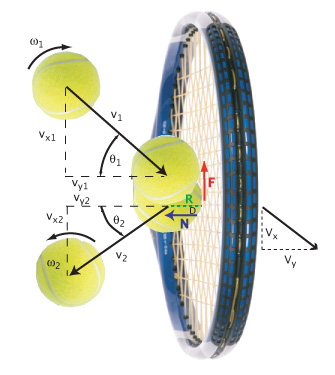
Figure 3 — Bounce Model. Bounce model for ball incident on strings with backspin, sliding across (down) the main strings, and rebounding with topspin.
The symbols represent the following parameters:
- ω1 — The angular velocity (spin) of the incident ball (radians/sec).
- ω2 — The angular velocity of the rebounding ball (radians/sec).
- v1 — Incident velocity of ball (m/s).
- v2 — Rebound velocity of ball (m/s).
- vy1 — Component of incident velocity perpendicular to stringbed (m/s).
- vy2 — Component of rebound velocity perpendicular to stringbed (m/s).
- vx1 — Component of incident velocity parallel to stringbed (m/s).
- vx2 — Component of rebound velocity parallel to stringbed (m/s).
- θ1 — Incident angle measured from perpendicular to stringbed (degrees).
- θ2 — Rebound angle measured from perpendicular to stringbed (degrees).
- F — Friction force acting opposite to the direction of the bottom of the incident ball (Newtons).
- N — Normal reaction force of strings on ball (equal and opposite of force of ball on strings) (Newtons).
- R — Radius of ball = .033 m.
- D — The offset distance between a radius to the center of mass and the net action of the normal force (mm)
- Vx — Component of racquet impact point rebound velocity parallel to stringbed (m/s).
- Vy — Component of racquet impact point rebound velocity perpendicular to stringbed (m/s).
For our purposes here, there are three equations that are important and which we will use in the analysis:

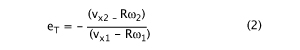
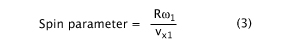
eA is the apparent coefficient of restitution and eT is the apparent tangential coefficient of restitution. eA is a calculation of the energy return perpendicular to the stringbed and eT of the energy return tangential to the stringbed. eA can range from 0-1.0, but for an impact in the middle of the strings of a hand-held racquet, eA is typically about 0.4-0.5. eT can vary from -1.0 to 1.0 but is typically about 0.01 for a hand-held racquet. The spin parameter with a subscript of 1 is the ratio of the velocity of the incident spin in m/s divided by the incident velocity of the center of mass of the ball in the direction parallel to the strings ( subscript of 2 indicates the same for the rebound). This parameter will be used extensively in the graph analysis below as explained in Section 6.
4. SINGLE AND DOUBLE STRING IMPACTS
First, let's look at a ball swinging as a pendulum with a bit of backspin impacting a single string. The intended “stringbed plane” is from left to right in the video, in which case the ball would normally bounce up toward the top. However, with just one string, the ball can impact to one side or the other of the string such that the impact plane effectively gets tilted to one side or the other, and the ball bounces accordingly. You can see that a single string can create a lot of spin, but the bounce angle can be very unexpected vis-a-vis the assigned frame of reference of “hitting” the ball toward the top.
Movie Screen 1 — Single string bounces. The ball is free to impact at many angles onto the string. It is not impacting a flat string plane but rather a convex string surface. The rebound can occur in many directions. This is important to remember when we look at some of the patterns below where the ball has maximum access to single strings in the stringbed. (Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
As soon as you add a second string perpendicular to the first, you have taken away most of the bounce possibilites except those above the plane described by the two strings (as long as you hit in the intersection of the strings). We have added a dimension of control, but still the bounce goes off at unexpected angles because the ball can still contact a bit to the side of each string, causing a radical string deflection which pushes the ball one way or another as it snaps back. This is displayed in the next selection of movies.
Movie Screen 2 — Double string bounces. A bit of control is added to the rebound as the impact surface becomes more planar at the string intersection. (Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
We are still getting plenty of spin but there are still control issues if the ball hits too far off the axis of either string. However, from these single and double strings examples we can see how strings behave by themselves and how that behavior begins to get altered as strings are combined.
5. PATTERN-RIG EXPERIMENTS
It's time to start building more complicated patterns. Two sets of videos were taken separately in different trials. One set was taken at about 45 degrees to string plane and another set from the side. The first set was used to view string movement and the second set was used to measure and calculate speeds, spins, and angles.
The videos in Movie Screen 3 below are for bounces from each pattern setup at an approximate impact angle of 60 degrees from perpendicular to the stringbed. These videos were filmed from the side to accurately see (and measure) spin, speed and angle of rebound.
Movie Screen 3 — Spin at 60 degrees. Impacts and rebounds at approximately 60 degrees from perpendicular for each string pattern.
Table 1 displays the spin for each pattern at 60 degrees, as shown in Movie Screen 3.
| Mains Number | Crosses Number | Mains Spacing (mm) | Cross Spacing (mm) | Spin (radians/sec) |
|---|---|---|---|---|
| 0 | 8 | none | 10 | -20.5 |
| 0 | 4 | none | 20 | -13.2 |
| 8 | 8 | 20 | 10 | 6.3 |
| 8 | 4 | 20 | 10 | 10.7 |
| 8 | 2 | 20 | 20 | 20.2 |
| 8 | 6 | 20 | 30 | 42.4 |
| 13 | 0 | 10 | none | 42.7 |
| 8 | 0 | 20 | none | 54.1 |
Table 1 — Spin vs pattern and spacing. Comparing the rebound spin for different string patterns and spacing at an impact angle of approximately 60 degrees. A negative spin means that the inbound spin was not turned around into topspin — the backspin was reduced but the ball still rebounds with backspin.
Table 1 indicates some striking relationships:
- Cross strings by themselves do very little to change spin, as is evident from the 0M x 4X and 0M x 8X patterns.
- With mains present, fewer crosses = more spin.
- Greater main spacing = more spin.
- Greater cross spacing = more spin.
If we look at the same patterns again at an impact angle of 60 degrees (note: videos of 0M x 4X and 0M x 8X were only filmed at 40 degrees but are included here to get a qualitative understanding of how they react) from perpendicular but from a slightly different angle, we can see how the strings move on the ball. Pay close attention to the connection between main string movement and the resulting spin.
Movie Screen 4 — String movement at 60 degrees. Impact and rebound onto each pattern from the 60 degrees to normal launch ramp. Patterns are listed in order of increasing topspin rebound. (Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
You can see that when you can see a main string move, the ball rebounds with topspin. If no main moves, there's very little or no visible topspin. And when there are no mains, there is negative spin. These results correlate exactly to the measured results from Table 1.
The correlation between string movement and the amount of topspin for each pattern at each angle of impact can be seen in Movie Screen 5.
Movie Screen 5 — All impact angles. Impact and rebound onto each pattern from each launch ramp (20, 30, 40, 50, 60, and 70 degrees). (Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
6. PATTERN-RIG ANALYSIS
The experimental apparatus was setup to create similar impacts on each string pattern at various angles. But the setup creates some complications for presenting the data in the usual graphical format. As you raise the angle of the incline, the ball will roll faster and the spin will decline. Consequently, each target angle has a different incident speed and spin from each other, but at any particular angle, all the patterns were being compared using the same input variables. But in many cases this makes displaying the results graphically a bit confusing. Usually, when you read a graph, you are looking at the relationship of how one variable changes when you change another, all else remaining the same, and you can make statements such as “as x increases, y decreases.” But when all the input variables change, you can't easily do that. To alleviate this problem, the following graphs plot ratios of incident and rebound parameters against each other. For example, because incident spin and speed (specifically the incident speed tangential to the stringbed in the direction of the ball, vx1) are both dependent on the incline angle, using the ratio of spin speed to tangential speed as the x axis variable implicitly includes all three spin input variables (spin, speed, and angle) in one fell swoop.
The other complication with the setup involved the varying free fall distances undergone by the ball after leaving the incline. As can be seen in the videos, each impact angle required that the pattern rig be horizontally and vertically moved to a fixed location so that the ball would clear the ramp both upon impact and during rebound. This free fall trajectory changed the actual impact angle compared to the incline plane. It also meant that acceleration due to gravity while the ball was on the strings might affect the results, so a correction was made for that acceleration.
All that being said, the differences in pattern performance are so striking that they almost transcend the need for interpretation. It is simply obvious that pattern does make a difference on spin and rebound angle under the conditions introduced in the experiment. In the graphs that follow, Figures 4-7, you will notice that each color curve tends to maintain its relative location to all the others in each figure. Sometimes curves cross each other and change relative postion. This is due to the ball sometimes impacting more exactly into the open space getting access to the a "naked" main. That will cause greater spin and launch angle. But on average the curves maintain their relative positioning.
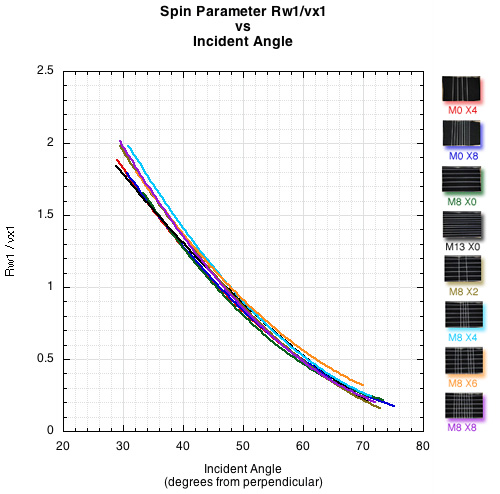
Figure 4. This graph depicts how, in this experimental setup, incident spin and tangential speed vary as the incident angle varies. As the incline ramp angle increases the incident spin decreases and the incident speed increases. The rebound spin and angle depend on all three of these parameters.
The spin ratio on the y axis is the speed of the spinning ball at the contact point with the strings, Rω1, where R=.033m which is the radius of the ball, and ω1 is the angular velocity (spin velocity) in radians per second, and vx1 is the linear speed of the CM of the ball in the direction it travels across the main strings.
The graph lines for the different patterns differ primarily from experimental vagaries such as slightly different starting location on the launch ramp.
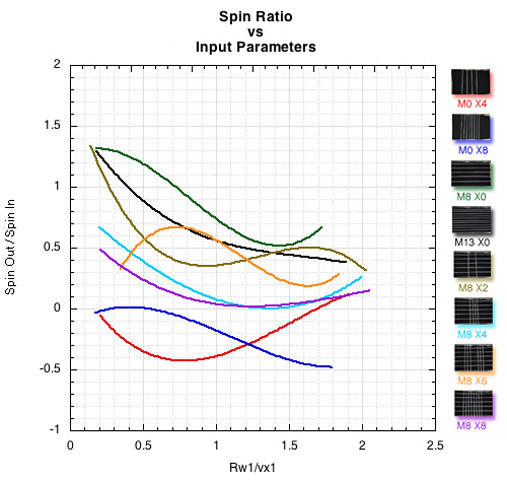
Figure 5. The ratio of spin out to spin in is used here on the y-axis to highlight the fact that spin out depends on spin in. The more the incident backspin, which occurs at the lower launch incline angles, the less the outgoing topspin, and the less the incident backspin (at the steeper ramp angles), the more topspin will be created.
From top to bottom, the most spin is produced by the easiest acces to the mains. This is facilitated by either no crosses, fewer crosses, or larger spaces between crosses. The pattern of M8 X6 is a special case of a lot of strings but a large space at the impact point allowing the ball access to the mains. The variability in the orange line, as with all others, is a consequence of exactly where on the stringbed the ball impacted. If the main was struck at just the right angle, more spin was produced.
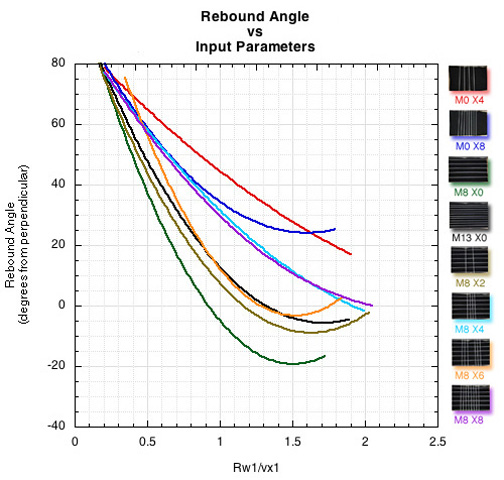
Figure 6. As with spin in Figure 5, the pattern with more access to the mains produces the steepest launch angle leaving the rig (racquet). The angles in the graph are relative to perpendicular to the stringbed which is the horizontal in all the movies.
A high angle from perpendicular means a rebound toward the bottom of the screen (thus, a low launch angle from the strings toward the direction of the opponent). A negative rebound angle means the rebound bounced back toward the direction it came in from — it actually rebounded toward the top of the movie frame, which is a high launch angle in the court frame of reference. Thus, the launch angle to the court increases from top to bottom in the graph and those curves lying below others launches more steeply than the others.
The fewer the crosses and wider the spaces, the closer the rebound angle is to the horizontal.
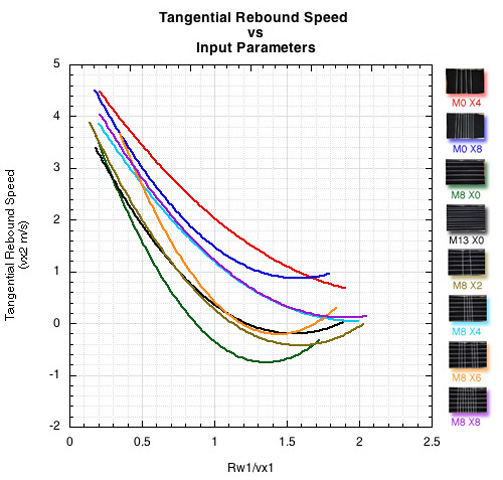
Figure 7. This is really another perspective on Figure 6. As the ball travels across the strings (from top to bottom in the movies), friction and lateral snapback by the strings slows the ball in that direction. The more the ball is slowed, the steeper the launch angle will be (remember, in Figure 5, lower angles on the y-axis means steeper angle in the court reference frame).
The fewer the crosses, the greater the spaces, the more the ball will slow across the strings and the closer the rebound angle will be to horizontal.
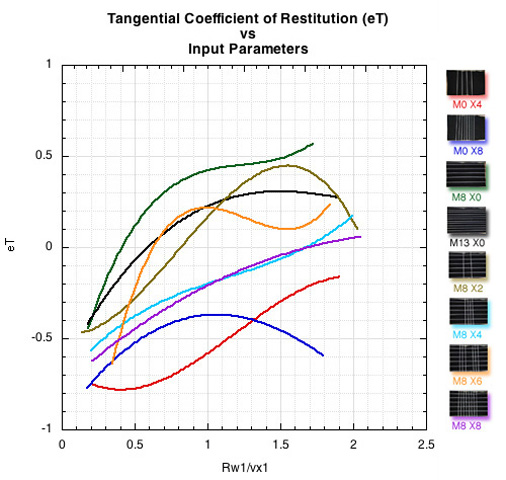
Figure 8. Apparent tangential coefficient of restitution is defined in Equation 2 as eT = -(vx2 - Rω2) / (vx1 - Rω1), where R=.033 m, the radius of the ball, ω2 is the angular velocity of the rebound, vx2 is the tangential speed of the rebound at the center of mass (CM), ω1 is the incident angular velocity, and vx1 the incident tangential velocity of the CM.
In other words, eT is the ratio of the net speed of the bottom of the ball just before impact to that after impact. When the ball impacts with backspin, the spin speed and the tangential CM speed add (the denominator). When the ball rebounds with topspin the ball is spinning in one direction and traveling in the opposite, so we subtract the spin speed from the linear speed.
We have our typical pattern of curves: the eT increases as you decrease crosses and open the spaces between acrosses and mains.
7. RACQUET PATTERN EXPERIMENTS
As described in Section 2, three patterns were use— a 14Mx9X pattern strung at 35x55 pounds and 55x55 pounds with polyester and a 16Mx18X pattern strung with nylon at 58x58 pounds. Changing the tension in the 14x9 pattern allows us examine the difference a stiffer main string would make. Would increased interstring friction inhibit spin? Would the added force that accompanies higher stiffness help overcome interstring friction and also facilitate a more timely and forceful snapback to spin the ball? Movie Screens 6-8 present the results at each launch ramp angle for the 14Mx9X pattern at 35x55 pounds ('open-low tension'), 14Mx9X pattern at 55x55 pounds ('open-high tension'), and 16Mx18X pattern at 58x58 pounds ('closed-high tension') racquets.
Movie Screen 6. Impact and rebound onto each racquet pattern from each launch ramp (20, 30, 40, 50, 60, and 70 degrees). (Note: To see stringbed interaction, movies are best viewed frame by frame using keyboard arrow keys or movie controls.)
In virtually all the moveis in Movie Screen 6 you can see string movement in the open-low and open-high patterns but not in the closed-high pattern (though it is difficult to clearly see the strings as well in the closed-high pattern). It also visually appears that there is more spin coming from the open patterns in all cases.
8. RACQUET PATTERN ANALYSIS
The following graphs confirm our visual evidence that the open patterns prodcue more spin than do the closed pattern. This is the same result as in the pattern rig experiment. But which open pattern produces the most spin?
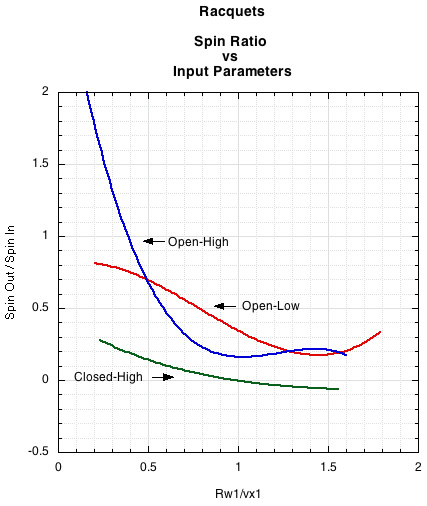
Figure 9. Both the open patterns demonstrate more spin at all input values. The curve is also much less variable. There was much less scatter of the raw data points than with the open patterns, indicating a more consistent, predictable rebound (see Figure 10).
The two open patterns had more scatter on the data points and less predictability of rebound. This tends to distort the best fit curve and make analysis more difficult. However, to eliminate such data would be to eliminate an essential feature of what an open pattern does—it introduces a random variability into the spin result. When a main string is hit just right, a much greater spin than average is produced. The very high spin ratio values for the open-high racquet at high angles may have been due to a coincidence of perfect alignment of imapact angle to main strings.
However, where the spin parameter is 0.6-1.1 (impact angle of about 42-55 degrees as shown in Figure 4) the curves separate and the scatter minimal. Using this data, one is tempted to say that lower tensions increase spin in the same pattern at impact angles achievable for very heavy spin shots.
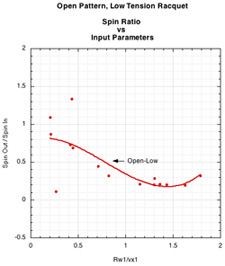
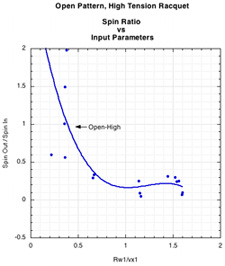
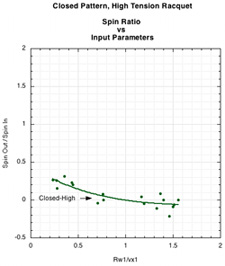
Figure 10. Raw data points for the patterns shown in Figure 9. For the open patterns, the significant scatter occurs mainly at very low Rω1/vx1, which occurs at the larger angles from perpendicular (or skimming angles onto the strings as seen in Figure 3). These are not typically angles of impact you will encounter in normal tennis strokes, so the separation of the curves here is not as important and the scatter not as much of a concern.
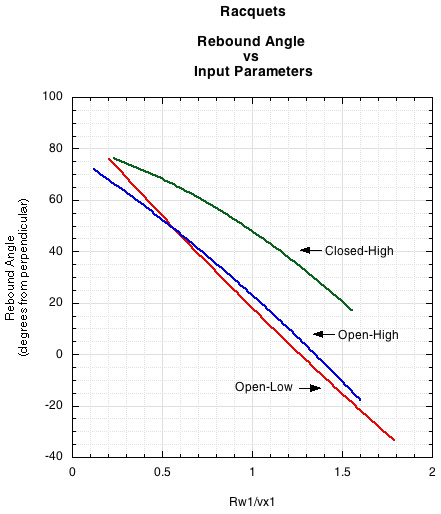
Figure 11. The open-low tension pattern had a slightly higher rebound trajectory than the open-high. The closed-high tension pattern clearly has lower trajectory rebounds. The y-axis is the angle from perpendicular to the racquet, so a high number means it is rebounding more toward the ground. A low number means it is rebounding more horizontally, and a negative number means the ball is rebounding back in the same direction it came from and thus above the horizontal perpendicular to the racquet.
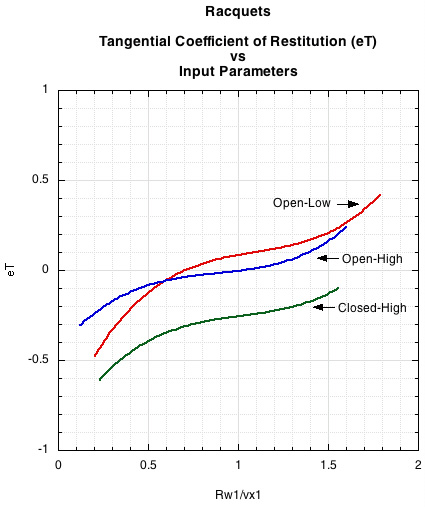
Figure 12. The open patterns are once again separated from the closed pattern. The closed pattern returns much less tangential energy to the ball. The closed 16x18 pattern was also strung at a slightly higher tension (58 lbs) than the 14x9 at 55 lbs, and it was strung with a string with a higher coefficient of friction. So we can't blame it all on pattern, but rather a combination of factors is at least partially responsible for the decrease in spin.
9. DISCUSSION AND CONCLUSION
This results of these experiments strongly suggest that alterations to one's string pattern can influence spin. The more open the pattern, especially the cross strings, the more access the ball has to the main strings in order to tangentially stretch them and store and return tangential energy, increasing spin-producing torque and rebounding the ball at a higher angle. Figure 13 below shows a simple summary of spin vs incident angle for each pattern tested but without all the technical ratios presented above.
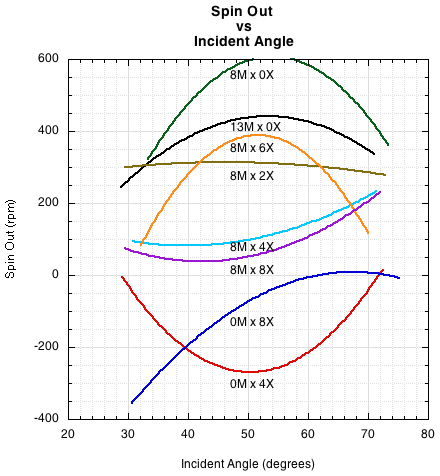
Figure 13. This graph shows the "uncorrected" curve fits for spin produced by each pattern at each angle. It portrays the same results as the figures above with no attempt to take into account variance in input variables. Thus, its presentation is as we usually understand spin. Points below zero indicate that the spin is not turned around by the strings. As in the graphs above, the fewer crosses and/or the wider the spaces between crosses, the greater the lateral stretch/movement of the main strings and the greater the spin produced.
The term “string movement” is often used to describe what is occurring during this tangential phase of impact. However, movement is a manifestation of stretching. The important event is not that you are moving the string but that you are stretching tangentially to the stringbed. That is how the energy gets stored. The term “movement” arose because the tell-tale sign of its existence came from observing the dislocation and sticking of the main strings. Sticking was an undesirable side-effect and movement was thus considered a bad thing.
But the more the string moves, the more it stretches. If friction locks it in place, the length of string that is stretched is only that in the space between the cross strings. This is a very stiff and short section, will not stretch much, and will not store much energy. If the interstring friction is low enough, the string will break free, effectively doubling, tripling (or much more) the length of the string section that is stretched, and with it, increasing the amount of energy stored. If the energy is returned to the ball before it leaves the strings, then there will be more spin. So the mains must break free and move along the cross strings and stretch at the same time. Movement and stretch is a complementary process.
An open pattern facilitates tangential stretching because there are fewer strings to add to interstring friction and it gives the ball access to the main in ways that allow the ball to push the strings aside. A low tension might also facilitate that process, but the evidence obtained in the tests with the 14x9 pattern strung at low and high tension was not conclusive enough to make such a definitive statement. The higher tension on the closed 16x18 racquet pattern produced significantly less spin, but it appears that it was the pattern more than the tension (and material) that contributed to this decrease. In any event, more investigation into the role of tension is required.
The tests in this experiment were mostly performed at low tensions so a blanket statement cannot be made for results at all tensions. However, the impact speeds and forces were also very low. Thus it is reasonable to expect that the same results will be seen at much higher impact forces, even if the string tension is higher. Nonetheless, with the recent interest in the use of polyester strings at much lower tensions (30-50 pounds), these tests have direct relevance to those setups. The anecdotal playtest evidence from these setups is that spin is greatly increased at low tension (see thread in TW Talk Tennis message board: “Low, low tensions. 30lbs feels great. 20lbs pretty good, too”). The corollary, of course, is that spin is reduced at high tension.
The second half of the movement phase is that the string must snap back into position before the ball leaves. There must be enough energy left in the string to overcome interstring friction in its return journey and to do so quickly enough to influence spin. Tension and/or string stiffness may play a role here too.
It is safe to say that pattern makes a difference (at least for the low-impact conditions tested in this experiment). But questions remain as to how to maximize or optimize that difference. Choosing strings with a low coefficient of friction should help. The racquet pattern tests in Section 7 inconclusively suggest that lower tension might also help. Also, how much difference in string spacing is enough or not enough to make a meaningful difference? There was very little comparative spin production with the 16x18 pattern compared to the 14x9. What about 16x16, 16x14, 16x12? And where the spaces occur matters also, especially as demonstrated in the 8Mx6X pattern in the pattern-rig tests. The pattern contained a lot of strings, but the impact zone was left open and the pattern generated a great deal of spin. Perhaps, in this way, spin, control, and feel can be better customized to each player.

