INTRODUCTION
Ever since tennis was first introduced as a serious sport, players have been blaming their racquet or the ball for the mistakes they make. That is why professional players need six identical racquets each match, all freshly strung, and why each ball is closely inspected for fluffiness before it is deemed suitable to be served. Any tiny variation is enough to throw even a professional off balance. How then do players cope with changes in air pressure and temperature and humidity? All of these factors affect the flight of a ball through the air, so they affect where the ball lands. If players were really serious about their sport, then they should bring at least a barometer and a thermometer with them in order to fine tune their match-winning strokes. For that matter, a micrometer and a set of weighing scales would also help, since the flight of the ball also depends on its mass and its diameter.
If all of the above factors conspired in the worst possible way, then it would make a difference of around six feet in where the ball lands. That assumes the player hits the ball perfectly, at just the right speed and angle, and with just the right amount of topspin, to land on the baseline. And it assumes that the player has made allowance for the prevailing wind speed and direction.
The effect of changes in the weather and the ball can be demonstrated by calculating the trajectory of a ball under standard conditions and then varying all of the above factors one at a time. For example, suppose that we take the standard conditions to be no wind, a temperature of 70 F, air pressure = 30 inch Hg, and humidity = 50%, so the air density is 1.197 kg/m3. For our standard ball, we can assume that ball mass is 58 gram, ball diameter is 66 mm, next to no fluff on the ball, and the drag coefficient is CD = 0.51. The player strikes the ball at a height of 3 feet, directly above the baseline, at a speed of 70 mph and imparts 2000 rpm of topspin. In order to land on the opposite baseline, the ball needs to be projected at an angle of 11° above the horizontal, assuming it travels at right angles to the net rather than across court.
A short summary of the effect of changing each factor is presented in the table below.
| Effect of changing each variable | |||
| Factor | Value | Change to | Result |
|---|---|---|---|
| Launch speed | 70 mph | 75 mph | 6.6 ft long |
| Top spin | 2000 rpm | 1500 rpm | 4.0 ft long |
| Launch angle | 11° | 12° | 3.8 ft long |
| Launch height | 3 ft | 4 ft | 2.8 ft long |
| Drag CD | 0.51 | 0.6 | 2.6 ft short |
| Ball mass | 58 g | 56 g | 1.1 ft short |
| Diameter | 66 mm | 68.6 mm | 2.4 ft short |
| Density | 1.197 | 1.25 | 1.3 ft short |
| Density | 1.197 | 1.00 | 5.4 ft long |
| Headwind | 0 | 5 mph | 4.8 ft short |
| Tailwind | 0 | 5 mph | 5.0 ft long |
If each value in the Value column is unchanged, then the ball will land on the baseline, 78 feet from the launch point. If any factor is changed, then the ball will land long or short. A surprising result is that ball mass has a relatively small effect. If ball mass is reduced then it can be struck at a slightly higher speed, but only one factor is changed at a time in the table above. Lowering the ball mass means that it slows down more through the air, given that the drag force stays the same when only the ball mass is altered. Increased fluffiness acts to increase the drag coefficient, CD, so it increases the drag force. An increase in ball diameter will act to increase both the drag and the lift forces.
VARIATION IN BALL PROPERTIES
The rules of tennis specify that an approved ball must weigh between 56.0 g and 59.4 g, and its diameter must be between 65.4 mm and 68.6 mm. Also, it must bounce to a height between 53 and 58 inches when dropped from a height of 100 inches onto a hard surface, at a controlled temperature of 20 C (68 F). High altitude balls must bounce to a height between 48 and 53 inches, but they are the same mass and diameter as other balls and the flight through the air is quite different at high altitude. On a hot day, all balls will bounce a few inches higher, and will also bounce faster off the strings of a racquet.
CHANGES IN WEATHER
The flight through the air is determined by the drag force acting backwards on the ball and it also depends on the lift force, both of which depend on the air density. The lift force can be controlled by the player since it increases with the amount of topspin, backspin or sidespin. The lift force can act upward or downward or sideways depending on the spin direction. The air density depends on the air pressure, temperature and humidity, as shown in Fig. 1.
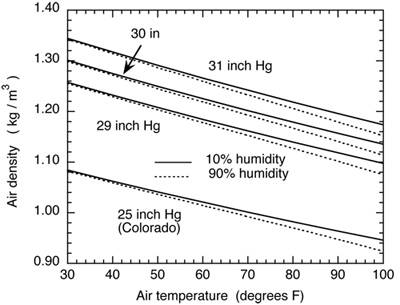
Figure 1 — Air density vs temperature, pressure and humidity.
At sea level, the air pressure is typically about 30 inch Hg, but in Denver, Colorado it is typically about 25 inch Hg. At any given location, air pressure varies by around 0.5 inch Hg depending on the weather. Weather bureau records are very misleading in this respect, since they alter the actual pressure readings to equivalent sea level pressures so that high and low pressure readings can be compared directly across the country. The actual air pressure, p, at an altitude h is given approximately by p = p0e-h/h0 where p0 is the pressure at height h = 0, and h0 = 4.6 mile = 24,280 ft. So, if h = 5,000 ft, p = 0.81p0. Air density varies with height in the same way if the temperature is constant. That is, at a height of 5,000 feet, the air density is 0.81 times the value at sea level.
BALL SPEED FORMULA 1
If a ball is struck at horizontal speed v0 then it would travel a horizontal distance s = v0t in time t if it didn't slow down through the air. However, it does slow down and the actual speed v after time t is given to a good approximation by
v = v0 / (1 + kCDs)
where k = πD2ρ/(8m), D is the ball diameter in m, ρ is the air density in kg/m3, m is the ball mass in kg, and CD is the drag coefficient. For a standard 66 mm diameter, 58 g tennis ball, kCD = 0.020m-1 when CD = 0.57 and ρ = 1.20 kg/m3. Over a distance s = 18 m, the ball speed drops to v = 0.735v0, regardless of the initial ball speed. The same ball in Colorado, with kCD = 0.016 slows to v = 0.776v0 after a distance s = 18 m.
BALL SPEED FORMULA 2
It is shown in our book The Physics and Technology of Tennis that the outgoing ball speed of a ball off a racquet is given by
vout = (1 + eA)V + eAvin
where V is the speed of the racquet head, eA is the apparent coefficient of restitution and vin is the incoming speed of the ball. For most racquets, eA is about 0.28. It is given by
eA = (e - m/Me) / (1 + m/Me)
where e is the actual coefficient of restitution, m is the ball mass and Me is the effective mass of the racquet at the point of impact (usually about 120 g). From these equations it is possible to work out the change in ball speed when m is reduced from 58 g to 56 g in the above table. The answer is that the ball speed increases from 70 mph to about 71 mph, in which case the ball would land about 1.3 feet long. But since the lighter ball slows down more through the air, and would land 1.1 feet short if struck at 70 mph, the end or combined result of reducing the ball mass from 58 g to 56 g is that the lighter ball will land about 0.2 feet (2.4 inches) long.
When a tennis ball bounces off the court, the value of e is about 0.8. Off the strings of a racquet, the value of e is about 0.9 since about half the impact energy is stored in the strings and most is given back to the ball. The energy loss is therefore reduced, so e is larger. High altitude balls have a lower value of e. Suppose that e = 0.8 off the strings, then eA will decrease from 0.28 to 0.21 and the speed of the ball off the racquet will decrease to 65 mph. This will compensate to a large extent for the thinner air at high altitudes, although the ball will bounce to a smaller height off the court.
EFFECT OF WIND
If the ball is traveling into a horizontal headwind, then the speed of the ball relative to the air is increased. As a result, the drag and lift forces on the ball increase. In addition, the directions of the drag and lift forces change so that they are more closely horizontal. These effects are shown in Fig. 2.
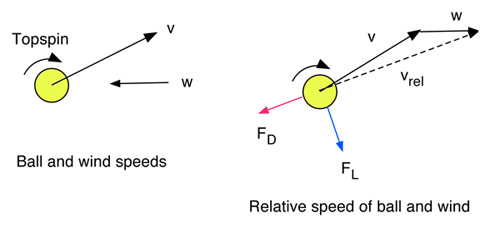
Figure 2 — When a ball at speed v meets headwind at speed w then the relative speed of the ball and the air increases to vrel. The direction of the drag force, FD is opposite the relative speed rather than being opposite the ball speed. The lift force, FL, is perpendicular to vrel.
HIGH ALTITUDE BALLS
High altitude balls approved by the ITF bounce to a height between 48 and 53 inches when dropped from a height of 100 inches and are not as stiff as other approved balls since the air pressure inside the balls is lower than usual. However, those figures refer to tests done at sea level. If the balls are taken to a location one mile high where the air pressure is lower than at sea level, then the balls will expand and become stiffer. The effect is the same as pumping extra air inside the ball to make it stiffer. Since the rubber deforms less, there is a smaller loss of energy in the rubber, so the balls will bounce between 53 and 58 inches like a normal ball. Since the air is thinner, the ball hits the court at a slightly higher speed when dropped from a height of 100 inches, and it slows down slightly less when it bounces. The combined effect of the increased bounce speed and the increase in stiffness means that a high altitude ball bounces about the same at high altitude as a normal ball at sea level.
However, a high altitude ball used at high altitude does not slow down as much through the air as a normal ball used at sea level. One way to slow it down through the air would be to make it lighter, but then it would be struck at a higher speed as it comes off the racquet. The only other alternative would be to make the ball slightly larger in order to increase the drag force on the ball. The drag force on the ball is proportional to ρR2, where R is the ball radius. If the density drops by 20%, then R2 would need to increase by 20% to compensate, so the ball diameter would need to increase by 10%, from 66 mm to 72.6 mm.

