ABSTRACT

The kick serve in tennis is difficult to master since it is difficult to generate enough topspin for the ball to kick up sharply. Furthermore, the ball needs to be served at around 100 mph (depending on the court surface — grass and clay being very different surfaces), and it needs to land well short of the service line in order to bounce to around shoulder height.  The main problem is that the racquet is near the top of its trajectory when it strikes the ball, so it is impossible to swing up at the ball at the same steep angle as that used in a topspin groundstroke. A high ball toss will help since a falling ball is equivalent to a rising racquet in terms of topspin generation. In addition, it helps to strike the ball with the racquet head tilted forward slightly. Additional topspin is generated simply by the fact that the racquet is rotating forward when it strikes the ball. The physics of each of these effects is described in this article, and is illustrated with slow motion video film showing both the serve action and the fact that the resulting spin is mostly sidespin in a typical kick serve.

1. INTRODUCTION

A kick serve is one that bounces up around shoulder height as it crosses the baseline. It also swings into or away from the receiver due to sidespin imparted to the ball. Not everyone can serve a good kick serve. The male pros all have a good kick serve, and so do some of the female pros. The secret of success is being able to serve with topspin (in addition to sidespin) and being able to serve fast. In general, the faster the ball lands in the court the higher it will bounce, but a fast serve on its own does not necessarily bounce to around shoulder height. A fast, flat first serve usually bounces to around waist height. In order to bounce to shoulder height, the ball must land at high speed and at a relatively steep angle.

Normally, the faster the serve, the lower the angle of incidence on the court since a ball served at high speed needs to pass low over the net in order to land in the serve box. But if the ball is served with topspin, the ball will dive onto the opponent's court at a relatively steep angle, even when serving at relatively high speed. An interesting question is how the serve speed, the angle of incidence of the ball onto the court and the amount of topspin can all be optimized to generate the highest possible trajectory as the ball crosses the baseline. In this article, I present some measurements and calculations to indicate how the bounce height can be increased. Measurements of kick serves were needed in order to figure out the physics of the problem, which turned out to be more complicated than expected.

One of the mysteries concerning the kick serve is how the server manages to generate topspin in the first place. In order to achieve a good kick serve, the racquet head needs to rise up the back of the ball, as it does in a topspin groundstroke. To return a groundstroke with topspin, players normally swing the racquet upwards at an angle of about 30 degrees to the horizontal. That way, an upwards friction force is exerted on the back of the ball, causing the ball to rotate with topspin if the racquet is swung fast enough. The incoming ball bounces off the court with topspin, so the spin direction needs to be reversed in order to return the ball with topspin. In a serve the racquet head is almost at the top of its trajectory when it strikes the ball, so the racquet is rising at an angle of only a few degrees just before it strikes the ball. Therein lies the mystery. If the racquet needs to rise at 30 degrees to hit a good topspin forehand, how can anyone serve a ball with a significant amount of topspin when the racquet head is rising at only a few degrees?

One saving grace is that the ball is not spinning backwards when it is struck, so the server does not need to apply as much spin in a kick serve as in a groundstroke. In effect, the same outgoing spin can be achieved with only about half the effort. Another significant factor is that the racquet is usually swung faster when serving a ball than when hitting a groundstroke. The outgoing spin is proportional to the speed of the racquet head, and is also proportional to the approach angle of the racquet head. The first two factors help to increase the amount of topspin in a kick serve, but there are several other factors that also add to the spin, as described in Section 2.

When serving a kick serve, right-handed players toss the ball over their left shoulder, arch their back, bend at the knees and then jump up off the court. The end result is that the racquet head strikes the ball in a direction that is partly sideways across the back of the ball and partly vertical up the back of the ball, as shown in Fig. 1. The sideways component generates sidespin and the vertical component generates topspin. In Fig. 1, the ball will have more sidespin than topspin since the horizontal speed of the racquet head is greater than the vertical speed. Sidespin causes the ball to curve from right to left through the air, as viewed by a right-handed server, or from left to right for a left-hander. Topspin causes the ball to curve down onto the court at rate that is faster than the effect of gravity alone.

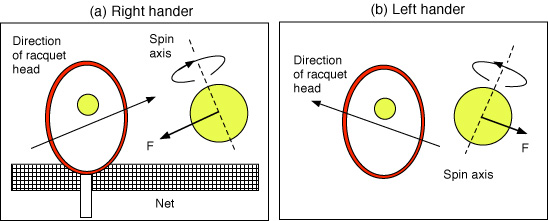
Figure 1 — Direction of racquet head and spin axis in a kick serve, as viewed by (a) a right hander and (b) a left hander. The ball is traveling into the page toward the net. The spin is primarily sidespin here with a small topspin component. The aerodynamic Magnus force, F, acts at right angles to the spin axis, pushing the ball down onto the court and causing it to curve to the left in (a) or to the right in (b). F is in the opposite direction to the friction force on the ball generated by string motion across the back of the ball.

2. SPIN GENERATION

The situation shown in Figure 1 is the one normally used to describe how players strike the ball in a kick serve, and it shows how sidespin is generated as well as topspin. That doesn't mean that the ball spins about two separate axes. There is only one spin axis and it is tilted away from the vertical. If the axis in Fig. 1 is vertical, then there is no topspin, just sidespin. If the axis is horizontal, then there is no sidespin, just topspin. If the axis is tilted, then any point on the ball will rotate in a circle around the axis, and it rotates simultaneously in vertical and horizontal directions.

Video film of a kick serve shows that the situation is more complicated than that shown in Fig. 1. There are several additional effects that need to be considered in order to understand what happens in a kick serve. The main effects are these:

1. Racquet Tilt. If the racquet head is tilted forward when the head strikes the ball, rather than being exactly vertical, then additional topspin is generated and the ball will pass lower over the net. The same effect occurs in a topspin groundstroke. The effect of racquet head tilt is shown in Fig. 2. Suppose that the head is tilted forward and approaches the ball in a horizontal direction at 80 mph, as in Fig. 2(a). The physics of the collision is exactly the same if the racquet is at rest and the ball approaches at 80 mph as in Fig. 2(b). That is what a bug would see if the bug was sitting at rest on the frame of the racquet. Since the ball approaches the racquet at an angle, it will bounce off the racquet at an angle with topspin. The same thing would happen if the ball bounced off the court at an angle. The result of the collision in Fig. 2(a) is that the ball is served in a downward direction with topspin, even if the racquet head is not rising when it strikes the ball.

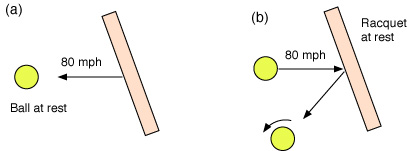
Figure 2 — (a) If a racquet approaches a ball at 80 mph with the head tilted forward, then the ball will be served with topspin even if the head is not rising. The same amount of spin is generated if the ball approaches the racquet at 80 mph and the racquet is initially at rest, as shown in (b).

2. Gyrospin. Some players tend to strike the ball slightly towards the side of the ball rather than exactly across the back of the ball, in which case the ball will also spin about a horizontal axis pointing towards the net. That sort of spin is used to throw a gridiron football, but it has no effect on curvature of the ball through the air.

3. Ball toss. If the ball is struck when the racquet is exactly vertical and is at its maximum height, then there is no vertical motion of the racquet head at all. Nevertheless, the ball will still be struck with topspin, and it will head downward towards the net rather than being served in a horizontal direction. Effects 3 , 4 and 5 can all lead to this result and they all result in additional topspin when the head is rising to meet the ball.

When the ball is struck, the ball is falling down towards the court as a result of the ball toss. If the ball falls down onto the racquet strings, then that is equivalent to the racquet head rising to meet the ball. The faster the head rises and the faster the ball falls, the more topspin is generated. If the head is rising and the ball is not falling then the ball will be struck in an upwards direction. If the head is not rising but the ball is falling, then the ball will be struck in a downwards direction. Normally, the head is rising and the ball is falling when the ball is struck, and the result is that the ball usually heads toward the net in a downward direction — partly because of the ball toss effect and partly because of effects 1, 4 and 5.

4. Downward force. The racquet head is rotating rapidly towards the net when the ball is struck. The racquet head rotates through an angle of about 10 degrees while the ball is on the strings. If the ball is struck when the head is vertical, then the ball will come off the strings when the head is tilted forward by about 10 degrees. The ball will come off the strings at an angle of about five degrees below the horizontal, rather than 10 degrees, since the force on the ball is a maximum half way through the impact, and is zero at the start and end of the impact. On average, the force on the ball acts in a direction about 5 degrees below the horizontal in that case. The serve angle also depends on the height of the ball toss and whether the head is rising when it strikes the ball. The serve angle is very important in a fast serve since an error of two degrees can result in a fault where the ball either hits the net or lands long.

5. Racquet Rotation. The strings grip the ball during a serve. If the racquet rotates 10 degrees while the ball is on the strings, then the ball also rotates 10 degrees, in the topspin direction. The same effect would occur if the ball was glued to the strings since the ball and the racquet would both rotate 10 degrees. The ball is not glued to the strings but it is squashed against the strings. The top end of the racquet is rotating faster than the bottom end, so the top side of the ball is pushed harder towards the net than the bottom side. As a result, the ball rotates with topspin, even if the racquet head is not rising when it strikes the ball. If the racquet head is indeed rising when the ball is struck, then the amount of topspin will increase. Ten degrees of forward rotation in 0.004 seconds corresponds to about 400 rpm of topspin, which is about the same as one gets when the racquet head is rising. In a kick serve, the ball spins at around 4000 rpm, but most of that is due to sidespin. The amount of topspin is typically less than 1000 rpm.

Figure 3 shows a simple model of the rotating racquet effect. The ball can be represented by a mass M plus two springs. If the racquet moves in a straight line towards the ball, both springs compress equally and the ball accelerates in a straight line without rotating. If the racquet is rotating then the top spring compresses more than the bottom spring so the force N1 is greater than N2 and the ball will rotate in the same direction as the racquet. If the racquet head is also rising, then the back of the ball grips the strings and rises with the racquet while the front tends to remain at rest, and this will generate additional topspin. If the ball is falling when it is struck, the back of the ball is gripped by the strings while the front keeps falling, adding to the amount of topspin.

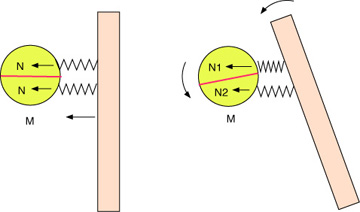
Figure 3 — A ball can be represented by a mass M and two springs. If the racquet rotates then so does the ball since the top spring will compress more than the bottom spring and will exert a greater force on the ball.

3. TYPICAL SERVE RESULTS

Video film showing a few kick serves can be seen below in Movie Screen 1. Film was taken at 300 fps (frames per second) looking side-on (along the baseline), then the camera was moved to view from the rear (looking along the center line). The camera was then moved back to the side-on position to film at 600 fps while zoomed in close to see the ball more clearly (Figure 4).

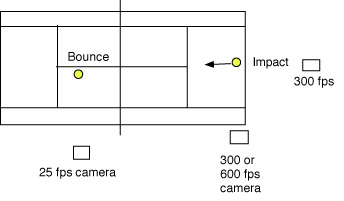
Figure 4 — Camera positions used to film kick serves.

The ball was marked with various dots, circles and lines so that both the spin rate and the spin axis could be determined. In addition, measurements were made from the video film of the speed and angle of the racquet head, as well as the speed and angle of the ball. A 25 fps camera was also positioned on the other side of the net to determine the landing position of the ball, as well as the incident and rebound speeds and angles. Eight players were selected from high ranked juniors coached by Tennis NSW, with an average age of about 20, and filmed in March 2011 during a regular coaching session.

4. INTERPRETATION OF SPIN

Measurement of spin rates from high speed video film is relatively easy. The spin axis remains fixed while the ball travels toward the net, so the time for one revolution can be measured in terms of the number of video frames required for a particular mark or pattern on the ball to re-appear in the same orientation. When filming at 600 fps, the mark re-appeared after about 8-10 frames or about 8/600 to 10/600 seconds, giving a spin rate of 60 to 75 revolutions/sec or 3600 rpm to 4500 rpm.

It is much more difficult to locate the spin axis, unless the spin axis happens to be exactly vertical or exactly horizontal. If the spin axis is vertical, then all marks on the ball rotate in a horizontal direction, and a horizontal line around the equator remains horizontal, as indicated in Fig. 5(a). If the spin axis is horizontal and points to the camera, then all marks on the ball rotate in a circular path around the middle of the ball. Otherwise, the marks and lines rotate in a manner that can be difficult to interpret. For example, Figs. 5(b) and (c) show two positions of the equator, one half revolution apart, when the axis is vertical and the equator line is inclined at an angle to the axis. It might appear that the ball is rotating with topspin, given the rotation of the equator line during half a revolution, but if the axis is vertical then there is no topspin at all. In that case, marks on the ball rotate purely in the horizontal direction and then disappear around the back of the ball.

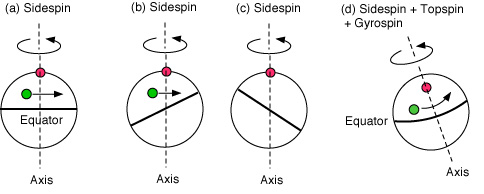
Figure 5 — Lines and marks on a ball can be used to determine the location of the spin axis. The red dot here marks the position where the axis passes through the surface of the ball.

Figure 5(d) shows a situation where the axis is perpendicular to the equator line but the top end of the axis is tilted to the left and is also tilted out of the page. In that case, the equator line appears stationary on video film, giving the false impression that there is no topspin. All marks on the ball rotate in circular paths around the axis, so the axis can be identified by the motion of those marks. If the axis is horizontal and pointing in the same direction as the motion of the ball, then the spin is classified as gyrospin. That type of spin is used when throwing an oval-shaped football. If the spin axis is essentially vertical but tilted in a direction toward the net in a serve, then the ball will have a small gyrospin component. If the spin axis is tilted sideways, in a direction parallel to the net or the baseline (as in Fig. 1) then the ball will have a small topspin component.

The approach used by the author to determine the spin axis was to mount a ball in such a way that its axis could be fixed in any given position, and then to rotate the ball about that axis in order to compare the result with the video film. A certain amount of trial and error was needed to identify the spin axis, but it was usually close to the orientation shown in Fig. 1. That is, the axis was usually tilted away from the vertical by about 10 or 20 degrees, although it was also tilted slightly toward the net in some cases, meaning that the ball was struck slightly toward the front of the ball rather than exactly at the rear of the ball.

5. ESTIMATION OF TOPSPIN

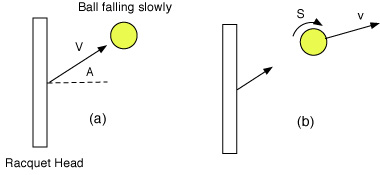
Figure 6 — (a) Racquet head approaches the ball at speed V and angle A. The ball is falling slowly. (b) The ball emerges at speed v and with topspin, at S rpm. In a kick serve, the angle A is only a few degrees, but is shown here as a relatively large angle for clarity.

The amount of topspin generated in a serve due to vertical motion of the racquet head can be estimated by considering the situation shown in Fig. 6. The racquet head is vertical and is approaching the ball rapidly at speed V and angle A, while the ball falls slowly. We can ignore sideways motion of the racquet head for the moment, in order to calculate the amount of topspin. Sideways motion is a separate issue and it generates sidespin, in the same way that vertical motion of the racquet head generates topspin. After the racquet head strikes the ball, the ball will emerge at speed v and with topspin, as indicated in Fig. 6(b). The ball emerges at high speed towards the net and it usually heads slightly downward toward the net. In Fig. 6(b), the ball is shown heading slightly upward since that is the effect of the upward friction force of the strings acting on the back of the ball. The friction force must act in an upward direction to generate topspin.

If the ball is struck when the strings are vertical, and if the head is moving in a horizontal direction without any rotation when it strikes the ball, then there will be no upward force on the ball. The only force on the ball in that case would be a horizontal force. There would be no change in the vertical speed of the ball, so the ball would continue to fall vertically at the same vertical speed it had just before it was struck. The ball would then head downward at a few degrees to the horizontal.

If the ball is struck when the strings are vertical, and if the racquet head is rising when it strikes the ball, then there is a vertical force on the ball that causes it to rotate with topspin and that reduces the speed at which the ball falls as a result of the ball toss. Furthermore, the racquet head tends to be inclined forward slightly when it strikes the ball, which generates an additional downward force on the ball. In that case, the whole diagram in Fig. 6 needs to be rotated slightly so that the racquet head is tilted forward and the ball emerges in a downward direction. In addition, the racquet head rotates a few degrees while the ball is still on the strings, which also helps to project the ball downward.

The amount of topspin is shown in Fig. 6 with the symbol S. Experiments and theoretical estimates both indicate that S is given to a good approximation by S = 1.45 VA where S is the spin in rpm, V is the racquet head speed in mph and A is the approach angle in degrees. For example, if A= 0 then S = 0 meaning that there is no spin generated at all. If V = 100 mph and A = 30 degrees then S = 4350 rpm. The amount of spin therefore increases with both the speed of the racquet head and the approach angle of the racquet head. The amount of spin also depends on the speed of the incoming ball, but in a serve, the ball is almost at rest when it is served.

Figure 6 also describes the result when the racquet is moving sideways across the back of the ball, and is approaching the ball at a sideways angle A. In that case, the ball acquires sidespin, and the amount of sidespin is given by the same expression S =1.45VA. In practice, the racquet head usually approaches the ball as shown in Fig. 1, with a large sideways approach angle and a relatively small vertical approach angle. As a result, the ball is usually served with about 4000 rpm of spin in a kick serve, but the spin is mostly sidespin and the amount of topspin is relatively small. That is, the spin axis is almost vertical, as indicated in Fig. 1.

In a typical kick serve, the racquet head approaches the ball at about 65 mph and rises at an angle of about 5° just before impacting the ball. The amount of topspin in that case is about S = 1.45 × 65 × 5 = 471 rpm. If the ball toss is not right, and the ball is struck a bit further forward, the vertical approach angle of the racquet head might be only one degree, then the amount of topspin will be five times smaller. If the ball is struck a bit earlier, the approach angle might be 10° instead of 5° then the amount of topspin will double. However, if the ball is struck too early, then it might land on the baseline instead of the service line. Hitting up at a greater approach angle to the ball generates more topspin, but the ball is then launched at a higher angle over the net.

6. SPIN DUE TO BALL TOSS

Suppose a racquet approaches a ball in a horizontal direction at speed V and the ball is falling vertically at speed v as shown in Fig. 7(a). We can work out the amount of topspin by supposing that the ball is at rest and the racquet is rising vertically at speed v while simultaneously moving horizontally at speed V, as shown in Fig. 7(b). The situation is then the same as that shown in Fig. 6 and the spin will be given by the same formula. If the ball falls say 3 feet before it is struck then it will be falling at 9.5 mph when it is struck. If it falls from a greater height it will be falling at a greater speed when it is struck. In a kick serve, V is typically about 65 mph if the ball is served at 90 mph. The racquet approaches the ball at an angle A given by tan A = v/V = 0.146 in this case, so A = 8.3°. That angle could well be larger than the actual vertical approach angle of the racquet in a typical kick serve, in which case the ball toss would account for more than half of the topspin generated. Using the formula S = 1.45VA, we find that S = 780 rpm due to the ball toss alone.

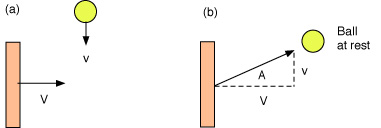
Figure 7 — (a) A racquet approaches a ball at speed V while the ball is falling at speed v. A bug on the ball sees the ball at rest while the racquet is rising at speed v, as shown in (b).

7. BALL TRAJECTORY AFTER BOUNCING

In the remainder of this article, I present some theoretical calculations of ball trajectories in a kick serve. The calculations are based on experimental observations, but it is easier to show the effects of varying ball spin, speed and angle by calculating the effects rather than by measuring them. The calculations are presented in two stages. First, we examine the ball trajectory after the ball bounces, since that is what determines the height of the ball as it crosses the baseline. Then we examine the whole trajectory from the serve point to the baseline to show how bounce height is affected by changes in the serve action.

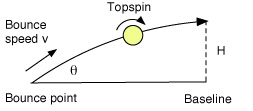
Figure 8 — The ball crosses the baseline at height H after bouncing up off the court at speed v and angle θ. In a kick serve, v is about 20 m/s, θ is about 20° and H is about 5 or 6 ft. The ball bounces with topspin, at about 600 rad/s (5730 rpm). The distance from the bounce point to the baseline is about 6 to 8 m (20 to 26 ft). The perpendicular distance from the net to the service line is 21 ft. The perpendicular distance from the service line to the baseline is 18 ft.

After the ball lands in the service box, it bounces up off the court at speed v, at an angle θ, with topspin ω, and then crosses the baseline at height H, as shown in Fig. 8. In general, the height H increases as v increases, it increases as θ increases, and it decreases as ω increases. Topspin causes the ball to dive down onto the court which is good if you want the ball to land at a steep angle in the service box and to kick up at a steep angle. After the ball bounces, the effect of topspin is to reduce the bounce height.

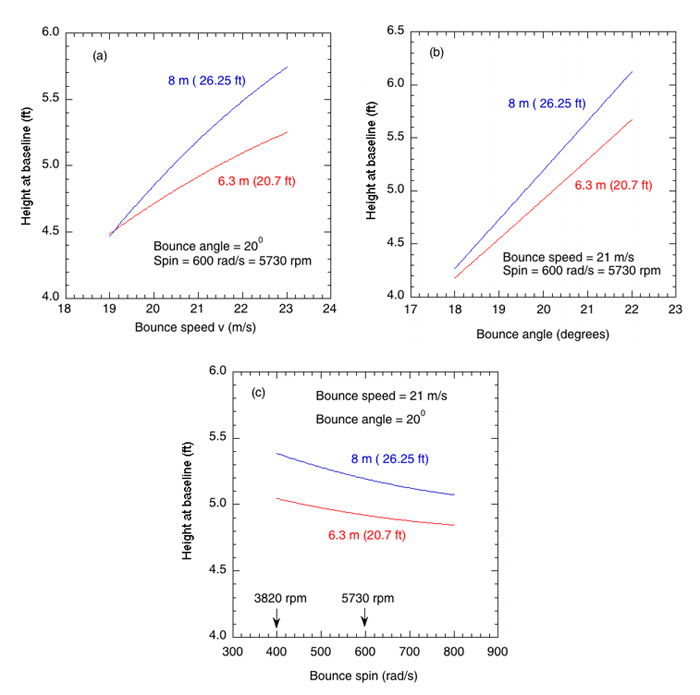
Figure 9 — Height of the ball as it crosses the baseline, either 6.3 m or 8.0 m from the bounce point.

Effects of varying these parameters are shown in Fig. 9, based on trajectory calculations that allow for aerodynamic lift and drag forces on the ball. Fig. 9(a) shows the effect of changing the bounce speed, assuming that the ball bounces at θ = 20° with 600 rad/s (5370 rpm) of topspin. The ball then travels a horizontal distance of either 6.3 m (20.7 ft) or 8.0 m before crossing the baseline. The shortest distance from the service line to the baseline is 5.49 m (18.0 ft). The ball needs to travel a longer distance to the baseline if it bounces before reaching the service line, especially when served wide rather than down the middle. Fig. 9(b) shows the effect of varying the bounce angle, and Fig. 9(c) shows the effect of varying the rebound spin of the ball. The ball speeds, spins and angles shown in Fig. 9 are all typical of those in a kick serve. Fast, flat serves bounce off the court at an angle of about 14°.

The bounce speed and angle both have a big effect on the bounce height. The higher the bounce angle the better, and the higher the bounce speed the better. The distance to the baseline is also important, given that the ball is still rising as it crosses the baseline in most of the cases in Fig. 9. If the ball bounces well short of the serve line then it has further to travel to the baseline so it will cross the baseline at a greater height. The ball always bounces with topspin. The amount of topspin after the bounce increases with serve speed and with the angle of incidence onto the court, but the amount of topspin does not have as strong an effect on the bounce height as the bounce speed or angle.

It is clear from these calculations that a good kick serve is one where the ball bounces off the court at a large angle and at high speed, especially if the ball lands in the service box well short of the baseline. An alternative method of getting the ball to bounce over the receiver's head is available at low serve speeds, although no one ever uses this method. Figure 10 shows the height of the ball as it crosses the baseline, for low bounce speeds and high bounce angles. These results could be obtained by serving underarm or overarm so the ball falls from a large height into the service box and bounces to a large height. Alternatively, the ball could be smashed or volleyed at low speed into the service court to bounce in this manner. In order to calculate the results in Fig. 10 it was assumed that the ball spin changes with bounce speed and angle in such a way that the ball bounces in a rolling mode, as it normally does when incident on the court at a large angle of incidence.

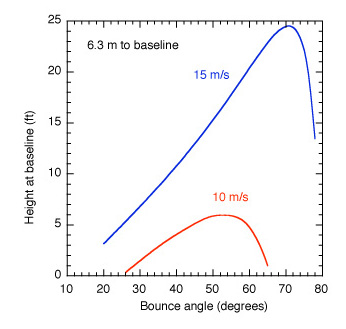
Figure 10 — Height of the ball as it crosses the baseline, either 6.3 m or 8.0 m from the bounce point.

8. SERVE PARAMETERS

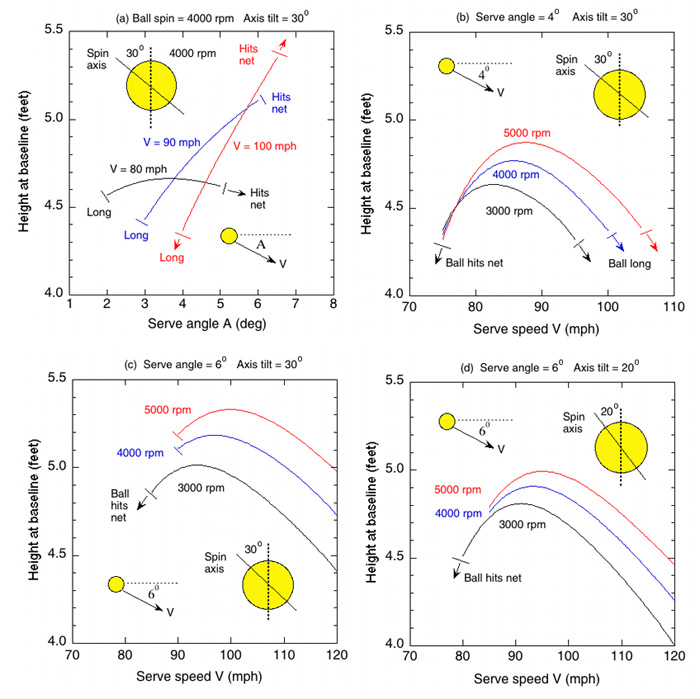
Figure 11 — Height of the ball as it crosses the baseline, vs serve angle A in (a) and serve speed V in (b), (c) and (d). The angle A is the serve angle in degrees below the horizontal. The ball spin is either 3000, 4000 or 5000 rpm, as labeled, and the spin axis is tilted at either 20° or 30°, as labelled. A larger tilt angle means more topspin. If the serve angle is too small or the serve speed is too high, the ball will land long (beyond the serve line). If the serve angle is too large or the serve speed is too low, the ball will not clear the net. It was assumed that the ball is served down the center line for these calculations.

In order to get the ball to bounce up off the court at high speed and at a large angle, the ball must normally be served at high speed and with topspin. Calculations for a range of serve speeds, serve spins and serve angles are shown in Fig. 11. The spin values shown in Fig. 11 refer to the amount of spin generated as the ball comes off the racquet, not the spin after the ball bounces off the court. Despite the fact that the server swings up at the ball in a kick serve, the ball must be projected downward below the horizontal for a good serve. The serve angle, A, is typically between 2 and 6 degrees below the horizontal. It was assumed in Fig. 11 that the ball is served down the center line when deciding whether the ball hit the net or was long, and when calculating the height of the ball as it crossed the baseline.

The height of a ball served at 80, 90 or 100 mph as it crosses the baseline is shown as a function of the serve angle in Fig. 11(a), assuming that the ball is spinning at 4000 rpm and the spin axis is tilted 30° from the vertical. It is clear from this diagram, and the other results in Fig. 11, that the ball needs to be served at a speed greater than 80 mph for a good kick serve. At 80 mph, the ball bounces to a height of just over 4.5 feet, regardless of the spin and serve angle. The highest bounces occur when the ball is served at about 90 to 100 mph and at about 6° below the horizontal so the ball just clears the net.

Figure 11(b) shows the bounce height at the baseline vs serve speed when A = 4°, for three different values of ball spin. The bounce height increases with spin, but it does not necessarily increase with serve speed. At high serve speeds the ball lands closer to the serve line, assuming the serve angle is fixed at 4°, so the angle of incidence is low and the ball bounces at a low angle. In order to increase the bounce height, the ball needs to be served at a steeper angle, as shown in Fig. 11(c). However, if the amount of topspin is reduced then the ball will again land close to the service line and the bounce height is reduced, as shown in Fig. 11(d).

Several assumptions were made in calculating the results shown in Fig. 11. The distance between the two baselines is 78 feet, but the distance between the server and the point at which the ball crosses the opposite baseline can be greater than 78 feet, especially when serving wide. To calculate the results in Fig. 11 it was assumed that the ball is served down the center line. In that case, the relevant distance to the opposite baseline is 78 ft. Larger bounce heights can be obtained by serving wide rather than down the center line. The ball was served from a height of 2.9 m (9.5 ft), starting 0.6 m (2 ft) in front of the server's baseline. To calculate the change in ball speed when the ball bounced, it was assumed that the vertical speed after the bounce was 0.8 x the vertical speed before the bounce (i.e., COR = 0.8), and it was assumed that the horizontal speed, v_x2, after the bounce was 0.65 x the horizontal speed before the bounce. The calculations were slightly simplified by assuming that the ball bounces in a rolling mode, with v_x2 = Rω₂, where R is the ball radius and ω₂ is the angular velocity of the ball (in rad/s) after it bounces. The bounce parameters here are typical values, chosen from experimental data.

The specific parameters used to calculate the results in Fig. 11 are of less significance than the general trends, which show that the bounce height at the baseline increases with the amount of topspin imparted by the server, and it also increases as the serve angle, A, increases. Serving downward at a relatively large angle has two main advantages. It means that the angle of incidence on the court will be large, so the bounce angle will be large. It also means that the ball lands well before the service line, so the ball has a longer distance to travel before it crosses the baseline. At moderately high bounce speeds, the ball rises all the way 15 to the baseline, so the longer travel distance allows the ball to rise to a greater height by the time it reaches the baseline. The advantage of serving with topspin is that the ball is incident on the court at an even steeper angle and at a greater vertical speed than a ball served without topspin.

9. GENERATION OF TOPSPIN

It is interesting to consider how topspin is generated when viewed from the perspective of a moving ball striking a stationary racquet. Even though the ball is almost at rest when it is struck in a serve, it is useful to consider the serve in a reference frame where the racquet is at rest just before the impact with the ball. If a racquet is swung at 80 mph at a stationary ball, a bug sitting on the racquet strings might think it was at rest and the ball was approaching at 80 mph, as shown in Fig. 12(b).

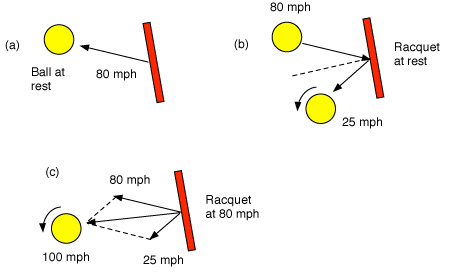
Figure 12 —A racquet approaching a ball at 80 mph, as in (a), can be viewed as if the ball approaches the racquet at 80 mph, as in (b). The ball will bounce off the racquet at about 25 mph, but in the court frame of reference (c) the ball is served at about 100 mph.

A ball incident on a stationary racquet at 80 mph will bounce off the racquet at about 25 mph and with topspin. Viewed in the court frame of reference, as in (c), the ball is served at about 100 mph. The actual speed, spin and angle of the served ball depends on the approach angle of the racquet, the tilt angle of the racquet head and the speed of approach of the racquet head. If the racquet head was vertical at impact and approached the ball in a horizontal direction, then the ball would be served in a horizontal direction without any topspin. In order to increase the amount of topspin, the angle of incidence of the ball onto the strings, as shown in Fig. 12(b), needs to be increased, a result that can be achieved by tilting the racquet head forward and by increasing the approach angle of the racquet head. Tilting the racquet head forward, as indicated in Fig. 12, also has the effect of projecting the ball down below the horizontal.

10. TOPSPIN VS SIDESPIN

Suppose that a ball is spinning at 4000 rpm and the spin axis is tilted 30° away from the vertical. The spin of the ball is completely specified by these numbers, but does it make sense to say that the ball has say 3000 rpm of sidespin and 1000 rpm of topspin? Can we add the separate spins in this way to calculate the total spin?

In order to calculate the results in Fig. 11, I did not separate the spin into topspin and sidespin in order to calculate the force on the ball. Rather, I worked out the Magnus force (F in Fig. 1) from the "total" spin and then calculated the vertical component of that force, F_V, knowing the tilt angle. If F_M is the Magnus force on the ball and θ is the tilt angle, and if the ball is traveling in the horizontal direction, then F_V = F_M sinθ. For example, if the spin axis is tilted by 30° then F_V = 0.5F_M so the vertical force on the ball due to spin is half the total force. The horizontal force due to the ball spin is given by F_M cos θ = 0.87F_M. The sideways force on the ball is reduced only slightly when the spin axis is tilted by 30° but the vertical force increases by a relatively large amount. The two forces don't simply add up in the usual way to give the total force since forces add as vectors.

Similarly, the two spin components don't add up in the usual way to give the total spin. Nevertheless, spin can be regarded as a vector with magnitude and direction and can be regarded as having vertical and horizontal components or separate sidespin and topspin components. But it is difficult to then calculate the Magnus force on the ball from the two separate components, the problem being that the aerodynamic force on the ball depends on the total spin of the ball, not just the topspin or the sidespin component. The vertical force on the ball cannot be calculated just from the topspin component. The amount of sidespin also needs to be taken into account.

11. ANSWERS TO QUESTIONS

Q: Can a kick serve be hit slower than 80 mph?
A: Yes. The graphs above in Figure 11 refer specifically to the height of the ball as it crosses the baseline when the ball is served down the center line. In most cases, the ball is still climbing as it crosses the baseline, so the eventual height of the ball might exceed 6 ft. It is also possible to serve a topspin lob at low speeds with a high bounce, as shown in Figure 13 below, but the ball then drops sharply as it crosses the baseline. Even higher bounces can be expected on clay courts since the ball slows down more in the horizontal direction and therefore kicks up at a steeper angle.

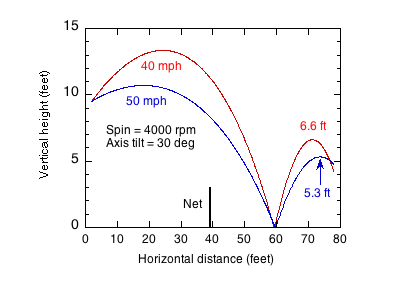
Figure 13 — Low Speed, High Top Spin 'Lob Kick Serve'. The ball leaves the racquet at an upward angle, bounces high, but then drops sharply as it crosses the baseline.

Q: Does the ball toss really contribute to spin?
A: Yes. Movie Screen 2 demonstrates this. The pendulum in the videos is an upside-down version of a serve — a rising ball in the video is equivalent to a falling ball in a serve. As the videos show, in a serve, if the ball toss is falling, topspin is created. If the ball is rising, underspin is the result. If the ball is stationary at its peak, then there is no spin. These results are for a horizontally moving pendulum (racquet). The pendulum speed is too slow and rotation contact too small (1-2 degrees) in these videos to demonstrate the racquet rotation effect discussed in Section 2.