1. ABSTRACT

The specific question answered by this research is whether there is a difference in rebound spin for impacts at, above, and below the long axis of the racquet. Additionally, the experiment examined whether adding substantial amounts of weight to the periphery of the racquet head at 3 and 9 and 1 and 11 o'clock would influence the rebound spin at each of the three impact locations. It was found that impacts below the axis produce more topspin but that adding sufficient mass at 3 and 9 o'clock on the racquet head could reverse the maximum spin location. It was further found that adding mass to the racquet periphery will increase topspin at all locations, though more at some than others. The practical consequence of this investigation is that a player might be able to effectively optimize or maximize topspin production with the appropriate customization of the racquet for his customary impact point.

2. THE EXPERIMENT

A Prince EXO3 Red 105 racquet was strung with Tourna Big Hitter Blue, 16 gauge, polyester string at 55 lbs. This racquet was chosen because the large "string ports" on the periphery of the frame allowed easy addition of weights by bolting 100 gram lab weights to the 3 and 9 o'clock and 1 and 11 o'clock positions as shown in Figure 1. Such large weights are not realistic for actual customization and play but were used to magnify the effect and to guarantee measurable results. Enough weight was added to guarantee that results were mass related and not due to variances in incident angle, speed or spin or from an inherent randomness to individual rebounds.

Figure 1 — Racquet with 100-gram weights bolted to 3 and 9 o'clock of the racquet through large "string ports" featured on this racquet.

Balls were fired with a ball machine at an average of 48 mph (22 m/s) at a 24-degree angle to the racquet face perpendicular with backspin of 2900 rpm (307 rad/s), as shown in Figure 2. The racquet was stationary and suspended in such a way that it could twist, rotate and translate about all three dimensional axes. The handle suspension device had a mass of about 300 grams. The mass of a hand can be between 300 and 600 grams depending on the size of the player.

Figure 2 — Impact angle of 24 degrees, backspin to the strings (topspin to court frame of reference) of 3000 rpm (315 rad/s) and speed of 48 mph (22 m/s).

The actual impact parameters would vary slightly due to small variances in the delivery of the ball machine. These impact variances were as follows: speed = 22 m/s +/- 1 m/s; angle = 24 degrees +/- 1.5 degrees; spin = 2900 rpm +/- 300 rpm. Because spin is sensitive to changes in these three parameters, the results were normalized to the average values of each parameter. In that way individual impacts could be reliably compared to each other. The technique of normalization is explained in Which Strings Generate the Most Spin?.

The ball was aimed at three locations about 22 inches from the butt and 2 inches above and below the long axis, as well as on the axis, as shown in Figure 3.

Figure 3 — Impact location 22 inches from the handle butt and 2 inches above and below the long axis.

Three sets of experiments were performed. First, spin was measured for impacts on the racquet without weights attached. Second, impacts were made after the weights were bolted to the racquet at 3 and 9 o'clock. Third, impacts were made after the weights were bolted to the racquet at 1 and 11 o'clock. Data was then measured and compared for the three locations with and without the weights.

3. RESULTS

Racquet Without Weight. Upon an informal survey at Tennis Warehouse, most players guessed that if there were a difference in spin due to impact location that high impacts would produce more spin. The intuitive bias and explanation was simply that there is more room for the racquet to brush up behind the ball.

The results were just the opposite. As Figure 4 shows, for the racquet without additional weights attached, impacts below the longitudinal axis produce more topspin than impacts in the middle or above the axis. In fact, low impacts had an average of 53% more topspin than high impacts. This result was astonishing enough that the experiment was performed four separate times using slightly different setups, but with the same results each time.

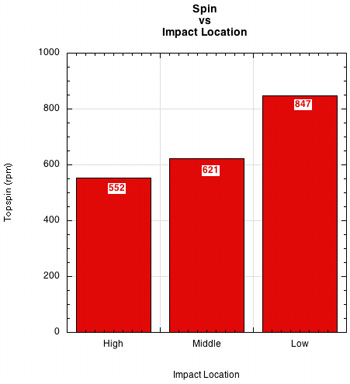
Figure 4 — Rebound topspin at high, middle and low impact locations without any peripheral masses added to the racquet.

These results are explained in the "Analysis and Discussion" section below.

Racquet With Weight at 3 and 9 o'clock. Adding 100 grams at both 3 and 9 o'clock provided some surprises. Figure 5 shows that adding weight increased the spin at all impact locations and that the impact location with the most spin was reversed. The high impact location produced 26% more spin than the low impact location.

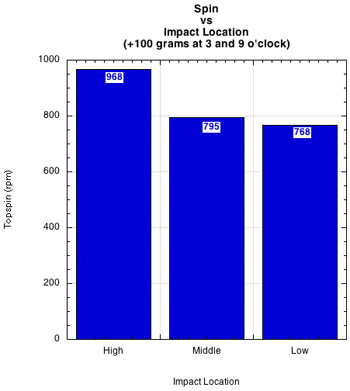
Figure 5 — Rebound topspin at high, middle and low impact locations with peripheral 100-gram masses added to the racquet at 3 and 9 o'clock.

Racquet With Weight at 1 and 11 o'clock. Changing the weight location to 1 and 11 o'clock produced results that were more similar with the racquet without weights. The low impact had 35% more spin than the high impact, as shown in Figure 6. There was more spin at all locations with extra weight than without.

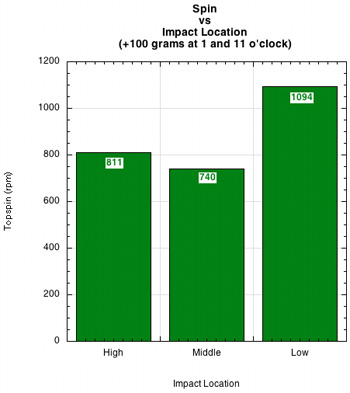
Figure 6 — Rebound topspin at high, middle and low impact locations with peripheral 100 gram masses added to the racquet at 1 and 11 o'clock towards the tip.

Combined Results. Figure 7 shows the graph of the combined results.

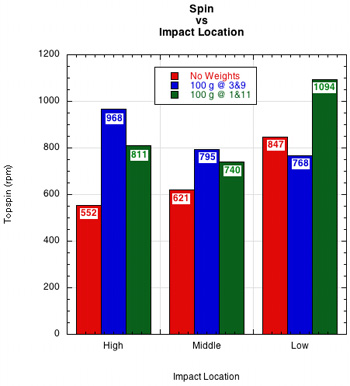
Figure 7 — Rebound topspin at high, middle and low impact locations with and without peripheral 100 gram masses added to the racquet.

In light of this data, three main questions need to be answered: How does impact location affect spin, why does increasing weight increase spin at all impact locations, and why does the maximum spin location depend on the location of the additional mass?

4. STRING AND RACQUET EFFECTS INFLUENCING SPIN

The above results are not easy to explain. There are 6 main stringbed effects that can influence spin on off-center hits for a given racquet, string, and tension:

• Short-side Effect (also known as 'drum effect')
• Rotation Effect
• Friction Effect
• Bending Effect
• String Movement Effect
• Weight Effect

It will be helpful to first explain these effects, and then we can analyze how each effect may vary and influence spin depending on impact and mass location.

Short-side Effect. On off-center impacts the strings will stretch and deflect backwards. The section of string between the ball and the frame closest to the ball will deflect the same amount as the longer side, but it will stretch a greater percentage of its length than the longer side. This makes this section of string stiffer, increase more in impact tension, and form a steeper 'rebound wall' than the long side. Figure 8 illustrates this.

Figure 8 — The short-side deflection shown on the left (or top) for the mains is also occurring for the crosses at the top, as shown on the right (or bottom). For such an impact, not counting for other factors discussed below, the short-side string will exert a topspin torque on the top half of the ball (as viewed in the photo at left (top)).

The strings that we are most interested in are the cross-strings. The short-side cross string will exert a greater force on its side of the ball than will the longer segment, and it will do so at an angle more biased toward the center of the strings.

On impacts above the longitudinal axis, the short side will exert its force in the topspin direction on the backside of the ball. Below the axis, it will exert its force in the backspin direction. This is demonstrated in Movie Screen 1. In this movie a ball is dropped on an array of strings acting as cross strings (left to right in the movie). There are no mains in the setup. The ball is incident at 90 degrees with no spin. The short-side force creates a clockwise spin and an oblique rebound angle to the right. The opposite will happen if the ball is dropped onto the right short side — the ball will angle toward the left and spin counter-clockwise. In other words, one side will produce topspin and the other will produce backspin.

Movie Screen 1 shows the stringbed in a clamped condition. There is no recoil or rotation of the stringbed upon impact. This clamped condition accentuates the short-side effect. Adding sufficient mass to the 3 and 9 o'clock periphery of the racquet head will also approximate the clamped condition, reducing rotation and increasing topspin on high impacts and decreasing it on low impacts. Similarly, removing such weights increases the rotation effect and will act to lessen or even reverse the short-side effect.

Rotation Effect. When the ball strikes above the longitudinal axis, the impact point will rotate backwards around the axis (experienced as twisting in one's hand). When it strikes below the axis it will rotate in the opposite direction. Impacts directly on the axis will cause no such rotation.

On a high impact the racquet periphery rotates away from the top of the ball and the center moves toward and under the bottom half of the ball touching the strings. On a low impact the racquet center rotates into and over the top half of the ball and the periphery moves away from the bottom half of the ball. This has a number of consequences.

First, as shown in Figure 9, there will be more eccentric force where the racquet is rotating into the ball and less where it is rotating away. Thus, on a high impact with no weights attached, there is more force of the bottom left quadrant, as shown by the more compressed spring. This will diminish topspin. On a low impact, there is more force on the top left quadrant, increasing topspin.

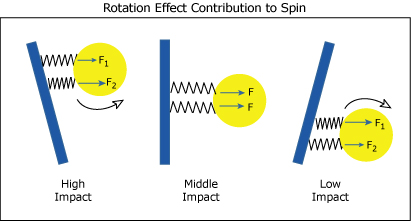
Figure 9 — As the racquet rotates, it moves away from one quadrant of the ball (reducing the force between ball and racquet) and into the adjacent quadrant on the string side of the ball (increasing the force). Impacts close to the middle (there are no exact middle impacts because the ball slides across the stringbed when incident at an oblique angle) will exert very little torque.

Second, this effect is the opposite of the short-side effect. Thus, the net force on the ball due to these two effects will depend on the exact location of the impact and the amount and location of mass we attach to the periphery.

Third, as discussed in regard to the string movement effect below, the rotation will either position the laterally deflected main strings into or away from the ball, respectively increasing or decreasing the efficiency of the topspin producing snap-back of those strings.

Fourth, the rotation during impact changes the effective angle of impact. On a high impact, the top of the racquet rotates backward, turning the racquet into the ball's direction and effectively decreasing the angle of impact. The opposite happens on low impacts, thus effectively increasing the angle of incidence. This leads to the friction effect discussed below.

Friction Effect. Increasing the angle of incidence (as measured from the normal [perpendicular] line to the stringbed) increases topspin, and decreasing the angle decreases topspin. An increased angle increases the relative speed of the strings to the ball and friction must therefore do more work to reverse the incoming spin before the ball will bite (where the speed of the spin is equal to the speed of the ball across the strings — see article on String Snap-back and Spin for more information on biting and the role of friction in spin production). The friction effect is demonstrated in Movie Screen 2. A ball incident to a hand-held racquet at right angles and no spin rebounds with spin.

In the movie, as the racquet rotates the ball slides across the strings toward the frame. Friction resists this motion by pushing in the opposite direction, creating a clockwise torque that spins the ball. In this example, the initial relative speed of the ball to the strings in a direction parallel to the strings is zero. When the racquet rotates and the ball begins to slide, the impact angle is effectively increased. By the time the ball leaves, the racquet may rotate about 5 degrees, though the average angle for the entire impact might be between 2-3 degrees. Movie Screen 2 shows the rotation and friction effects as being greater than the short-side effect, otherwise the ball would be spinning in the opposite direction or not spinning at all, if the two effects were equal.

Movie Screen 3 presents an example of the short-side effect being greater than the friction effect. Here there is no racquet rotation because the racquet is clamped, but the racquet is oriented at a slight angle to the incoming ball in such a manner that it should exert a counter-clockwise spin due to friction resisting the slide to the left and creating a torque on the bottom of the ball. However, in this case, the short-side torque is greater than the friction effect torque and the net result is a small clockwise spin.

Bending Effect. Movie Screens 4 and 5 shows why we might be interested in bending. When weight is attached at 3 and 9 o'clock, there is a very obvious distortion of the frame (the weight serves to slow the vibration frequency and increase the amplitude so we can more easily see it on video). This distortion appears to be happening in several directions at once.

Similar bending could also be seen on the racquet without weights and the racquet with weights at 1 and 11 o'clock. But the 3 and 9 o'clock racquet makes it most obvious. Figure 10 isolates the first five frames of the impact to better able to see the bending.

Figure 10 — Still images from Movie Screen 4 to compare frame bending during and immediately after impact.

We have to be careful when interpreting object distortions and rotations when using high-speed video. First, it is difficult to discern whether you are seeing bending, folding, twisting, rotation or a combination. The bending mode is the largest and slowest type of bending, and is the easiest mode to identify. Secondly, most cameras introduce a distortion inherent in the way they either mechanically or programmatically expose the photo. This effect is known as the rolling shutter effect. That means that the camera starts exposing at the top and moves down the frame, successively exposing each row of pixels. If the object is moving very rapidly to the right, as in the video, then the top of the racquet will be exposed first and then, after the racquet has travelled to the right, the bottom of the racquet exposed, thus skewing, stretching, bending the racquet to the right. Sometimes the distortion might be in the direction that is actually occurring or it might be in the opposite direction. This effect is especially pronounced if you have a long object that fills the vertical space of the frame.

To substantially correct for this, the camera must be turned sideways to the motion. That was done for these videos. In Movie Screen 4, the camera is exposing from the right to the left. Because the racquet is very thin in that direction, there will be very little bending distortion due to the camera (at least for the type of bends we are looking at). The distortion that might take place instead would be compression in the direction of motion, but the racquet is so thin that this is very difficult to observe, nor is it relevant to the bending that interests us.

When the racquet bends in any direction it will initiate repetitive vibrations of a basic bending pattern. Depending on the direction of the bend, these vibrations can be between 120 and 600 Hz (cycles per second). The key to any influence upon spin would be the net direction and magnitude of the torque on the ball caused by the motion and orientation of the bending movement. Thus the timing, direction, and magnitude of the bend while the ball is in contact with the strings are important.

The frame can bend and twist in several directions. Figure 11 displays the bending modes that might affect topspin. For convenience, we will refer to these as bending, folding and twisting.

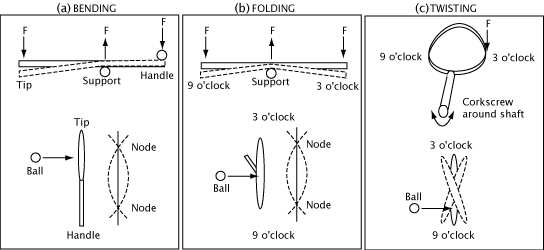
Figure 11 — (a)Bending: the bending mode transverse to the long axis and the one most usually referred to when speaking of shock and vibration. (b) Folding of the head between 3 and 9 o'clock about the long axis. (c) Corkscrew twisting of racquet head around long axis through the shaft.

The frame will distort and then vibrate in any given direction depending on the stiffness and mass. Vibration is measured as the number of cycles (frequency) of back and forth that occur in one second. One cycle per second is 1 Hz. Bending as in Figure 11a occurs between 100 and 200 Hz. Folding as in Figure 11b occurs at 5-700 Hz. Vibration frequency increases with increasing stiffness and decreasing mass, and it decreases with decreasing stiffness and increasing mass. The vibration amplitude (the maximum displacement of a point on the frame during each back and forth) increases with increasing mass and decreasing stiffness and decreases with increasing stiffness and decreasing mass. For example, the frequency of the bending mode (Fig. 11a) for the three racquet setups was as follows: racquet with no weight = 133 Hz, weights at 3 and 9 = 118 Hz, and weights at 1 and 11 = 111 Hz.

For each vibration type, there are points along the racquet known as nodes. These are points that do not vibrate. They act as stationary points around which the racquet bends. If the ball impacts at a node, the racquet will not vibrate. The further the ball impacts from the node, the larger the amplitude of the vibration, though the frequency remains the same. If the ball impacts between two nodes, the racquet bend at the impact point will be concave; if it hits above or below the two nodes, the racquet bend at the impact point will be convex. The concavity or convexity can make a difference to spin in the folding mode (Figure 11b) (and it can add sidespin in the bending mode).

There are other racquet deformations that occur also. The frame can exhibit what is known as hoop vibration in which the racquet head alternately expands and contracts horizontally and vertically or where the frame twists back and forth around its circumference. These will not affect spin however.

Adding weights to the racquet periphery can change the location of the nodes, moving them closer to the added masses. In the extreme case, if enough weight is added, the weight location can effectively become a node. A fun video demonstrating this is presented in Movie Screen 6. Here the nodes appear to be just a bit to either side of the central mass.

String Movement Effect. When the ball impacts the string it deflects perpendicular to the stringbed and, usually, 1-3 individual strings displace laterally. The ball is incident with backspin (topspin in the court frame of reference) and usually at a descending angle (which is determined by both the speed and angle of the ball and the speed, swing angle, and head tilt of the racquet). As the ball strikes the strings, the backspin initially produces a larger force on the side of the ball that is rotating into the strings. This helps to move those strings laterally. As the ball slides across the stringbed and spin is reversed and the ball slowed, there is a greater force at the ball's leading edge to its travel across the strings. By then, however, the force pressing the strings together is too great to move these leading-side strings much, if any. Therefore, most of the string movement, both in terms of quantity and magnitude, takes place on the trailing-edge half of the ball. This can be seen in Figure 12.

Figure 12 — Strings under the trailing-edge to the ball's movement (arrows) are the ones that move laterally in the stringbed.

Under the best circumstances the laterally displaced strings will snap back, applying a topspin torque to the ball. However, as we will examine below, the impact location and mass distribution will affect the efficiency of energy transfer of the snap-back.

Weight Effect. Adding weight to a racquet will increase both its swingweight and twistweight. The amount of increase will depend on the distance of the weight from the axis of rotation. For swingweight the axis is usually taken either about the butt end or 4 inches from the butt, perpendicular to the handle and parallel to the string plane. Twistweight is measured about the long axis. Increasing swingweight will reduce rotation of the racquet about the swingweight axis and increasing twistweight will decrease rotation (twisting) around the long axis. Increased mass will also decrease the recoil (translation) of the center of mass backward. The result is a greater impact force, more string deflection, more ball flattening, longer dwell time, and slower bending with greater amplitude for impacts between the weights. In this experiment, increasing twistweight is of greater concern for spin production because it has greater influence on the other effects discussed above. Increasing twistweight decreases the influence of the rotation and friction effects and increases the influence of the short-side and bending effects. It also increases the string movement effect by increasing the time, area, and force of action. It is for this latter reason that there was more spin in all impacts with the weighted racquets compared to the no-weight impacts. This is especially true for impacts in the middle. Here there is no short-side, rotation, or preferential bending direction effects. String movement is the only effect left to influence spin.

5. ANALYSIS AND DISCUSSION

Spin will depend on the net contribution of all the effects discussed above. The contribution of each effect to topspin varies depending on impact location and distribution of the added masses. Figures 13, 14, and 15 display typical impact sequences for each of the impact location and weight distribution scenarios. Each sequence demonstrates the racquet rotation and frame bending of each impact condition.

High Impacts.

Figure 13 — High Impacts. Impacts above the long axis for a racquet with no added weights, weights at 1 and 11 o'clock, and weights at 3 and 9 o'clock.

No weight added: The rotation effect dominates. As the top of the racquet rotates, short-side force is lessened (reducing topspin), laterally moved strings move away from ball (reducing topspin), impact angle and relative ball speed effectively reduced and with it the work done by friction (reducing topspin). Bending not visually conclusive, but perhaps the top of the frame bends backward, effectively adding to the rotation effect. Racquet rotates under ball exerting torque that reduces topspin.

Weight at 3 and 9 o'clock: Weight increases impact force, increases ball and string deformation, moves folding mode vibration nodes toward 3 and 9 o'clock increasing concavity of bend, reduces vibration frequency and increases bending amplitude, increases dwell time, reduces rotation and accentuates short-side effect. Friction effect is diminished because of very little clockwise rotation. All these events contribute to topspin.

Weight at 1 and 11 o'clock: The effect is somewhere in between the no-weight racquet and the 3 and 9 o'clock racquet. All the anti-topspin effects of the no-weight condition are present, but to a much lesser degree, and the topspin favorable effects for high impact (short-side and bending effects) are less diminished. Throw in the favorable weight effects on string movement and you get more topspin than without weights, but less than weights at 3 and 9 o'clock.

Low Impacts.

Figure 14 — Low Impacts. Impacts below the long axis for a racquet with no added weights, weights at 1 and 11 o'clock, and weights at 3 and 9 o'clock.

No weight added: Rotation effect dominates. The bottom of the frame rotates away from the leading edge of the ball increasing the angle of impact and rotating the racquet and laterally deflected strings into the trailing half of the ball, creating topspin. Short-side effect is reduced by counter-clockwise rotation and bending is negligible.

Weight at 3 and 9 o'clock: Rotation is greatly reduced, and the torque is dominated by the short-side and bending effect. Spin is increased compared to the no-weight racquet because of the weight and string movement effects, but not as much as for high impacts with weight at 3 and 9 o'clock.

Weight at 1 and 11 o'clock: Reduced but still favorable rotation, friction, and bending effects plus weight and string movement effects all combine to increase topspin.

Middle Impacts.

Figure 15 — Middle Impacts. Impacts on the long axis for a racquet with no added weights, weights at 1 and 11 o'clock, and weights at 3 and 9 o'clock.

No matter the weight location, all short-side, rotation, and bending effects are non-existent and weight and string movement effects combine to determine spin. The spin is approximately the same for both weight-location conditions and, in both cases, more than the no-weight condition.

6. CONCLUSION

High and low impacts are mirror reflections of each other. Whatever increases topspin on the one will decrease it on the other. With normally weighted racquets, low impacts will produce more spin than high impacts that are an equal distance from the long axis. Impacts in the middle will have topspin somewhere between the two. These results can be reversed by adding enough weight far enough away from the long axis. Adding weight increases the location dependent short-side and bending effects and decreases the rotation and friction effects. Adding weight will increase the string movement effects in all locations. The weights added in this experiment were more that a player would ever add in reality. However, if the effects of adding weight are linearly dependent on the amount of weight added, then it can be assumed that the effect on spin seen in this experiment can be generalized and scaled accordingly. That being the case, a player might be able to improve spin performance by customizing racquets with lead weight. In any case, this study helps us better understand some of the variables and complexities involved in spin production.