ABSTRACT
The Physics of Adding Weight To Customize Tennis Racquets
Double pendulum simulations of a racquet swing were performed. The pendulum translated and rotated in a single horizontal plane activated by a constant energy input generated by a mass dropping from a specified height. Various masses were added at multiple locations along the "racquet" section of the double pendulum. Motion was analyzed by use of high speed video. The relationships of racquet and ball speed to quantity and location of added mass were analyzed. The influence of mass distribution on swingweight, hittingweight (effective mass), power potential (coefficient of restitution), "plow-through", "whip-through", impact angle, and control are also discussed.
I. INTRODUCTION
Why Players Weight-Customize Tennis Racquets
The relationships between racquet weight, balance (center of mass — CM), swingweight (moment of inertia — I), swing speed and shot speed are often topics of much confusion among tennis players. Questions arise such as, "How can a heavier racquet swing easier than a light racquet?"; "How can a head-heavy racquet have a lower swingweight than a headlight racquet?"; "Does making a racquet more headlight increase its racquet tip velocity?"; Is it true that adding weight at the axis of rotation has no affect on the swingweight and thus the racquet speed?"; "Does more mass create more plow-through?"; "Does a heavier racquet create more ball speed?"; "Is there a trade-off between racquet mass, racquet speed, and ball speed?". We will examine these and other questions regarding the performance effects of varying a racquet's mass distribution. Our primary interest is what effect does the addition and redistribution of mass have on racquet speed, control, feel and ball speed. We will discuss many of the factors that influence these in order to fully understand the role of mass distribution in racquet performance.
This study was prompted first by the fact that racquet customization using lead tape has become very popular and second by two common statements made by players that did not make sense from a physics point of view. Those statements are that adding weight to the butt made the racquet swing faster and adding weight to the tip made the racquet "whip" through, also implying faster and more powerful. Belief in such statements would obviously affect one's customization strategies, perhaps resulting in loading up both the butt and tip with lead tape. That, indeed, is a common strategy, though its benefits may be manifest in areas other than the expressed purpose of the customization.
Whenever a large percentage of players say something is happening, then it probably is, even if it is not exactly what they say it is in their description and even if they don't agree what it is. The vocabulary of perception and experience often obscures the physical event itself. The words "heavy," "light," "head heavy," "head light," "plow-through," or "whip-through" create preconceptions that shape a player's perceptions and explanations (and a researcher's). To get to what is really happening, a simple experiment must be devised to break the event down to its bare bones.
In this case, a double pendulum device was created to model a tennis stoke. The double pendulum concept has been used more extensively to describe golf strokes [Jorgensen, 1] but less so for tennis. Rod Cross has pioneered the concept in tennis [2, 3] and baseball [4].
An actual tennis stoke is a very complicated behavior involving motion and rotation of numerous joints, appendages and the racquet in three dimensions. But the basic physics is the application of forces in such a way to move and rotate the racquet to a desired destination and velocity. The double pendulum allows us to examine the results of these forces in a manageable manner. We are not concerned with the actual mechanics of the shoulder, forearm and wrist during a swing, nor do we care how or why a player is exerting a force on a particular segment. Once the force is applied, the racquet will move depending on the quantity and distribution of both its mass as well as that of the body segment applying the force. In that way, we can determine whether more or less mass located at any location will increase or decrease racquet and ball speed. It does not matter whether the player is using an Eastern or a Western grip or has a flat or window wiper swing. Once the force is applied to the racquet, the amount and distribution of mass will determine the racquet's motion. One grip type might indeed swing a racquet faster, but that is due to the application of larger forces due to the mechanics of the resulting swing, not due to the distribution of mass.
This latter fact is key to the following experiment. Many factors in a tennis swing can contribute to causing a larger or smaller force being applied to the racquet. In order to compare the effects of changing mass distribution, we must keep the applied force the same. More precisely, we will keep the input energy the same. Rod Cross [5] has shown that more force is automatically generated by swinging or throwing a more massive object, so all we can really do is control the energy that is applied to the swing.
II. THE EXPERIMENT
THE SETUP
Double Pendulum. A Double Pendulum was constructed using a pull-induced force to swing the "forearm" and "racquet" in a plane horizontal to the ground (Figures 1-3). The forearm was a hollow aluminum beam 54.5 cm in length with a mass of 840 grams, including all additions such as springs, stops, axis bolts, and two 200 gram masses used to make the forearm much heavier than the racquet. The racquet was a solid wood beam 65 cm in length with a mass of 117 g. A forearm and hand together weigh about 2.5-5 lbs (1136-2270 g), depending on the person's weight. That is 4-8 times greater than that of a typical 300 g racquet. The forearm in this experiment varies between about 3-7 times as much as the racquet, depending on the masses added to the racquet, so the relative weights are approximately correct. The forearm rotated around an axis at a fixed hinge at its end ("forearm axis"). The racquet rotated about a "wrist" axis 2.5 cm from its butt end (Figure 2).
The force to swing the pendulum was created by dropping a 7.5 lb weight connected by Kevlar string to the forearm. The weight dropped in free fall for 140 mm whereupon it became taut and exerted a force on the forearm. The weight then fell another 72 mm, pulling the forearm until just prior to ball impact (Figure 1). The swing-initiating energy remained constant throughout the experiments. This was a critical parameter of the experiment. The idea was to see how swing speed and ball speed changed with changes in racquet mass and distribution of mass for a given input energy. A player can always react to changes in mass and distribution by swinging faster or slower and thinking the result is caused by the mass variations and not the extra swing effort, which can be so minimal as to not be perceived. A tennis ball was placed at the approximate location of maximum racquet speed and its speed was measured after impact.
Masses of 20, 50, 75, 100 and 200 grams were placed at prescribed locations along the racquet — typically at 10, 20, 30, 40, 50, and 60 cm. These masses are much greater than most mass customizations a player would attempt, but they were chosen to make sure unmistakable results were obtained that could only be accounted for by the difference in the masses. Three to five impacts were performed for each mass/location combination. Linear and angular velocities were measured for both the forearm and the racquet at the CM, tip, butt, and impact point. Ball speed was also measured.
The entire apparatus is shown in Figure 1 and the racquet and forearm components are shown from the top and side respectively in Figures 2 and 3. Movie Screen 1 is a video of a typical swing of the device.
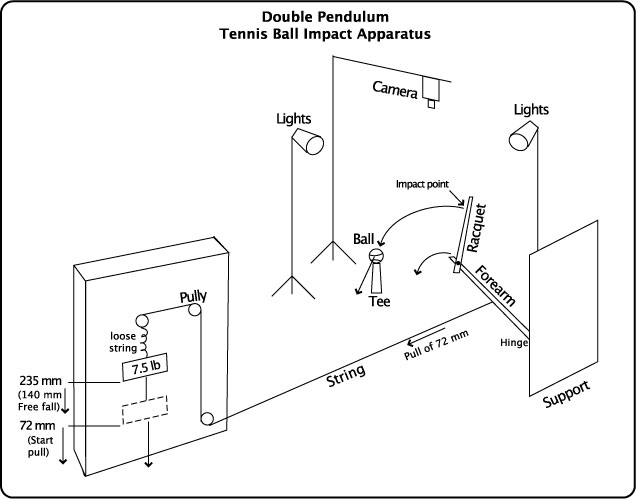
Figure 1 — Double Pendulum Apparatus.
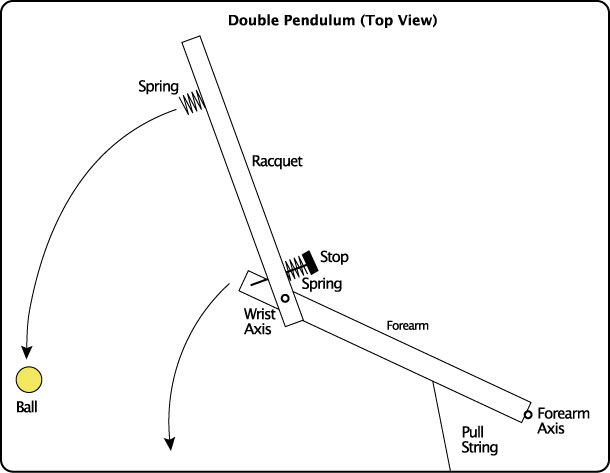
Figure 2 — Racquet and forearm components (top view). It's not obvious in the diagram, but the wrist spring and stop are connected to the end of the forearm, so the racquet would compress into the spring and the resulting torque would rotate the racquet forward.
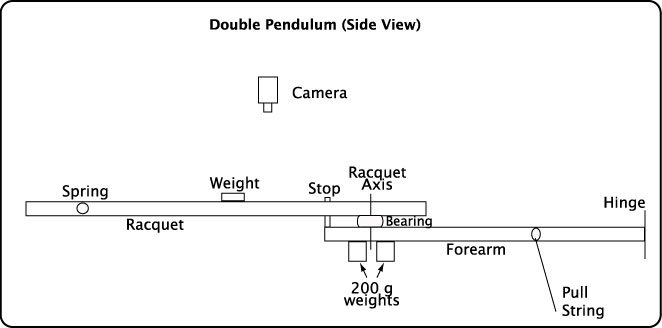
Figure 3 — Racquet and forearm components (side view). The various weights were placed along the racquet at 10 cm increments from 10 to 60 cm.
Movie Screen 1 shows the double pendulum hitting the ball.
Video 1
Double Pendulum Ball Hit
Movie Screen 1 — Double pendulum ball strike. The ball was placed at the approximate x-y coordinates of maximum racquet velocity. You can see the angle brace and spring used to restrain backward motion and to add a forward rotating torque. Also visible is the impact spring modeling the strings. A 50 g mass is visible at 60 cm from the handle end of the racquet. The pull string loses tension when the forearm is about vertical.
Note on movies: It is sometimes easier to see high speed movies by advancing one frame at a time using the right or left arrows on the keyboard or by scrolling the movie progress bar.
III. RESULTS
Players use racquet weight and balance as predictors of performance — racquet speed and ball speed. Over the years these have served players well, especially since the range of these parameters is very small for most racquets being used by most of the players. Swingweight is more of a nonintuitive concept, so many players pay it no attention because anything measured as a kg x cm2 has little intuitive meaning. The results below use swingweight calculated about the butt end of the racquet. This is different than the commonly used swingweight calculated about an axis of rotation located 4 inches from the end. This latter is an arbitrary and senseless location dictated solely by the mechanical logistics of the machines used to measure swingweight. A racquet cannot be rotated around that axis in a normal tennis stroke. Further, the effect on the player of adding mass on either side of the 4-inch axis is misrepresented. Swingweight increases as mass is added further from an axis. If the axis is at the end, "further" is always further. But if the axis is at 4", then mass added at 6" is the same distance from the axis as mass added at 2". This means the player would feel it equally difficult to swing each racquet. But, in reality, since one really swings from a minimum of the end of the racquet (approximately the wrist axis), the mass added at 6" will be more difficult to swing. Further discussion of swingweight and the choice of axis of rotation is presented in the Section 11 of the Results.
1. Racquet Speed
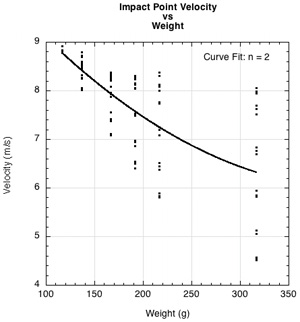
How does adding different quantities of mass at any location along the racquet affect racquet speed? It is obvious from Figure 4a that of the usual methods employed by players — weight, balance, and swingweight — swingweight is by far the most predictive parameter for answering this question. There is a great deal of scatter about the curve fit line for the mass (4b) and balance (4c) graphs, whereas there is very little on the swingweight graph. Consequently, if you know the swingweight of two racquets, you will know which will swing faster. Such a statement cannot confidently be made if all you know is weight and balance. Racquets with the same weight can swing radically different (Fig. 4b), and racquets with the same balance also can swing at different speeds (Fig. 4c).
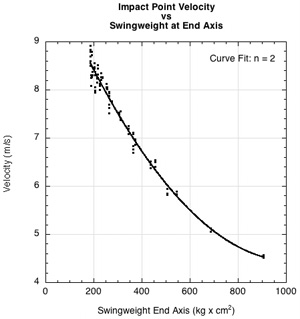
(b)
 (c)
(c) 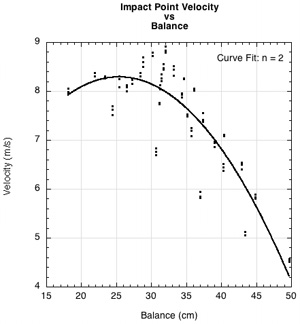
Figure 4 — Racquet velocity vs swingweight at end axis (a), vs mass (b), and vs balance (c)
It is apparent from Figure 4 that for a given input energy, racquet speed depends on swingweight and much less on mass or balance separately. Swingweight combines the effects of the amount and location of mass into one measurement and is thus a much better predictor of racquet behavior.
There is some hidden detail in the graphs of Figure 4. If we take the same graphs and highlight the data points according to the quantity of mass being added and its location, some additional information emerges (Figure 5).
(b)
 (c)
(c) 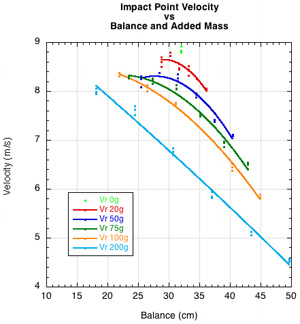
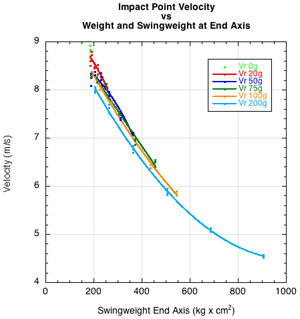
Figure 5 — Parameter comparisons for predicting racquet velocity. (a) Racquet velocity vs swingweight at end axis and mass added; (b) racquet velocity vs mass and location; (c) racquet velocity vs balance and mass added. For each mass represented by the colored curve fits, each data point moving to the right is a 10 cm increment in placement location along the racquet.
Figure 5 shows more specifically that for a given swing input energy, increasing mass at any one location will decrease racquet speed (Fig. 5b), and for any given mass, placing it further from the axis of rotation decreases racquet speed (Fig. 5c). Most importantly, at any given swingweight (Fig. 5a), heavier racquets will swing a slight bit slower than lighter ones — perhaps not even enough to perceive on court, but a measurable amount nonetheless. This is due to the fact that a swing, though mostly circular, is also part linear, so both weight and swingweight affect racquet speed.
The conclusion is that if the only thing you care about is racquet speed, then the rule of thumb is obvious: Add the least amount of mass as close to the rotation axis as possible, or, in other words, don't do anything.
2. Ball Speed
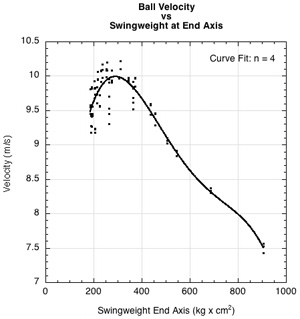
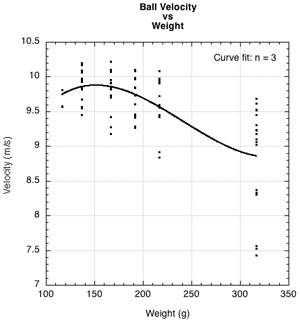
But racquet speed is not all that you want. Racquet speed is simply a means to an end — ball speed (and spin and maneuverability, which are not included in this study). Is swingweight, weight, or balance the best predictor of ball speed, and does adding mass increase ball speed even though it decreases racquet speed? The answers are provided in Figures 6-8 which display the side by side comparisons of the gross and detailed data fits for swingweight (Fig. 6), weight (Fig. 7) and balance (Fig. 8).
 (b)
(b) 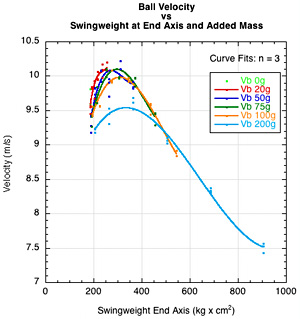
Figure 6 — Gross (a) and detailed (b) graphs of ball velocity vs swingweight at end axis.
 (b)
(b) 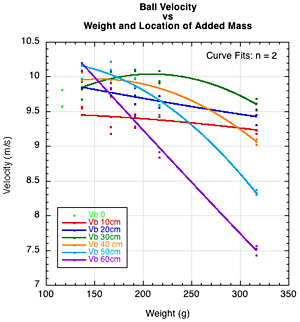
Figure 7 — Gross (a) and detailed (b) graphs of all ball velocity vs weight.
 (b)
(b)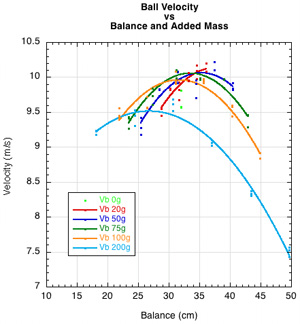
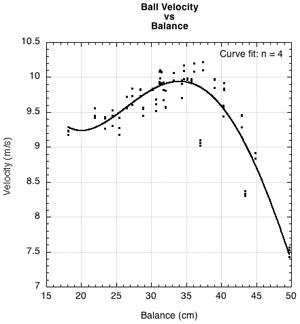
Figure 8 — Gross (a) and detailed (b) graphs of ball velocity vs balance.
As with racquet speed, swingweight is the best predictor of ball speed. For a constant energy input, ball speed increases at lower swingweights, peaks, and then decreases at higher swingweights. This makes ball speed prediction more complicated than that for racquet speed, which in turn makes a player's customization strategies more complicated. Ball speed depends both on racquet speed and power potential (ACOR), which depends on the hittingweight (effective mass) at the impact point, which depends on swingweight. Ball speed is a balancing act: for a given input swing energy, does increasing the power potential make up for the decline in racquet speed? To answer this, we must first delve deeper into the concept of power potential.
3. Power Potential (ACOR), Hittingweight (Effective Weight), and Bounce Speed
Power Potential. Power Potential is the industry term for apparent coefficient of restitution x 100 (ACOR, or eA in the equations below). ACOR is determined from the bounce of a ball off a handheld or free-standing racquet. Under that circumstance, ACOR is the ratio of the ball speed out (Vb2) to the ball speed in (Vb1):
eA = Vb2 / Vb1, (Equation 1a)
or
Vb2 = eA(Vb1) (Equation 1b)
In this case, the ball speed out is called the "bounce speed," and the ball speed in the "impact speed." The bounce speed depends entirely on the properties of the racquet, not the motion of the racquet. The speed of the bounce will depend on the location of the impact on the stringbed. The speed will be greatest in the throat area close to the CM, and gradually diminish as the impact moves towards the tip and/or outward to the periphery of the stringbed.
It can be shown [6] that the speed of a struck ball by a moving racquet depends on the ACOR of the stationary racquet:
Vb2 = eA(Vb1 + Vr1) + Vr1 (Equation 2)
where Vb2 is the ball speed out, Vb1 is the ball speed in, and Vr1 is the racquet speed before collision. The term in parentheses, (Vb1 + Vr1), is the impact speed, which in this case is the relative speed of the the ball and the racquet to each other. As such, it is the same as if the ball in were travelling this speed and the racquet was stationary, or vice versa.
For the above reasons, ACOR converted to a percent is called the "power potential" of the racquet. If you know eA from having done the bounce test, then you can just plug it into the equation to get the final ball speed. If, on the other hand, as in our experiment, you don't know ACOR but you can measure both ball and racquet speed before and after impact, then you can calculate ACOR.
Solving for ACOR,
eA = (Vb2 - Vr1) / (Vb1 + Vr1) (Equation 3)
You will notice that this description of ACOR is different than our free-standing racquet definition of ACOR, where the racquet is stationary at impact. In our experiment, it is the other way around: the ball is stationary and the racquet is moving. We can change the frame of reference by subtracting the racquet speed from both the before and after conditions: i.e., Vb2 = Vb2 - Vr1 and Vb1 = Vb1 + Vr1, which is what the equation states. And in the experiment, Vb1 = 0, so
eA = (Vb2 - Vr1) / Vr1 (Equation 4)
The sum of the ball and racquet speeds before the collision is known as the impact speed. It is the relative speed of each to the other. So, Equation 2 says that final ball speed is equal to ACOR times the impact speed plus the initial racquet speed.
Shot speed = ACOR(Impact speed) + Racquet speed
Bounce Speed. ACOR times impact speed is the bounce speed. This is the same as with the stationary racquet above, but bounce speed in the context of both the ball and racquet moving at impact is a bit more abstract. Bounce speed is not the same as shot speed, as it is for a stationary racquet. In the more general case, the bounce speed is the speed of the ball relative to the racquet. The ball bounces from the moving racquet, so the bounce speed is the shot speed (Vb2) minus the racquet speed at the impact point (Vr1). The best way to visualize this is for a ball hitting a stationary racquet. In this case the bounce speed is the shot speed. But what if the racquet is moving? If the racquet is moving 10 mph, the bounce will occur from a racquet already moving 10 mph. In this case, the ball starts at 10 mph before it even bounces. The bounce speed is then added on top of the racquet speed to achieve the shot speed. For each impact location on each racquet, the bounce speed is always a fixed percentage of the impact speed. (Tennis Warehouse has measured this for every racquet in 15 locations.) This percentage is known as the power potential (ACOR x 100). The bounce speed is the racquet's contribution to the shot. The impact location speed is the swing's (player's) contribution to the shot. So Equation 2 in words becomes:
Shot speed = Bounce speed + Racquet speed
This relationship is shown in Figure 9 for all the mass combinations in this experiment.
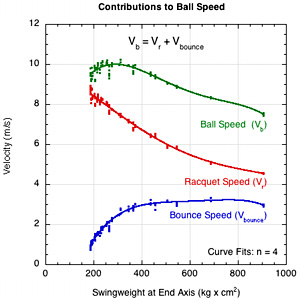
Figure 9 — The components of ball speed — bounce speed plus racquet speed in equals shot speed.
Hittingweight. Bounce speed is determined by ACOR, and ACOR is determined primarily by the local hittingweight, and much less so by frame stiffness, and stringbed stiffness. Hittingweight is the "effective" weight (or effective mass, Me) of the racquet at the impact location. The equation for hittingweight can be shown [7] to be:
1/Me = (1 / M) + (b2 / I) + (R2 / Iy) (Equation 5)
where, Me is the hittingweight, M is the mass of the racquet, b is the distance from the impact point to an axis through the balance point perpendicular to the racquet, I is the swingweight about the center of mass, R is the distance side-to-side of longitudinal axis of the impact point, and Iy is the twistweight (swingweight about the long axis).
The entire racquet weight is not involved when you hit the ball. Only the "local" weight is involved. The impact location behaves as if it were a localized mass. The racquet behaves (how much its motion is altered upon impact) heaviest at the balance point and lightest toward the tip and the periphery of the stringbed. The hittingweight is calculated using the location coordinates (distance of impact from the center line and from the balance point), swingweight, and twistweight (swingweight, or moment of inertia, about longitudinal axis). (Hittingweights for all racquets can be seen here.) The higher the hittingweight, the higher the racquet's power potential at the impact location.
These relationships are shown in Figure 10.
 (b)
(b) 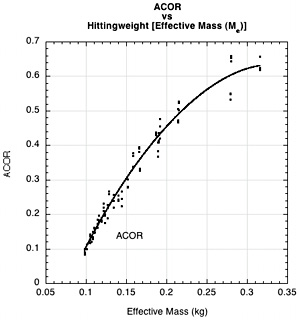
(c)
 (d)
(d) 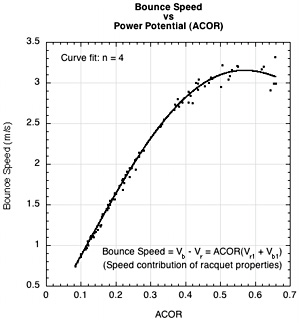
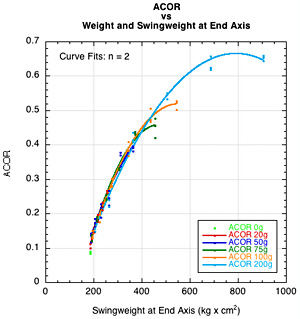
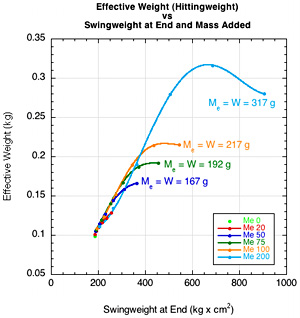
Figure 10 — (a) Power Potential (ACOR) vs Swingweight at end and added mass; (b) ACOR vs Hittingweight (effective mass, Me); (c) effective weight vs swingweight; and (d) bounce speed vs ACOR.
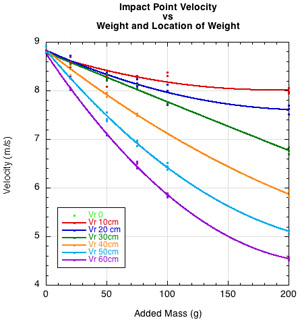
It is clear from Figure 10a and 10b that power potential (ACOR x 100) increases as swingweight and hittingweight are increased due to adding or appropriately redistributing mass. For a particular amount of added mass, it only increases up to a point however (as shown by the curling of each colored data fit in Fig. 10c). The reason is that the maximum possible value of hittingweight is the actual weight of the racquet. Only for impact at the balance point (CM) of the racquet will hittingweight equal actual weight. At all other impact locations above or below the balance point, hittingweight will be less, and when hittingweight is less, power potential is less. Figures 10a and 10c show ACOR and hittingweight peaking as the added mass brings the balance point closer and closer to the impact point.
The swingweight will always increase as you move a given added mass further from the axis, but the effective hittingweight and power potential will increase and decline on either side of the balance point (Figure 11). So you have situations as in Figure 10a where the swingweight is increasing but the power potential is decreasing. Hittingweight is defined in terms of the impact point's distance from the balance point. Maximum hittingweight is achieved if the impact location is the same as the balance point. The balance point of most racquets is well below the usual impact point. On the double pendulum, it is possible to adjust the balance point to unrealistic locations.
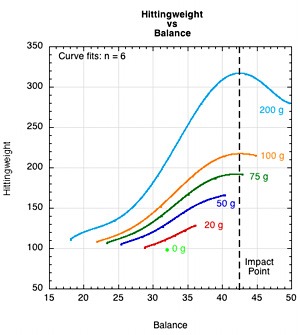
Figure 11 — The maximum hittingweight is equal to the total weight at the balance point. If impact is at the balance point, then maximum power potential will be achieved. For these experiments, the impact point was at the same location every time — 42.5 cm from the end of the racquet. When very large masses were added to the racquet, the balance point approached the impact point and even went past it, as seen for the 100 and 200 g curves.
4. Plow-Through
"Plow-through" is a term used by players to describe the feeling of a solid hit with little shock or vibration, with the perceived result of greater ball velocity. It is the degree to which the racquet wins the collision with the ball, maintaining as much of its pre-impact velocity as possible. In an effort to quantify this commonly used terminology, "plow-through" has been defined as a term of art as the percentage of post-impact racquet speed to pre-impact speed (measured at the impact location):
Plow-through = 100 x (Vr2 / Vr1)
Figure 12 shows that as swingweight is increased, plow-through is increased.
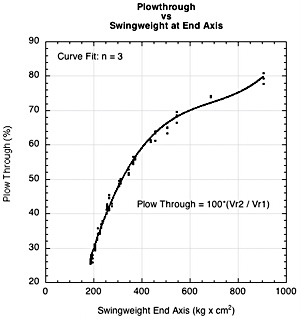
Figure 12 — Plow through. Plow-through is the percentage of the post-impact racquet speed to the pre-impact speed.
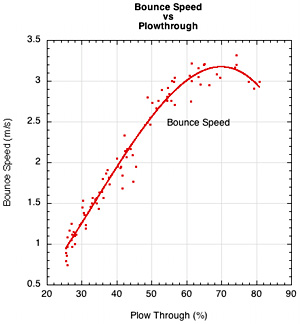
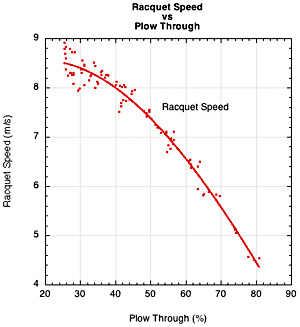
Plow-through is often associated with "crushing" the ball, which implies, in part, more ball speed. Figure 13 shows that as plow-through increases, bounce speed increases, racquet speed decreases and ball speed first increases and then decreases. This is all to be expected since plow-through depends on hittingweight and swingweight.
 (b)
(b)
(c)
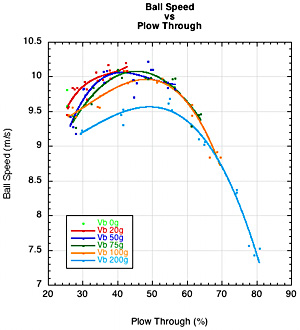
Figure 13 — Plow-through relationships. (a) Bounce speed vs plow-through, (b) racquet speed vs plow-through, (c) ball speed vs plow-through.
5. Control
Varying the amount and location of added mass affects the swingweight which in turn affects the relative speeds of the forearm and racquet. As a result, the angle at which the racquet will make contact with the ball at a fixed impact location will vary. This, of course, affects the direction of the ball's trajectory. Figure 14 shows how the hitting angle varies with increase in swingweight for a fixed energy swing and the ball located at a fixed location.
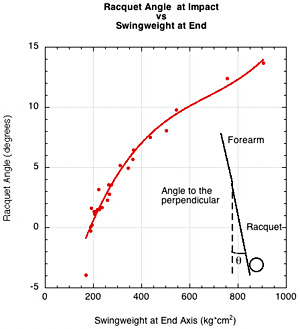
Figure 14 — Hitting Angle. Racquet angle to the ball at impact will affect the direction of the ball.
Figure 15 shows images of the racquet at impact for the two extreme cases in the experiment: no added mass (a) and 200 g added at 60 cm (b). Counter-intuitively for the greater swingweight case, the racquet hits as if impact were further "in front" or as if the racquet had swung through too soon. The forearm has swung through a smaller angle and the racquet through a larger one. The appearance is "out front" when compared to the forearm and the shot will be flying off at an angle to the horizontal. The appearance of hitting "early" is commonly associated with swinging too fast. However, the racquet is actually late to this impact location, having taken 1-2 ms longer longer than the no added mass racquet. Thus, if the ball were moving toward the racquet, unless the swing were begun earlier, the actual contact would have been made "late". But because the racquet is ahead of the forearm throughout much of the swing with the heavier racquet, the late impact might not lead to a shank.
 (b)
(b) 
Figure 15 — Impact Angles. Racquet and forearm angles at impact for the extreme conditions of no added mass (a) and 200 g at 60 cm (b).
6. Whip-Through
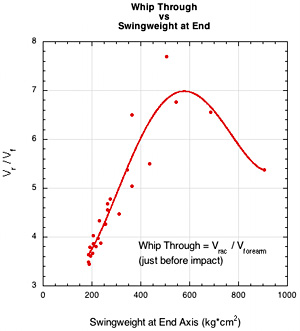
This sensation at higher swingweights of the racquet leading the forearm at impact is often referred to as whip-through. This refers to a player's perception that the racquet is effortlessly pulling itself through the swing, "whipping through" the ball. This whip-through feels both solid and fast due to high plow-through and impact out front. However, we know from the previous discussion that the racquet is indeed swinging slower at higher swingweight. The hypothesis that follows from this is that the sensation of a speedier, more powerful whip through is due to the relative speeds of the forearm and the racquet. As swingweight increases, the speed of the racquet increases relative to that of the forearm. As another term of art, we will call this ratio of racquet speed to forearm speed just before impact as "whip-through":
Whip-through = Vr1 / VFA1
Figure 16 shows that as swingweight increases, whip-through increases (up to a point) and the angle of the racquet to the forearm increases.
 (b)
(b) 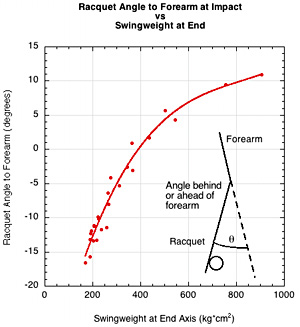
Figure 16 — Whip-Through. (Left) Whip-through at impact is the ratio of racquet velocity and forearm velocity. (Right) Racquet angle in relation to forearm: the angle ahead or behind of racquet to forearm.
The connection of whip-through to the player's sensation of increased racquet speed and ease of swing is speculative at this stage and has not been tested beyond this experiment. On court, the player does not have the luxury of a stationary ball, though he is often trying to make contact in "stationary" location relative to his body. The timing of the initiation of the stroke is crucial on court where it is not in the experiment.
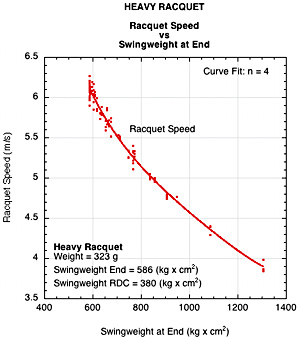
7. Heavy Racquet Comparison
As a check on the results, the experiment was repeated with a racquet almost 3 times as heavy as the one described above. The weight was 323 g, RDC swingweight of 380 kg x cm2, balance of 37 cm. The results are presented in Figure 17. The graphs essentially begin where the 117 gram racquet left off. With the heavy racquet, no matter where the mass was placed, both the racquet and ball speed decrease in every case.
 (b)
(b) 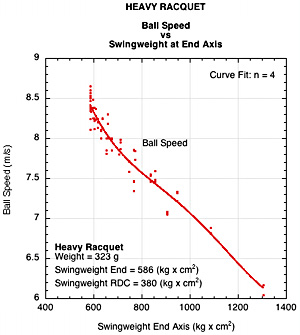
Figure 17 — Heavy Racquet Comparison. (a) Racquet speed vs swingweight at end. (b) Ball speed vs swingweight at end.
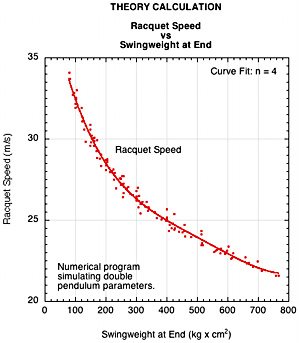
8. Numerical Theory Comparison
Rod Cross volunteered use of his double pendulum program to compare the experimental results to theoretical calculations. The program used larger racquet and ball speeds but still came close to qualitatively duplicating the the experimental data. The input conditions were different, but the results were close enough to show that experiment and theory were in agreement. Figure 18 displays the results of those calculations. The results confirm that racquet speed declines whenever and wherever you add mass to a racquet and that ball speed increases at low swingweight, peaks, and then decreases as swingweight increases.
 (b)
(b) 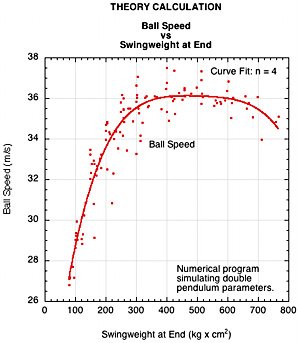
Figure 18 — Theory Comparison. (a) Racquet speed vs swingweight at end. (b) Ball speed vs swingweight at end.
9. Biomechanical Sequence
The theory behind the behavior of a double pendulum has been well documented by Rod Cross [2, 3] and others. Generally, the forearm reaches peak velocity first, then slows. As it slows, it pulls back on the butt end of the racquet, which accelerates the rotation of the racquet. Typically, as the forearm approaches or reaches its minimum velocity, the racquet achieves its maximum velocity. The maximum net swing velocity usually coincides with the maximum racquet velocity about the wrist axis of rotation. Figure 19 shows the forearm, racquet (at impact point), and swing velocities for two racquet setups: 200g at 60 cm and 50 g at 30 cm.
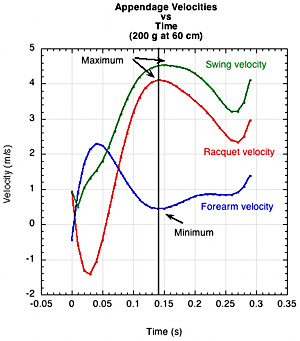 (b)
(b) 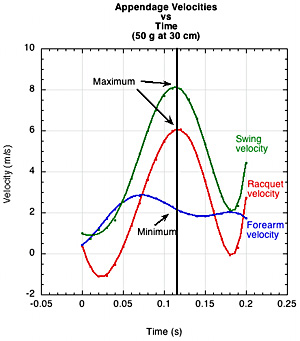
Figure 19 — Comparative appendage speeds. (a) Velocities for 200 g added at 60 cm (b) Velocities for 50 g added at 30 cm.
The graphs in Figure 19 might be prettier than for all actual tennis swings. A player theoretically can vary the force to the arm or racquet at any time. For example, a player could possibly accelerate the forearm throughout the stroke. This would have consequences to the hit, but its possibility does not allow us to anoint this "maximum-minimum" relationship to a law of the tennis forehand. Further research is needed.
10. Force
Rod Cross [5] reported that for maximum effort throwing of various mass balls, the force exerted on the ball automatically increases as mass increases. This is true even if the energy input of the throw remains the same, just as it does for the double pendulum experiment here. If that is so, we should see an increase in the force exerted to accelerate the racquet's center of mass as more mass is added to the racquet. This is indeed what we see (Figure 20):
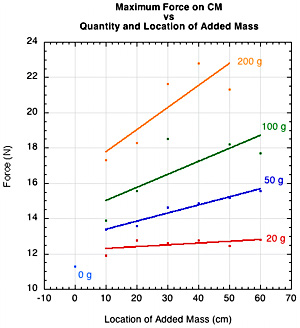
Figure 20 — Force vs Added Mass As mass and/or location distance from the axis is increased, so to does the force exerted on the CM of the racquet.
This is significant if we consider that for a constant energy swing, the racquet speed decreases whenever mass is added anywhere to the racquet, even though the force on the racquet is increased.
11. Swingweight, Center of Curvature, and "True" Axis of Rotation
The concept of swingweight (moment of inertia) is essential to understanding rotational motion. Swingweigt is the resistance to rotation about a particular axis. A force applied a distance from the axis is necessary to initiate rotation. The magnitude of the force times the perpendicular distance from the line of force to the axis is the torque. Higher swingweight requires a greater torque to initiate motion. That can be achieved by increasing the force or the distance from the axis or both.
In tennis, swingweight is usually measured with a Babolat RDC machine that measures about an axis 10 cm from the butt end of the racquet (or the "Do-It-Yourself Pendulum Method"). A tennis swing does not rotate about this axis, nevertheless, it is the relative comparisons between racquets that is important in most circumstances. However, the 10 cm-swingweight can be used to calculate swingweight about any other axis. This is accomplished using the parallel axis theorem:
Ip = Icm + Md2 (Equation 6)
where Ip is the moment of inertia about the parallel axis, Icm is the swingweight about the center of mass, M is the mass of the racquet in kilograms, and d is the distance of the axis from the center of mass in centimeters.
In this case the RDC swingweigt is the parallel axis swingweight so,
Icm = Irdc - Md2 (Equation 7)
Then, to determine the swingweight of the racquet about an axis, say 20 cm from the end of the racquet, the formula would be,
Ip20 = Icm + M(b + 20)2
where b ("b" for balance point) is the distance of the center of mass from the butt end of the racquet.
If you add mass anywhere to the existing racquet, it changes the mass, balance point, and swingweight. However, if you already know the swingweight about your axis of interest, then the new swingweight will be,
I2 = I1 + md2 (Equation 8)
where I2 is the new swingweight, I1 is the old swingweight, m is the mass to add, and d is the distance of the additional mass from the axis.
Figure 21 shows how swingweight changes depending on the axis of rotation chosen. A mass of 10 grams is added at 2 cm from the end of the racquet (shown as black square) or at 60 cm from the end (not shown). That mass is 8 cm from the RDC-axis (10 cm from end), 28 cm from the axis at the center of mass axis, 2 cm from the axis and the end of the racquet, and 17 cm from an axis 15 cm off the end of the racquet. The resulting change in swingweight is displayed in the color-coded boxes for both the 2 cm and 60 cm locations of the added mass.
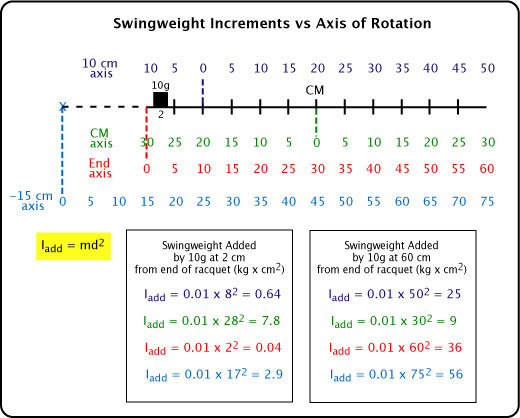
Figure 21 — Change in swingweight around designated axes of rotation.
Obviously, the extra effort to swing the heavier racquet will depend on which axis you are swinging about. No matter which axis that is, if you add mass to the axis itself, it will take no extra torque to rotate the racquet around that axis. However, it will take extra torque to rotate it about any of the others. And extra mass, no matter where you add it, will take extra force to lift and to move in a straight line (no rotation).
If the effect of added mass on swingweight depends on its distance from the axis of rotation, what happens if that distance changes during a swing? For example, the distance of the center of mass of the racquet changes relative to the elbow axis as it swings. It is cocked at 90 degrees to the forearm on the backswing, is near straight to the forearm at impact, and is again rotated toward the axis on the follow-through. If we consider the racquet as a point mass rotating around the elbow then its swingweight is Icm + Md2, where Icm is the swingweight about the CM, M is the mass of the racquet and d the distance of the CM to the axis. The distance, d is continuously changing, so swingweight about that axis is changing also, as displayed in Figures 22 and 23. The torque required to rotate that racquet around the elbow axis will vary throughout the swing (this is also true about the shoulder). However, the swingweight around the wrist axis will not change nor will the force required to swing around that axis, because the CM does not change its distance from the wrist during the swing (the same is true for RDC swingweight [10 cm axis] and swingweight about the CM).
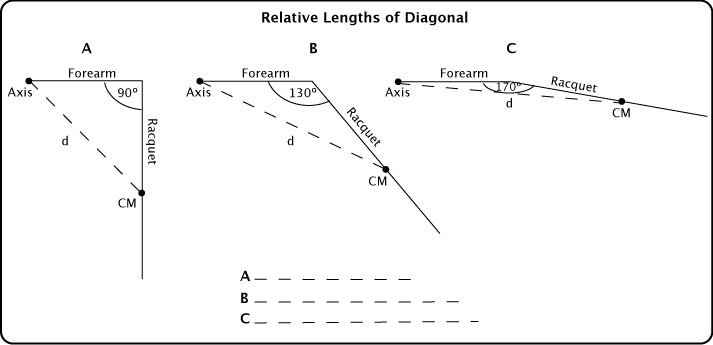
Figure 22 — Swingweight of racquet rotating around the forearm axis varies as the distance between the forearm axis and racquet CM varies.
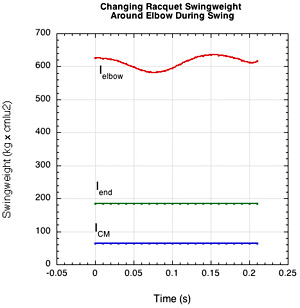
Figure 23 — Changing Swingweight About Elbow Axis. As the racquet starts forward, the head lags behind, moving the racquet CM closer to the elbow and the swingweight decreases as the distance decreases. As the swing progresses, the CM rotates forward increasing its distance from the elbow and increasing the swingweight. The swingweight about the CM and the end remain constant.
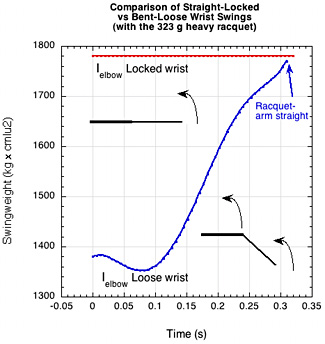
It follows that since part of the racquet rotation occurs about the elbow, swing techniques that have different racquet CM paths of travel will have different swingweights about the elbow and this should show up in racquet tip speed. A straight-armed, locked wrist that keeps the CM a constant and maximum distance from the elbow axis will have a greater swingweight about the elbow and result in slower racquet speed (Figure 24).
 (b)
(b) 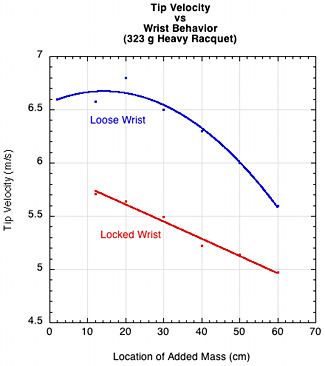
Figure 24 — Comparative Wrist Behaviors (a) Swingweights at elbow for loose and locked wrist. (b) Racquet tip speeds for loose vs locked wrist.
The question, then, is what axis does a tennis stroke rotate around? Obvious candidates are the wrist, the elbow, the shoulder, or the center of the body. In reality, different parts of the swing are dominated by different axes, and the net result is an axis that lies somewhere in-between them all. Furthermore, it depends on what kind of swing a player has. If we knew the true center of rotation, couldn't we take the swingweight around that as the best predictor of racquet behavior?
Center of Curvature. Often cited as a candidate for this "true" axis of rotation is the center of curvature. This is the projected center of the circle that is delineated by the arc drawn by 3 successive points along the path of a selected point on the racquet. We will use the CM as our point. The radius of this circle is known as the radius of curvature. The longer the radius the less the curvature and vice versa.
The equations for curvature are as follows:
Curvature = K = |(d2y) /dx2 / (1 + (dy/dx)2)1.5| (Equation 9)
Where x and y are the coordinates of each successive point along the path of the CM.
The radius of curvature is:
Radius = R = 1 / K (Equation 10)
The center of curvature coordinates are:
X center = x - ((dy/dx)(1 + (dy/dx)2) / d2y/dx2) (Equation 11)
Y center = y + (1 + (dy/dx)2) / d2y/dx2) (Equation 12)
The center of curvature constantly changes throughout the swing — often radically — as the path swept by the CM varies between more cicular and linear sections of the swing. The most curvature is created by rotation about the CM, next the wrist, and then the elbow and shoulder. Rotation about axes further from the CM straighten the arc compared to those closer. The amount of curving-straightening will then depend on the angular speed about any one axis. Movie Screen 2 shows the many centers of rotation as the double pendulum swing progresses. The setup shown is with the 323 gram heavy racquet with no spring simulating the wrist force. Because there is no additional wrist torque, the CM path will be more linear than it would otherwise be and the center of rotation a bit further from the CM. The green dots trace the path of the CM. (Note: Advance the movie one frame at a time to see the center location highlighted with a circle around the triangle.)
Video 2
Center of Curvature
Movie Screen 2 — Center of Curvature. The center of rotation of the CM varies as the racquet rotation speed varies about the CM (at very beginning), wrist, and elbow. The center of curvature is concentrated at points between the wrist and the elbow for most of the swing.
Note on movies: It is sometimes easier to see high speed movies by advancing one frame at a time using the right or left arrows on the keyboard or by scrolling the movie progress bar.
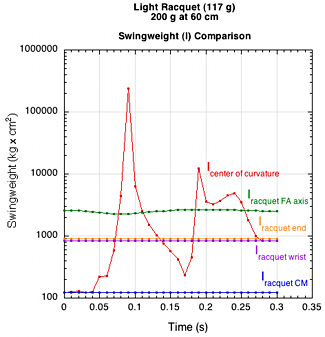
The swingweight can be calculated about the instantaneous center of curvature. Figure 25 shows the graph of one such calculation for the swing of the light racquet with 200 g added at 60 cm and the digitized image of the swing.
 (b)
(b) 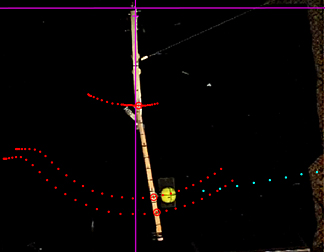
Figure 25 — (a) Five swingweights throughout the swing of 117g racquet with 200 g added at 60 cm; (b) the digitized image of the swing for the graphs in (a).
The spikes on the center of curvature swingweight are portions of the swing path that are essentially straight. That means there is almost no curvature so the center of the "curve" goes out toward infinity (6 meters beyond the end of the racquet in this case). During those portions, the CM is travelling a straight line and mass, not swingweight, is the primary resistance to motion. When the curvature swingweight drops between the wrist and CM swingweights, the pulling force of the string has stopped, the forearm is slowing and most of the rotation of the racquet is around the CM. The ball is hit at about 0.21 s which decreases racquet rotation and straightens out the path. For a swing path such as this, it is tempting to say that all curvature swingweight points above the forearm-axis-swingweight are essentially for straight line travel and not relevant swingweights, and as such, acceleration of the CM depends on the mass of the racquet during that phase. That leaves primarily the time before impact that is between the forearm and wrist swingweights as, perhaps, the truest, most relevant swingweights for determining the final velocity of the impact location.
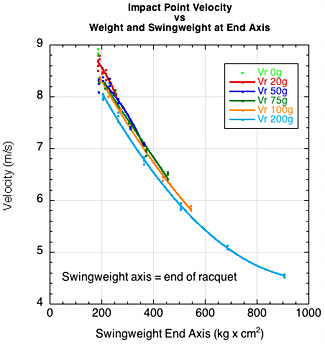
We saw in Figures 4 and 5 that swingweight is the best parameter we have for predicting the speed of a tennis racquet at impact. We chose the end of the racquet as the relevant axis in those graphs. The results were very good, but can they be made even better by choosing another axis — perhaps one lying somewhere between the forearm and the racquet, as indicated by the center of curvature results? Several trial and error choices were made with the best result being for an axis 9.5 cm beyond the end of the handle (Figure 26).
 (b)
(b) 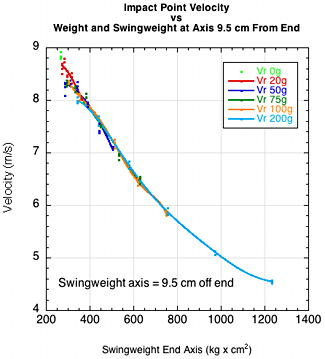
Figure 26 — Comparative swingweight axes. (a) Racquet impact location speed vs swingweight about end of racquet and mass added to racquet. (b) Racquet impact location speed vs swingweight about axis 9.5 cm from end of racquet and mass added to racquet.
The end of the racquet is obviously an adequate axis upon which to base our predictions of racquet speed changes due to changing mass distribution. It is a fixed location and easy to measure or calculate. A player is not interested in the actual increase in force will be necessary to swing a racquet, but only in which racquet will be easier to swing. Measuring swingweight at the end is convenient because if a racquet's swingweight is greater around that axis, then it is greater around all other primary axes (elbow, shoulder, body, center of curvature). More research must be done to confirm that there is always a "true" axis of rotation where all the curve fits for all customizations will converge and not just an artifact of, say, the geometry and constraints of the experiment.
IV. CONCLUSION
The relationship of mass distribution and various performance variables has been explored. The main conclusions are these:
- Any mass, anywhere decreases racquet speed.
- Added mass increases ball speed up to a point, then decreases it.
- Added mass increases power potential, plow-through, hittingweight, whip-through up to a maximum and then decrease.
- Added mass causes the racquet to swing faster relative to the forearm.
- Swingweight is the best predictor of racquet performance.
- Added mass can make the racquet seem to swing faster.
- A "true" center of rotation for calculating swingweight might exist.
- Swingweight about certain axes is variable during the swing.
- Axes change in contribution to rotation throughout the swing.
- Swings are a combination of linear and rotational motion. Added mass affects both.
- A loose wrist swing had greater racquet and ball speed than locked wrist swing.
- When mass increases, more force is automatically created to swing the racquet, but not enough to increase racquet speed above the no added mass condition.
- If you want more racquet head speed and more mass, you have to put more energy into the swing and swing faster.
Three graphs sum up the big picture as to the influence of adding mass by location to a racquet. Figure 27 shows the change in racquet speed (27a), ACOR (27b), and ball speed (27c), which is the result of the first two. Racquet speed decreases with both mass and greater distance, ACOR increases and flattens out, and ball speed first increases as added power makes up for decreased head speed, and then declines as both head speed and power decline.
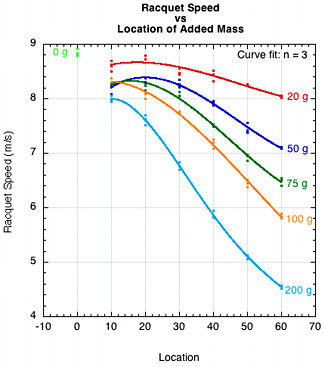 (b)
(b)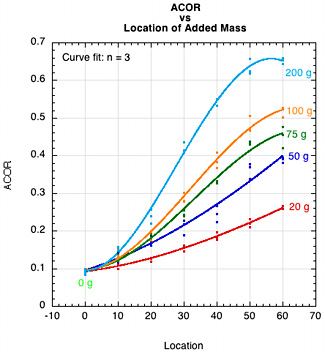
(c)
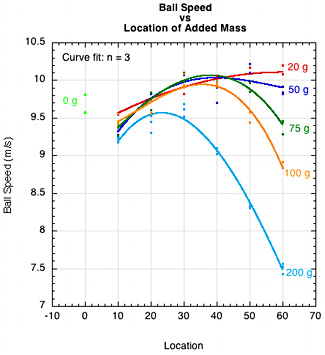
Figure 27 — Summary. (a) Racquet speed vs location of added mass, (b) ACOR vs location of added mass, (c) Ball speed vs location of added mass.
These results are all for a constant energy input. Everything changes if you can swing faster. If you add mass and you increase your energy, you can increase swing speed, ACOR and ball speed. Moral to the story: At very low swingweights (less than 200-250 kg x cm2 RDC swingweight) there is a free lunch and you can get more ball speed for the same effort, but at swingweights typical of play, you get out what you put in.
V. APPENDIX
A1. THE GEOMETRY
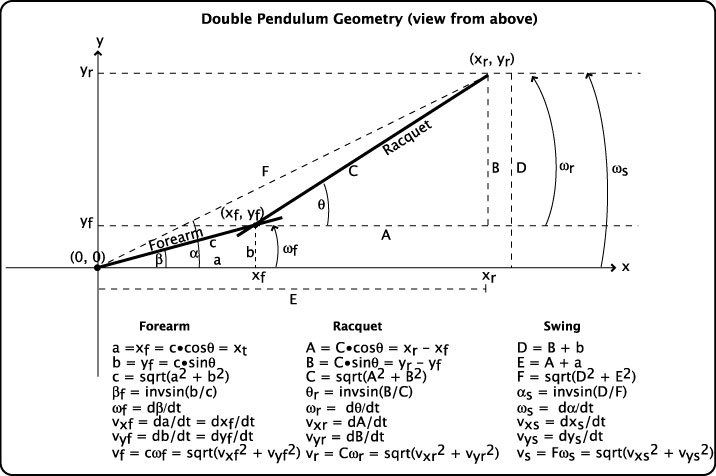
Figure 28 — Double Pendulum Geometry.
References
1. Jorgensen, T. (1994), The Physics of Golf 2nd Ed., Springer-Verlag New York.
2. Cross, R. (2011), "A double pendulum model of tennis strokes," Am. J. Phys. 79(5) 470-476.
3. Cross, R. (2011), "The Double Pendulum in Tennis," https://twu.tennis-warehouse.com/learning_center/doublependulum.php.
4. Cross, R. (2005), "A double pendulum swing experiment: In search of a better bat," Am. J. Phys. 73, 330-339.
5. Cross, R. (2004), "Physics of Overarm Throwing," Am. J. Phys. 72, 305-312.
6. Brody H, Cross R, Lindsey C (2002) The Physics and Technology of Tennis. Racquet Tech Publishing, Solana Beach CA, 124-126.
6. Brody H, Cross R, Lindsey C (2002) The Physics and Technology of Tennis. Racquet Tech Publishing, Solana Beach CA, 145-146.

