INTRODUCTION
We normally expect topspin from a racquet that is swinging upward, tilted forward or both. And we expect backspin if the racquet is swinging downward and tilted backward. We also expect more topspin when hitting balls descending to our racquets and less when ascending. And we expect that we will get less spin if we have to reverse the incoming spin and more if we are hitting with it. But we are often surprised by our actual results.
Spin generation is all about the relative motion between the contact surfaces of the ball and strings. The relative motion is determined by the ball's incident spin, speed and angle and the swing speed, angle, and tilt of the racquet. The net effect of all these variables can lead to results that are counter-intuitive or contrary to conventional wisdom or rules of thumb. This is especially true when it comes to bounce spin and angle.
In order to see and analyze some of these results we created some off-court demonstrations that attempt to isolate various variables involved in spin generation. In order to dissect the anatomy of spin, we have used various bounce surfaces — court sections glued to wood planks, sandpaper taped to planks, and racquets performing simplified impacts. All videos are filmed at 300 fps. Some videos have moving bounce surfaces and others are stationary, and some surfaces are moving vertically as in a tennis stroke and others are horizontal as in a bounce off a court.
The demos show that just because you swing upward does not mean you will get topspin, swinging down does not mean you will get backspin, and swinging flat does not mean no spin. You can get top, back, and no spin from all swing trajectories. The result depends on the net sum of all incident ball speed, angle, and spin and racquet speed, angle, and tilt. The result of this sum is known as the relative path — the path of the ball relative to the racquet. Relative path diagrams accompany most of the demos below. These are essential in understanding the direction and spin of the bounce.
As a matter of convention, a ball has topspin if the rotational motion at the top of the ball is in the same direction as the linear direction of the center of the ball. It is backspin if it is in the opposite direction. If there is no horizontal motion of the ball, then spin will be referred to as clockwise or counter-clockwise. We will also refer to the spin speed and direction at the contact point between the ball and racquet. Here we will often refer to the spin direction as upward or downward on the strings. The direction is important to the resulting spin of the shot.
BASIC BOUNCES
The first five videos are simply examples of basic bounces off a secured, stationary segment of court surface. These will give us a contextual baseline for when we graduate to more complicated bounces off moving surfaces and swinging racquets.
Video 1
Incident at 90 degrees, no spin
Movie Screen 1 — A ball incident at 90 degrees with no spin. There is no relative horizontal motion between the ball and surface so there is no horizontal friction force. The bounce is therefore perpendicular with no spin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 2
Incident at 90 degrees, clockwise spin
Movie Screen 2 — A clockwise spinning ball incident at 90 degrees will bounce to the right (in the direction of spin) with less spin. The relative motion of the bottom of the ball is to the left and creates a friction force to the right, pushing the ball in that direction and creating a counter-clockwise torque, lessening the clockwise spin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 3
Incident at 90 degrees, counter-clockwise spin
Movie Screen 3 — A counter-clockwise spinning ball incident at 90 degrees will bounce to the left (in the direction of spin) with less spin. The relative motion of the bottom of the ball to the right creates a friction force to the left, pushing the ball in that direction and creating a clockwise torque to lessen the counter-clockwise spin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 4
Incident at oblique angle, no spin
Movie Screen 4 — A ball incident at an oblique angle with no spin will bounce in the same direction with topspin. The motion of the incident ball's contact surface is to the right so a friction force (and resulting torque) acts to the left, slowing the ball, increasing the bounce angle, and generating topspin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 5
Incident at oblique angle, topspin
Movie Screen 5 — A ball incident at an oblique angle with topspin will bounce in the same direction with increased topspin. The incident contact speed at the bottom of the ball due to spin is to the left, while the contact speed due to the trajectory is to the right. The net speed, in this bounce, is to the right, so friction slows the ball, increases the bounce angle, and increases the topspin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
BOUNCES WITH VERTICALLY MOVING SURFACE
Relative Motion — The bounce of a ball off the court surface is easily explained since the court remains at rest. The bounce off the strings of a racquet is more difficult to explain since the racquet is moving when it strikes the ball. However, the bounce result can be predicted in terms of the relative speed of the ball and the racquet. This allows us to pretend that the racquet is at rest, in which case the bounce is essentially the same as the bounce off the court. Not exactly the same, since the racquet is much lighter than the court so the bounce speed off a stationary racquet will be smaller.
A simple example is demonstrated in Videos 6 and 7. Video 6 shows an a ball incident from left to right without spin onto a stationary surface and then bouncing to the right with spin. Video 7 shows the surface moving left to right while the ball is incident left to right at the same horizontal speed. That is, the ball moves the same horizontal distance as the surface during any given time. The relative speed of the ball and the surface, in the horizontal direction, is zero. As a result, there is no relative horizontal motion of the ball and the surface when the ball strikes the surface, which means that the ball does not slide across the surface during the bounce. Since there is no sliding friction force on the ball in this case, there is no rotation of the ball during the bounce. The ball therefore bounces without spin.
Video 6
Relative Motion 1: Bounce off stationary surface
Movie Screen 6 — A ball incident left to right without spin onto stationary surface bounces left to right with spin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 7
Relative Motion 2: Bounce off moving surface
Movie Screen 7 — A ball incident left to right without spin onto suface moving in same direction at same speed bounces left to right with no spin.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
In order to see what is happening in Video 7, we use some simple geometry to redefine the speed and angle of the ball in relation to the surface, thus pretending the surface is at rest. The technique is explained below, and each of the videos 8-18 is accompanied by a shot analysis diagram showing the result. The technique is known as changing the frame of reference.
The Technique (Figure 1 shows the technique as applied to Video 7 above) — Step 1 in the figure shows the speed and directions of the incident and outgoing ball, and the moving surface. These paths were measured 0.05 seconds before and after impact. Next (step 2), take the surface path line and place it with its end point at the beginning point of the ball path. Connect the two paths by drawing a line from the start point of the surface path to the end point of the ball path. This maneuver represents subtracting the surface path from itself, leaving no path, and adding it to the ball path. This combined path is the path of the ball relative to the surface. This path represents the relative speed and angle of impact of the ball to a stationary surface. Now it is easier visualize what the bounce will look like and why.
Determining Relative Motion
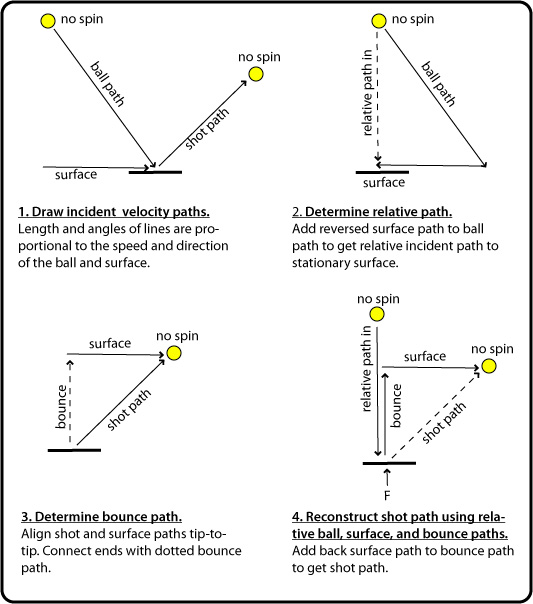
Figure 1 — Technique for drawing relative path diagrams.
To get the actual bounce path (step 3), take the impact point of the surface arrow and place it to the end point of the shot path. Connect the two open ends. This connecting path is the bounce path. And last (step 4), connect the surface path and bounce path and we are back to the shot path.
This relative path diagram in Figure 1 shows the non-spinning ball falling and bouncing along the same path with no horizontal motion to the surface. This is what you would see if you dropped a ball on the floor of a speeding train. An observer on the side of the tracks would see the ball bounce along the trajectory of the shot path.
Usually the incident ball will be spinning, however. The rebound spin will be determined by the combined contact velocity (vc) of the ball's linear speed parallel to the surface plus the rotational velocity of the incident spin. The spin at the contact point may be in the same or opposite direction of the linear motion. A friction force will act in the direction opposite the net contact velocity. From the videos below it is easy to see the direction of vc due to the rebound angle and resulting spin. The shot analysis diagrams show the direction of the friction force in step 4 of each diagram.
Video 8
Incident falling topspin, rising surface
Movie Screen 8 — A ball incident to the surface at a descending angle with topspin will bounce in the same direction with topspin. That means that the spin reversed direction during contact. The surface is moving vertically upward as in a topspin stroke with a racquet. Notice that the ball still bounces downward even though the surface is moving upward and the spin has reversed direction. The angle has been partially "turned around" in that the angle to the surface is greater for the bounce than for the incident ball.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 8 Shot Analysis
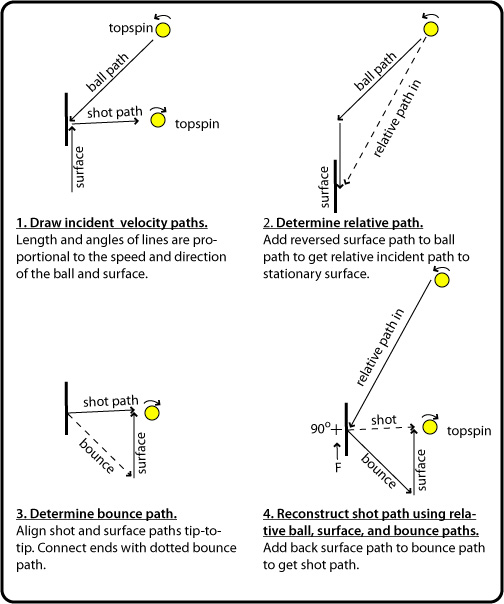
Figure 2 — Relative path diagram for incident falling topspin, rising surface.
Video 9
Incident 90 degrees topspin, falling surface
Movie Screen 9 — A horizontally travelling topspin ball incident with a surface moving vertically downward will bounce downward with backspin. Out-going spin is in the same counter-clockwise direction as the incident spin and has increased. Spin has not been reversed even though by convention we say that the incident ball has topspin and the rebound spin has backspin. The incident ball is effectively rising to the racquet as can be seen by watching it "ascend" past the white lines on the board. Thus, friction will push the bottom of the ball downward and rotate it counter-clockwise (backspin).
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 9 Shot Analysis
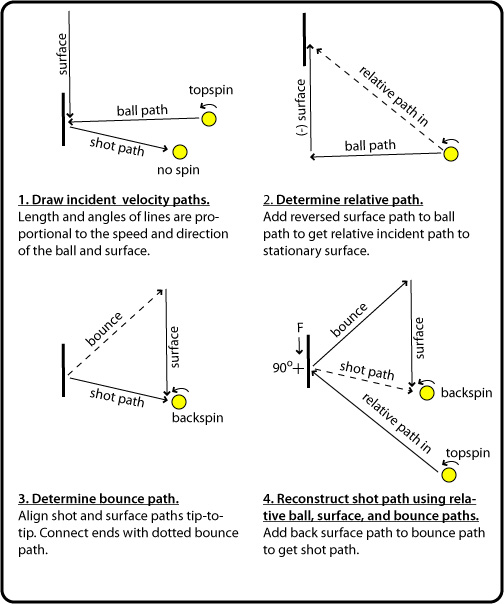
Figure 3 — Relative path diagram for incident 90 degrees topspin, falling surface.
Video 10
Incident falling topspin, falling surface
Movie Screen 10 — It is somewhat shocking to see a rebound with no spin. But because the ball is falling much faster than the surface and the spin is in the same direction, the vc is downward and the friction upward. Therefore the ball is pushed backward and the spin is decreased (though not reversed) to zero.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 10 Shot Analysis
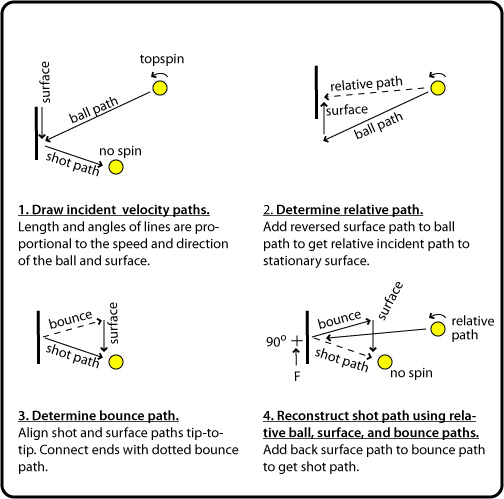
Figure 4 — Relative path diagram for incident falling topspin, falling surface.
Video 11
Incident rising backspin, falling surface
Movie Screen 11 — The only circumstance where you would see a rising ball with backspin is if your opponent slices the ball and you hit a volley. The ball will always bounce off the court with topspin. This rebound is as you might expect. The incident ball is rising, vc is upward, and the surface downward, all of which increase the upward relative speed of the ball to the surface. Friction therefore is acting downward, increasing backspin and the rebound angle from the strings (i.e., closer to the perpendicular).
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 11 Shot Analysis
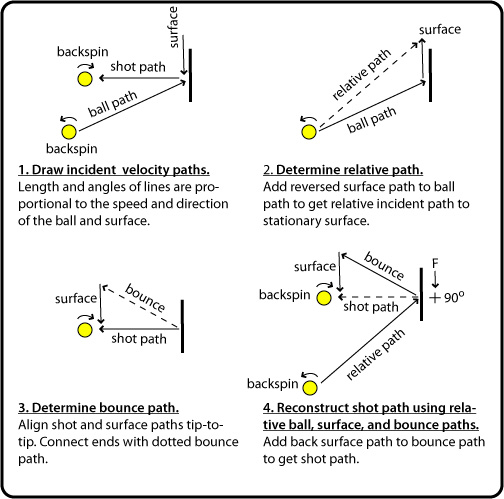
Figure 5 — Relative path diagram for incident rising backspin, falling surface.
BOUNCES WITH HORIZONTALLY AND VERTICALLY MOVING RACQUET
Video 12
Incident rising topspin, flat swing
Movie Screen 12 — Because the swing is flat, the bounce is almost the same as Video 5. Because the ball is hit almost at the top of the bounce and the racquet is tilted slightly forward, the incident angle is upward but very close to perpendicular. Therefore, at the contact point, the spin speed downward is greater than the ball speed upward, so friction is acting upward, reducing but not reversing the incident spin direction.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 12 Shot Analysis
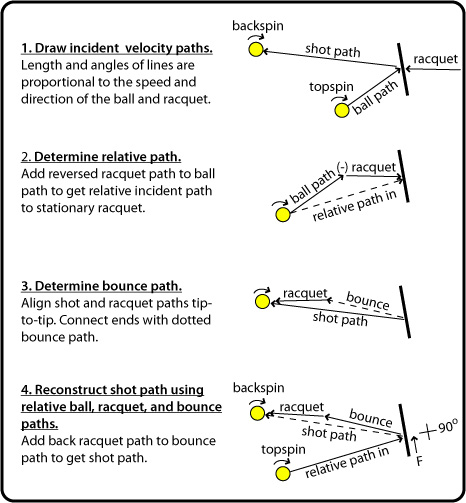
Figure 6 — Relative path diagram for incident rising topspin, flat swing.
Video 13
Incident rising topspin, rising swing
Movie Screen 13 — The ball is hit at the top of the bounce so the incident ball path is almost horizontal. The high racquet speed upward translates to high ball speed downward when we change our view to be relative to the racquet. At the contact point, the spin speed is also downward, so friction acts upward, reversing the spin direction.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 13 Shot Analysis
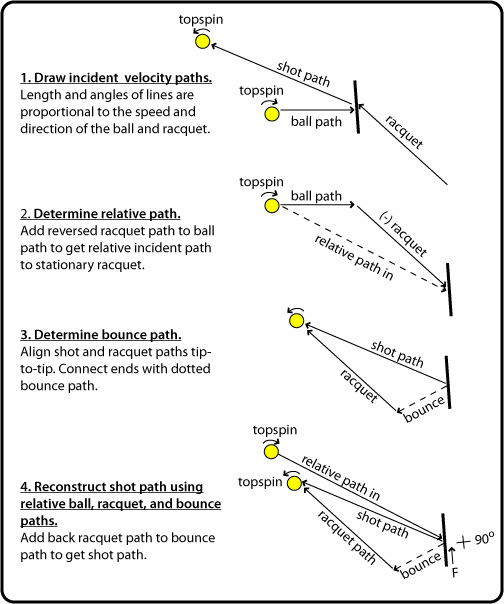
Figure 7 — Relative path diagram for Incident rising topspin, rising swing.
Video 14
Incident rising topspin, falling swing
Movie Screen 14 — Adding the paths of the racquet and ball together to get the relative ball path to the racquet, we see that the incident upward speed is quite high and at a substantial angle to the racquet face (which increases that angle by tilting slightly backward). Although the spin direction at the contact point is downward, the net speed and direction of that point is still upward. Friction therefore acts downward, bringing the rebound angle closer to horizontal and increasing the speed of the existing clockwise spin. Thus, spin direction is not reversed even though terminology is — incident topspin becomes rebound backspin from the observer's point of view.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 14 Shot Analysis
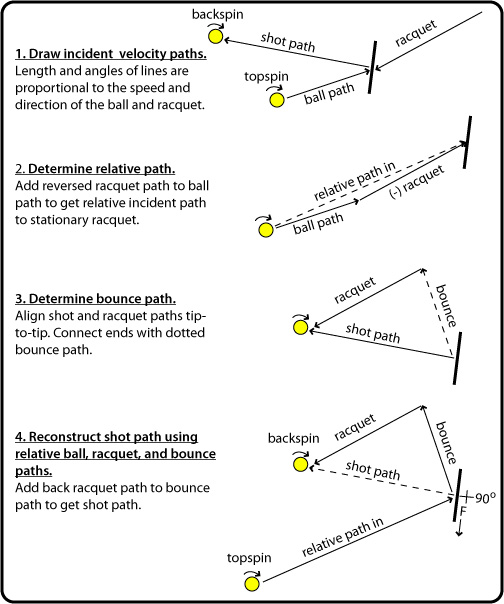
Figure 8 — Relative path diagram for Incident rising topspin, falling swing.
Video 15
Incident rising topspin, forward-tilted flat swing
Movie Screen 15 — This shot is very similar to Video 10 except that the racquet is tilted much further forward. The effect of the tilt depends on the direction of the incoming ball. In this case, the tilt was enough to make the relative incident path downward across the racquet face, in spite of the incident ball's ascending trajectory. The resultant upward friction was enough to just barely reverse the spin direction. The shot path was downward to the observer's point of view, but still greater than the perpendicular to the racquet face.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 15 Shot Analysis
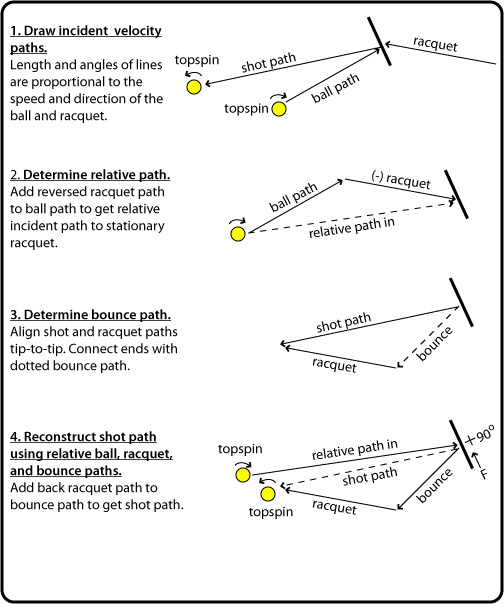
Figure 9 — Relative path diagram for incident rising topspin, forward-tilted flat swing.
Video 16
Incident rising topspin, forward-tilted rising swing
Movie Screen 16 — This is a classic example of a topspin shot — a fast, upward swing with forward tilted racquet. The relative incident path is descending at a steep angle with spin at the contact point also directed downward. The friction force acts upward, resulting in spin reversal and a substantial topspin exit. It is interesting to note how the bounce path is actually backwards to the observer but the racquet path redirects the ball into a normal trajectory.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 16 Shot Analysis
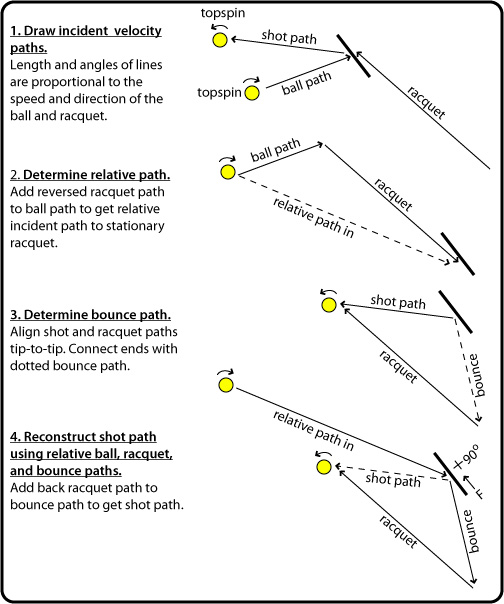
Figure 10 — Relative path diagram for incident rising topspin, forward-tilted rising swing.
Video 17
Incident rising topspin, backward-tilted flat swing
Movie Screen 17 — Particularly due to the tilt, the relative incident path is at a large angle from the perpendicular to the racquet face. The ball is therefore moving faster upward across the strings than the spin is moving down. As a result, friction acts downward, increasing the existing clockwise spin and pushing the shot path down compared to the bounce path.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 17 Shot Analysis
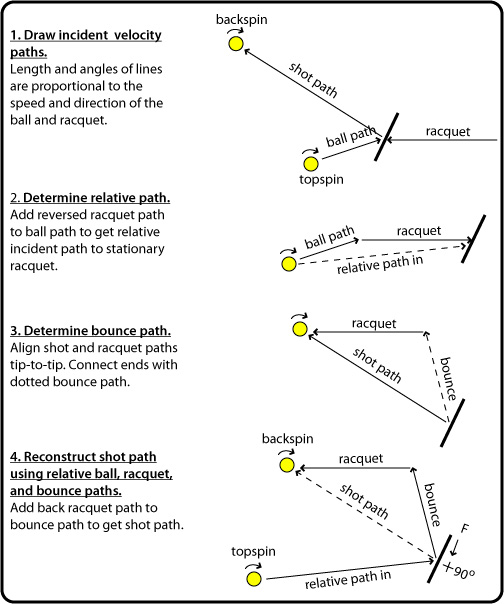
Figure 11 — Relative path diagram for incident rising topspin, backward-tilted flat swing.
Video 18
Incident rising topspin, backward-tilted falling swing
Movie Screen 18 — This is the classic slice shot — rising ball to the backward-tilted, descending racquet. The incident relative angle is far from the perpendicular, so the upward ball speed parallel to the strings is greater than the downward spin speed at the contact point. Friction acts downward, increasing the existing clockwise spin and lowering the outgoing trajectory compared to the relative bounce path.
(Note: Use "double-arrow" movie controls for frame-by-frame play.)
Video 18 Shot Analysis
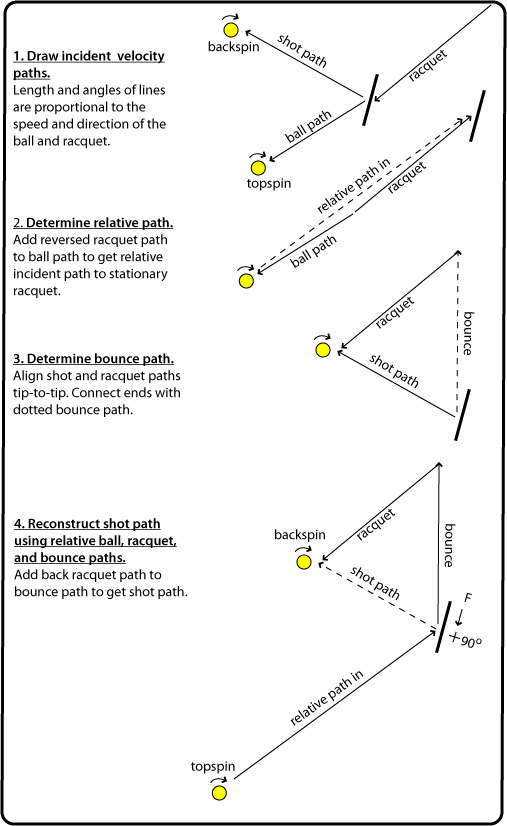
Figure 12 — Relative path diagram for Incident rising topspin, backward-tilted falling swing.
V. CONCLUSION
You don't have any control over the incident ball parameters, except maybe choosing whether to hit the ball on the rise, top of the bounce, or on the descent. What you do have control over is the speed, angle and tilt of the racquet. Altering these will change the contact velocity of the ball relative to the strings. For topspin, the secret is to have maximum vc. The reason is this: Even if the ball path is upward, if the racquet path is also upward but at a much greater speed or angle, then the relative path will be downward. Now spin speed and linear speed across the strings will be downward. Friction will then act upward, slowing the downward ball speed and reversing and increasing the upward spin speed. When the sum of the downward ball speed and the upward spin speed are equal but opposite directions, vc will be zero. Now there is no relative motion between the surfaces and friction will decrease to near zero. The greater incident vc, the greater the amount of linear speed that must be turned into spin speed in order to reach the equal but opposite condition. The result will be more topspin. If the scenario is the same but the incident ball is descending, then it will take even more linear spin turned into topspin before vc becomes zero.
The same reasoning applies to a slice except that maximum backspin spin occurs if you hit the ball on the rise and less backspin if you slice a descending ball.
Most players know that you get more spin if you swing faster and steeper. But not everyone knows why the results can be so different from situation to situation, from opponent to opponent, and from court to court. The above exposition has tried to explain how, when, why and how much spin changes during impact scenerio. It is possible that diagraming your opponents' shots could give you clues as to what shots to best use against them.

