I. Friction and Spin
Friction is important to spin, but not in the sense that most people think it is. In the past, two assumptions were the foundation for the conventional wisdom that (1) a rough string surface creates more spin by increasing the string's bite, grab and push on the ball, and (2) that inter-string motion would lessen that grabbing and thus should be minimized. So, to gain maximum spin, the goal was to use a string with both a high ball-string friction and a high string-string friction to create a rigid surface parallel to the stringbed.
As so formulated, both of these assumptions have proven incorrect. First, experiments show that for a tangentially noncompliant surface, the spin will be nearly the same for all magnitudes of string-ball friction for impact angles typical for tennis shots. For reasons explained below, both rough and smooth strings will produce the same spin on a laterally rigid surface.
Second, recent experiments (Spin and Material, Spin and String Movement, Spin and String Pattern and String Snap-Back and Spin) have also demonstrated that sideways motion of the main strings during contact with the ball actually contributes to increasing spin. This sideways movement exerts a torque on the ball when it snaps back into position, thus causing topspin. Polyesters have been shown to add about 20% more spin than nylons. Polyesters can differ up to about 15% from each other in spin production while nylons might vary by 20% from each other. And the difference between the spiniest polyester and stickiest nylon is almost 50%. Virtually all this difference is attributable to the amount of torque supplied by the sideways movement and snap back of the main strings.
The role of ball-string friction in this process is that it influences both the amount of lateral string movement and the torque the snap-back exerts on the ball (though the magnitude of its contribution is yet to be ascertained by experiment). It is here that ball-string friction contributes to the difference in spin performance between string models, but only if the strings move. Otherwise, ball-string friction produces about the same spin for every string. And whether the strings move or not depends on the static and sliding friction between strings.
First we will explore why the spin contribution of ball-to-string friction depends on whether the strings move or not and then we will examine the role of static friction between strings in string movement. Sliding friction is discussed on another page: Spin and Sliding Friction.
II. Ball-To-String Friction
1. On a rigid surface.
For a typical topspin shot, almost all of the work done to change the spin of the incoming ball is achieved by the sliding friction between the strings and the ball. One might think, therefore, that strings with a rougher surface might grab the ball better and produce more spin. However, when all is said and done, ball-string friction, whether it is great or small, changes the spin by the same amount on a rigid surface. The grabbier string will do it more quickly (say, in 3 ms) than the less grabby one (say, 4.5 ms), but they both change the spin the same amount and they both accomplish this during the approximately 5 ms impact duration. The first does it with a larger force in a shorter time, and the second does so with a smaller force for a longer time. In both instances the ball ends up with the same amount of spin that can be attributable to ball-string friction.
This 'same spin' result is true whether the string is a rough or smooth, thin or thick, or round or square. The reason is that both high- and low-friction string surfaces change the ball's forward motion and spin in ways as to cancel each other and make friction ('sliding friction') disappear. This occurs when the ball transitions from sliding mode to biting mode (where static friction takes over). This happens at the contact area when sliding friction has changed the ball's spin speed and direction and slowed its progress across the strings to the extent that the ball's periphery comes to spin at the same speed backwards as the entire ball is moving forward. In other words, the forward and backward speeds cancel, there is no relative motion of the strings and ball, the contact point is thus at rest, and there is thus no sliding friction, which is a reaction force to such motion. No motion means no sliding friction, which, also, means no significant additional spin due to friction (actually, there are some complicated friction related events that occur after biting, but they tend to cancel and are not necessary for the present discussion). It is true that most cases the rough string will create a greater sliding friction force on the ball, just as you would expect, but as far as spin is concerned, that just gets you to the same spin a millisecond or so sooner than with a smooth string.
Biting occurs for all topspin shots except those at very oblique angles of impact with the ball. Most topspin shots are hit from 0-50 degrees away from head-on impact. At greater angles than this, the ball may not bite and will slide across the strings. In these cases, a greater friction surface will increase spin. But such a situation rarely occurs except in extreme topspin lobs.
2. On a tangentially deformable surface.
All the above holds for impact on a laterally elastic surface as well. The bottom of the ball will bite and achieve a relative velocity of zero to the strings, sliding friction will cease, and spin generation will, for an instant, come to a stop. Up to the biting stage, all strings produce the same spin. That used to be considered the end of the story. But more happens. During the sliding stage, the ball-string friction will help determine how far and fast the main string(s) will move. Further, it will influence the magnitude of the torque on the ball upon snap-back. Without the string moving, energy that doesn't spin the ball remains unavailable or is "burned up." If that friction is also used to store energy in laterally stretched string, then saved energy is available for ball spinning. The role that ball-string friction plays in spin is quite ironic: the reason it contributes to spin is that it is effective in doing that which we were formerly trying to prevent it from doing — moving the string.
Evidence for the snap-back theory is presented more fully in another article: String Snap-Back and Spin. For the rest of this article, we will explore the static string-to-string friction that influences the initiation of string movement and is thus an important property when comparing strings for spin potential.
III. String-To-String Friction (Static)
If the strings don't move sideways, all strings produce about the same spin. If they do move, it is the movement and stretching of the mains that determines the different spin outcomes between string types. And whether or not the strings move is in part determined by the magnitude of the friction between strings — the lower the static friction, the easier it is to initiate string movement, and the lower the sliding friction, the easier it is to maintain the string's movement. The result is greater spin (assuming the strings snap back while the ball is still on them).
The figure below shows the coefficient of static friction (COF) vs the force pressing the strings together for several popular "spin friendly" polyesters. The COF is the ratio of proportionality of the friction force between strings to the force pushing them perpendicularly together (the "normal" force). The normal force arises primarily from the force of impact and secondarily from the string tension. The COF indicates how much the friction force increases as the normal force increases. This depends ultimately on the atomic attraction between the two contacting surfaces which in turn depends on the atomic level topography of those surfaces.

Figure 1 — COF vs Normal Force.
Static friction between strings is determined by the surface characteristics of the main and cross that are moving against each other as well as the force pushing them together. Strings are pushed together by weaving and then pulling to tension. But the main compressive force is created by impact with the ball. The harder you hit the ball, the greater the normal force pushing the strings together and the more friction that will exist between strings. An oblique impact also causes a tangential force component parallel to the strings. To move the strings sideways, this has to be great enough to overcome the friction between the strings. And then, the string must retain enough elastic energy stored in its sideways stretch to overcome that same friction in returning to its starting position.
So, changing materials or tensions will change the friction between strings, but will different materials or combinations of materials react differently at different forces? To find out, we have tested several strings and combinations of strings to measure the friction over a range of forces pressing the strings together (defined as the force perpendicular, or normal, to the string surface).
At any given normal force, friction is determined by the coefficient of friction, μ.
F = μN
Where F is friction, μ is the coefficient of friction and N is the normal force. The string with the lowest coefficient of static friction will have the least static friction, will be easier to set into motion, and will tend to increase spin the most. Below are two graphs illustrating the coefficient of static friction at different normal forces for different materials.
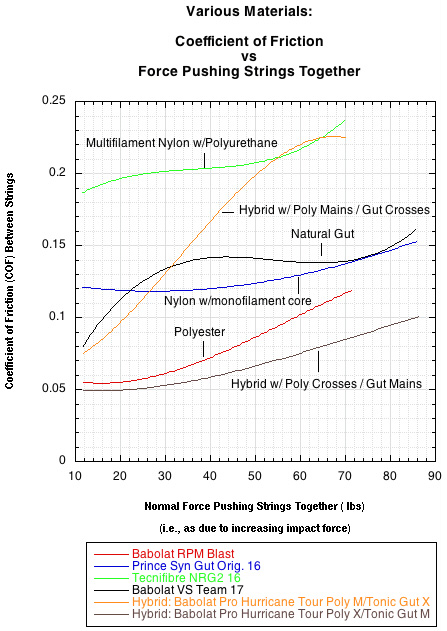
Figure 2 — COF vs Normal Force by string type.
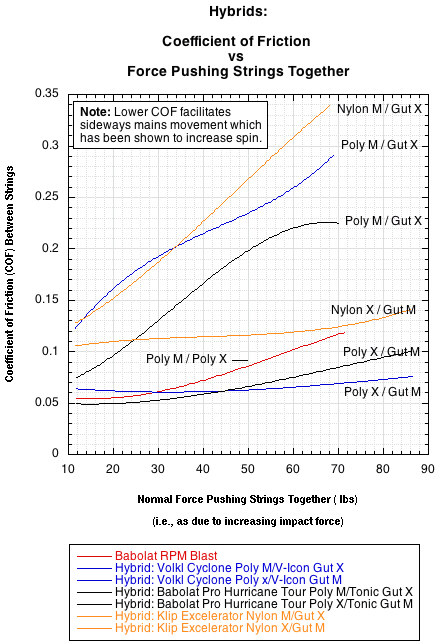
Figure 3 — COF vs Normal Force for hybrid combinations.
The COF tends to increase as the force pushing the strings together increases. This increase occurs at different rates depending on the material. Therefore, the graphs of two strings may cross, indicating a change in their relative slipperiness as the force changes. A very high speed impact may produce a normal force in the neighborhood of 250 pounds, but most topspin shots for most players will be around 150 pounds. If this force is distributed equally between 5 crosses and 5 mains (it isn't but the assumption is good enough for approximation), then each string will experience a force of about 15 pounds (however individual strings will experience more or less than this). So, the most relevant area in the graph to compare strings is around 15 pounds.
It is very interesting that the hybrid with poly crosses and gut mains is the combination with the lowest static COF. What is equally interesting is that if you change the combination to gut crosses and polyester mains, the static coefficient of friction is among the highest. Two hypotheses arise to explain these. First, if the cross is softer than the main, the main will sink into the cross. To initiate movement along the cross, the main will first have to climb a hill out of the valley it sits in, but also it will have to continually plow its way forward as it moves and sinks down the length of the cross. If the main is softer than the cross, it will deform over the cross such that it forms a slot or groove to move over the cross. That may actually facilitate movement, especially if the deformation causes a leakage of some oil, lubricant, etc. from inside the string. Second, if the cross is a multifilament or multistrand string like gut, it can also fray and break filaments as the polyester main moves up and down over its length. These broken filaments can stick up as obstacles, hooks, or spikes that can prevent or slow movement over them.
The following table lists the static COF for a number of individual strings and hybrids at a normal force of about 13 pounds at each string intersection and sorted by COF (more will be listed as they are tested).
| Static Coefficient of Friction (COF) | |||
|---|---|---|---|
| Company | String | Material | Static COF (13 lbs Normal Force) |
| Volkl | V-Fuse 16 | Hybrid: Poly X/Gut M | 0.063 |
| Hybrid | Babolat Tonic + 1.35 & Pro Hurricane Tour 17 | Hybrid: Poly X/Gut M | 0.066 |
| Babolat | RPM Blast | Polyester | 0.089 |
| Polyfibre | TCS 1.25 | Polyester | 0.098 |
| MSV | Focus EVO 1.25 | Polyester | 0.098 |
| Signum Pro | Poly Plasma Pure 1.23 | Polyester | 0.106 |
| Weiss Cannon | Silverstring 1.25 | Polyester | 0.108 |
| Tecnifibre | Pro Red Code 17 | Polyester | 0.109 |
| Babolat | Pro Hurricane Tour 17 | Polyester | 0.109 |
| Weiss Cannon | Turbotwist 1.18 | Polyester | 0.117 |
| Klip | Lightning 16 | Hybrid: Nylon X/Gut M | 0.117 |
| Tecnifibre | Black Code 17 | Polyester | 0.118 |
| Kirschbaum | Spiky Shark 1.25 | Polyester | 0.118 |
| Prince | Synthetic Gut Original 16 | Nylon | 0.124 |
| Luxilon | Alu Power Rough 16L | Polyester | 0.127 |
| Gamma | Zo Power 16L | Polyester | 0.132 |
| Signum Pro | Tornado 1.23 | Polyester | 0.139 |
| Gosen | OG-Sheep Micro Super 16L | Nylon | 0.145 |
| Babolat | VS Team 17 | Gut | 0.147 |
| Babolat | Addiction 16 | Nylon | 0.150 |
| Hybrid | Babolat Pro Hurricane Tour 17 & Tonic + 1.35 | Hybrid: Poly M/Gut X | 0.201 |
| Tecnifibre | NRG2 16 | Nylon | 0.208 |
| Volkl | V-Fuse 16 | Hybrid: Poly M/Gut X | 0.236 |
| Tecnifibre | TGV 1.30 | Nylon | 0.239 |
| Klip | Lightning 16 | Hybrid: Nylon M/Gut X | 0.268 |
| Tecnifibre | X-One Biphase 16 | Nylon | 0.314 |

